Tracking Changing Probabilities via Dynamic Learners

Consider a predictor, a learner, whose input is a stream of discrete items. The predictor's task, at every time point, is probabilistic multiclass prediction, i.e., to predict which item may occur next by outputting zero or more candidate items, each with a probability, after which the actual item is revealed and the predictor learns from this observation. To output probabilities, the predictor keeps track of the proportions of the items it has seen. The predictor has constant (limited) space and we seek efficient prediction and update techniques: The stream is unbounded, the set of items is unknown to the predictor and their totality can also grow unbounded. Moreover, there is non-stationarity: the underlying frequencies of items may change, substantially, from time to time. For instance, new items may start appearing and a few currently frequent items may cease to occur again. The predictor, being space-bounded, need only provide probabilities for those items with (currently) sufficiently high frequency, i.e., the salient items. This problem is motivated in the setting of prediction games, a self-supervised learning regime where concepts serve as both the predictors and the predictands, and the set of concepts grows over time, resulting in non-stationarities as new concepts are generated and used. We develop moving average techniques designed to respond to such non-stationarities in a timely manner, and explore their properties. One is a simple technique based on queuing of count snapshots, and another is a combination of queuing together with an extended version of sparse EMA. The latter combination supports predictand-specific dynamic learning rates. We find that this flexibility allows for a more accurate and timely convergence.

Expedition: A System for the Unsupervised Learning of a Hierarchy of Concepts

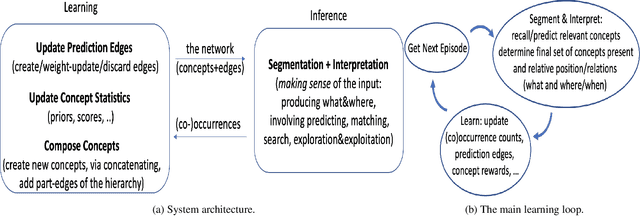
We present a system for bottom-up cumulative learning of myriad concepts corresponding to meaningful character strings, and their part-related and prediction edges. The learning is self-supervised in that the concepts discovered are used as predictors as well as targets of prediction. We devise an objective for segmenting with the learned concepts, derived from comparing to a baseline prediction system, that promotes making and using larger concepts, which in turn allows for predicting larger spans of text, and we describe a simple technique to promote exploration, i.e. trying out newly generated concepts in the segmentation process. We motivate and explain a layering of the concepts, to help separate the (conditional) distributions learnt among concepts. The layering of the concepts roughly corresponds to a part-whole concept hierarchy. With rudimentary segmentation and learning algorithms, the system is promising in that it acquires many concepts (tens of thousands in our small-scale experiments), and it learns to segment text well: when fed with English text with spaces removed, starting at the character level, much of what is learned respects word or phrase boundaries, and over time the average number of "bad" splits within segmentations, i.e. splits inside words, decreases as larger concepts are discovered and the system learns when to use them during segmentation. We report on promising experiments when the input text is converted to binary and the system begins with only two concepts, "0" and "1". The system is transparent, in the sense that it is easy to tell what the concepts learned correspond to, and which ones are active in a segmentation, or how the system "sees" its input. We expect this framework to be extensible and we discuss the current limitations and a number of directions for enhancing the learning and inference capabilities.

Binomial Tails for Community Analysis

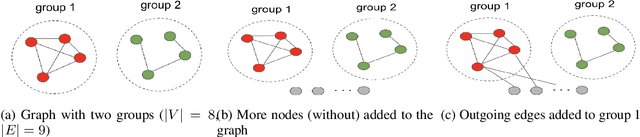
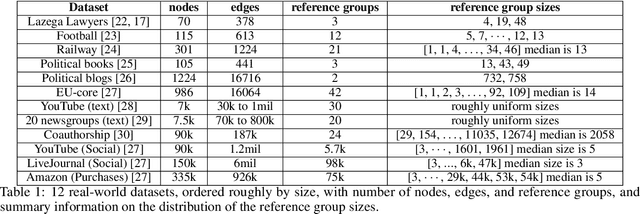
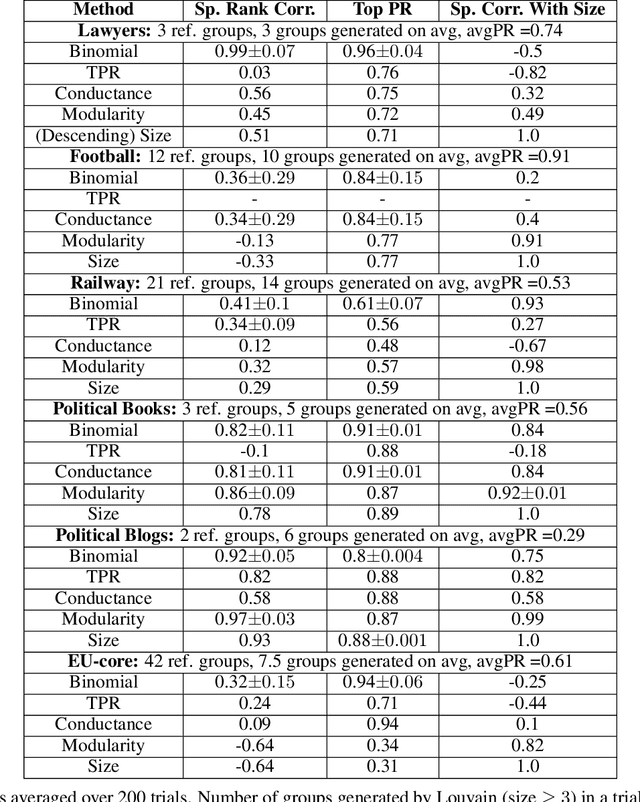
An important task of community discovery in networks is assessing significance of the results and robust ranking of the generated candidate groups. Often in practice, numerous candidate communities are discovered, and focusing the analyst's time on the most salient and promising findings is crucial. We develop simple efficient group scoring functions derived from tail probabilities using binomial models. Experiments on synthetic and numerous real-world data provides evidence that binomial scoring leads to a more robust ranking than other inexpensive scoring functions, such as conductance. Furthermore, we obtain confidence values ($p$-values) that can be used for filtering and labeling the discovered groups. Our analyses shed light on various properties of the approach. The binomial tail is simple and versatile, and we describe two other applications for community analysis: degree of community membership (which in turn yields group-scoring functions), and the discovery of significant edges in the community-induced graph.

Polynomial Value Iteration Algorithms for Detrerminstic MDPs

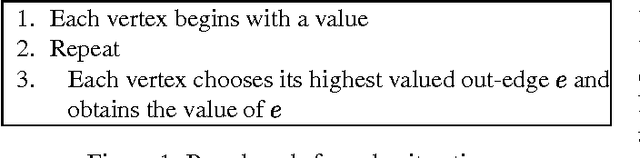
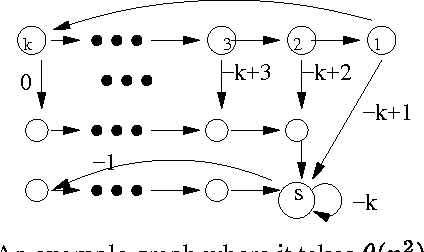
Value iteration is a commonly used and empirically competitive method in solving many Markov decision process problems. However, it is known that value iteration has only pseudo-polynomial complexity in general. We establish a somewhat surprising polynomial bound for value iteration on deterministic Markov decision (DMDP) problems. We show that the basic value iteration procedure converges to the highest average reward cycle on a DMDP problem in heta(n^2) iterations, or heta(mn^2) total time, where n denotes the number of states, and m the number of edges. We give two extensions of value iteration that solve the DMDP in heta(mn) time. We explore the analysis of policy iteration algorithms and report on an empirical study of value iteration showing that its convergence is much faster on random sparse graphs.

Budgeted Learning of Naive-Bayes Classifiers

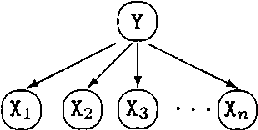
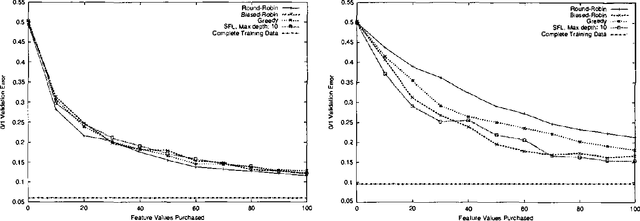
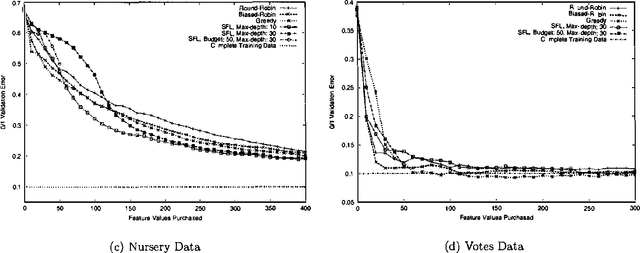
Frequently, acquiring training data has an associated cost. We consider the situation where the learner may purchase data during training, subject TO a budget. IN particular, we examine the CASE WHERE each feature label has an associated cost, AND the total cost OF ALL feature labels acquired during training must NOT exceed the budget.This paper compares methods FOR choosing which feature label TO purchase next, given the budget AND the CURRENT belief state OF naive Bayes model parameters.Whereas active learning has traditionally focused ON myopic(greedy) strategies FOR query selection, this paper presents a tractable method FOR incorporating knowledge OF the budget INTO the decision making process, which improves performance.

Active Model Selection

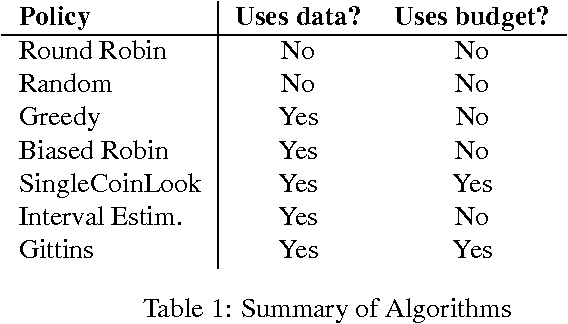
Classical learning assumes the learner is given a labeled data sample, from which it learns a model. The field of Active Learning deals with the situation where the learner begins not with a training sample, but instead with resources that it can use to obtain information to help identify the optimal model. To better understand this task, this paper presents and analyses the simplified "(budgeted) active model selection" version, which captures the pure exploration aspect of many active learning problems in a clean and simple problem formulation. Here the learner can use a fixed budget of "model probes" (where each probe evaluates the specified model on a random indistinguishable instance) to identify which of a given set of possible models has the highest expected accuracy. Our goal is a policy that sequentially determines which model to probe next, based on the information observed so far. We present a formal description of this task, and show that it is NPhard in general. We then investigate a number of algorithms for this task, including several existing ones (eg, "Round-Robin", "Interval Estimation", "Gittins") as well as some novel ones (e.g., "Biased-Robin"), describing first their approximation properties and then their empirical performance on various problem instances. We observe empirically that the simple biased-robin algorithm significantly outperforms the other algorithms in the case of identical costs and priors.

An Empirical Comparison of Algorithms for Aggregating Expert Predictions

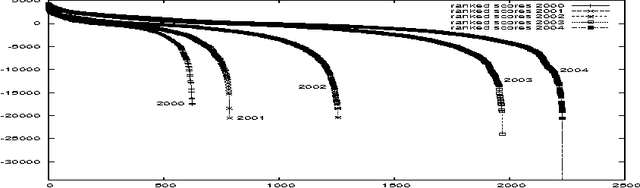
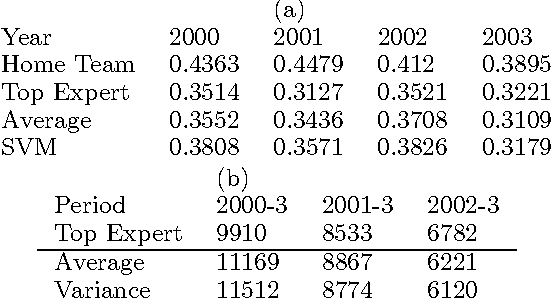
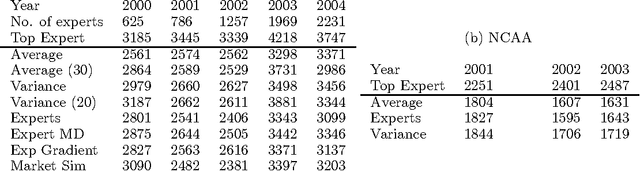
Predicting the outcomes of future events is a challenging problem for which a variety of solution methods have been explored and attempted. We present an empirical comparison of a variety of online and offline adaptive algorithms for aggregating experts' predictions of the outcomes of five years of US National Football League games (1319 games) using expert probability elicitations obtained from an Internet contest called ProbabilitySports. We find that it is difficult to improve over simple averaging of the predictions in terms of prediction accuracy, but that there is room for improvement in quadratic loss. Somewhat surprisingly, a Bayesian estimation algorithm which estimates the variance of each expert's prediction exhibits the most consistent superior performance over simple averaging among our collection of algorithms.