Active Model Selection
Paper and Code
Jul 11, 2012
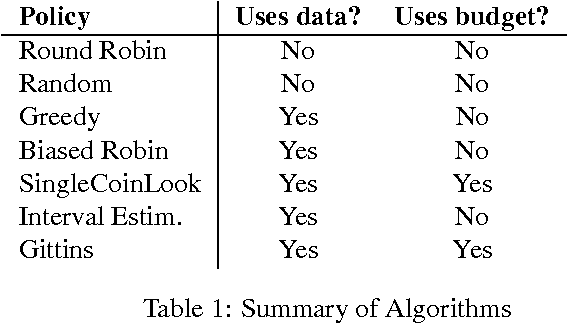

Classical learning assumes the learner is given a labeled data sample, from which it learns a model. The field of Active Learning deals with the situation where the learner begins not with a training sample, but instead with resources that it can use to obtain information to help identify the optimal model. To better understand this task, this paper presents and analyses the simplified "(budgeted) active model selection" version, which captures the pure exploration aspect of many active learning problems in a clean and simple problem formulation. Here the learner can use a fixed budget of "model probes" (where each probe evaluates the specified model on a random indistinguishable instance) to identify which of a given set of possible models has the highest expected accuracy. Our goal is a policy that sequentially determines which model to probe next, based on the information observed so far. We present a formal description of this task, and show that it is NPhard in general. We then investigate a number of algorithms for this task, including several existing ones (eg, "Round-Robin", "Interval Estimation", "Gittins") as well as some novel ones (e.g., "Biased-Robin"), describing first their approximation properties and then their empirical performance on various problem instances. We observe empirically that the simple biased-robin algorithm significantly outperforms the other algorithms in the case of identical costs and priors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge