Binomial Tails for Community Analysis
Paper and Code
Dec 17, 2020
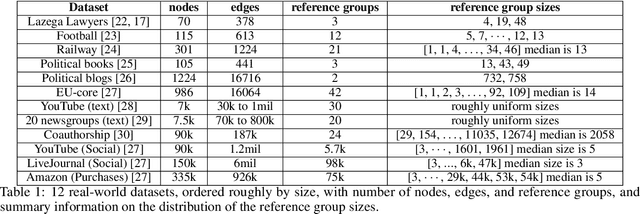

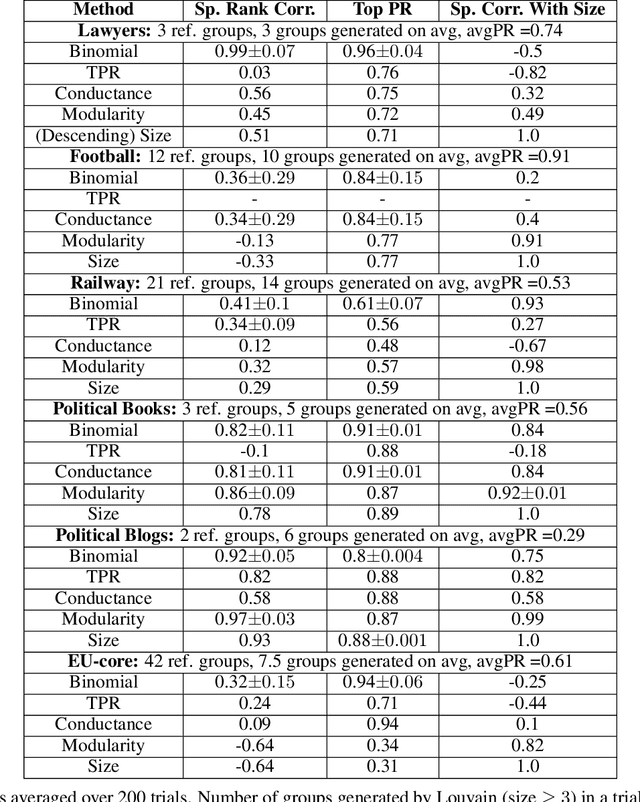
An important task of community discovery in networks is assessing significance of the results and robust ranking of the generated candidate groups. Often in practice, numerous candidate communities are discovered, and focusing the analyst's time on the most salient and promising findings is crucial. We develop simple efficient group scoring functions derived from tail probabilities using binomial models. Experiments on synthetic and numerous real-world data provides evidence that binomial scoring leads to a more robust ranking than other inexpensive scoring functions, such as conductance. Furthermore, we obtain confidence values ($p$-values) that can be used for filtering and labeling the discovered groups. Our analyses shed light on various properties of the approach. The binomial tail is simple and versatile, and we describe two other applications for community analysis: degree of community membership (which in turn yields group-scoring functions), and the discovery of significant edges in the community-induced graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge