Omer Dror
Unsupervised Ensemble Regression
Mar 08, 2017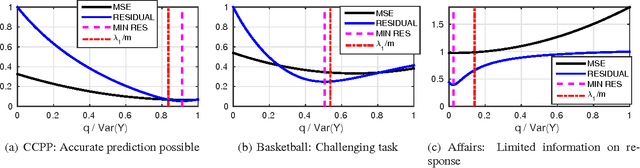
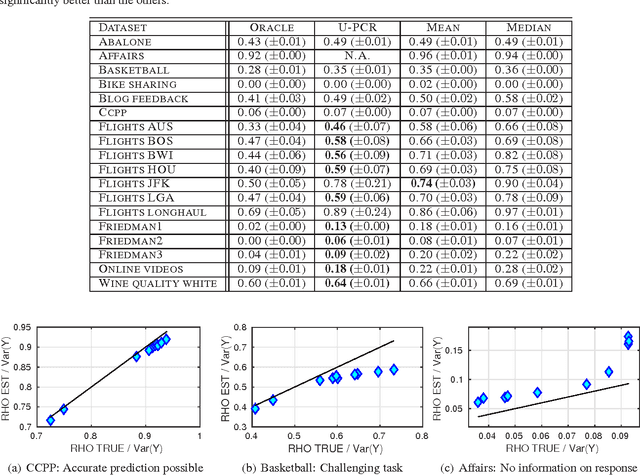
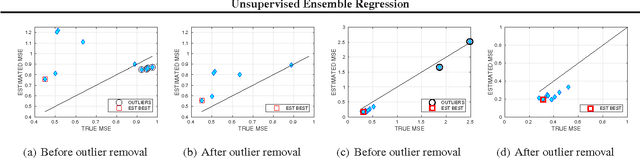
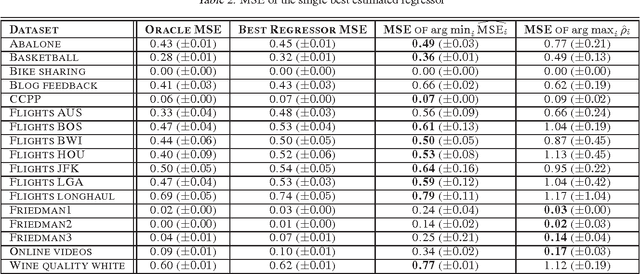
Abstract:Consider a regression problem where there is no labeled data and the only observations are the predictions $f_i(x_j)$ of $m$ experts $f_{i}$ over many samples $x_j$. With no knowledge on the accuracy of the experts, is it still possible to accurately estimate the unknown responses $y_{j}$? Can one still detect the least or most accurate experts? In this work we propose a framework to study these questions, based on the assumption that the $m$ experts have uncorrelated deviations from the optimal predictor. Assuming the first two moments of the response are known, we develop methods to detect the best and worst regressors, and derive U-PCR, a novel principal components approach for unsupervised ensemble regression. We provide theoretical support for U-PCR and illustrate its improved accuracy over the ensemble mean and median on a variety of regression problems.
A Deep Learning Approach to Unsupervised Ensemble Learning
Feb 06, 2016
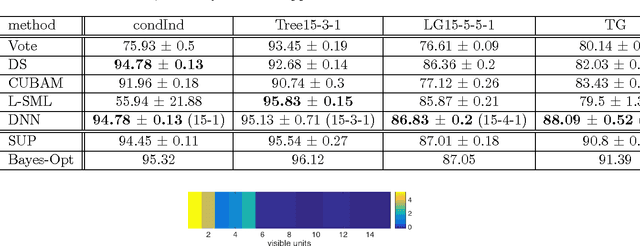
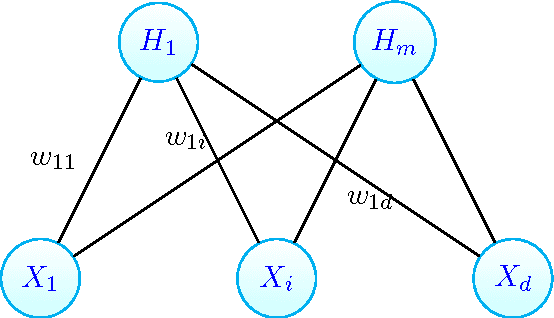
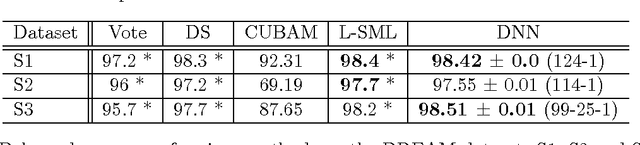
Abstract:We show how deep learning methods can be applied in the context of crowdsourcing and unsupervised ensemble learning. First, we prove that the popular model of Dawid and Skene, which assumes that all classifiers are conditionally independent, is {\em equivalent} to a Restricted Boltzmann Machine (RBM) with a single hidden node. Hence, under this model, the posterior probabilities of the true labels can be instead estimated via a trained RBM. Next, to address the more general case, where classifiers may strongly violate the conditional independence assumption, we propose to apply RBM-based Deep Neural Net (DNN). Experimental results on various simulated and real-world datasets demonstrate that our proposed DNN approach outperforms other state-of-the-art methods, in particular when the data violates the conditional independence assumption.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge