Unsupervised Ensemble Regression
Paper and Code
Mar 08, 2017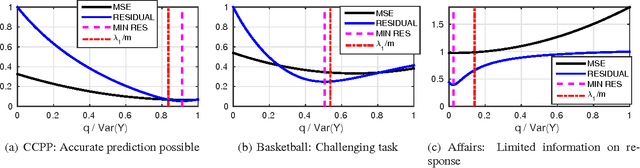
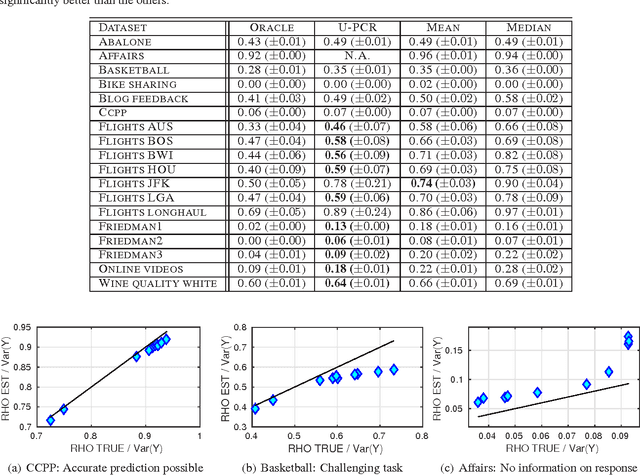
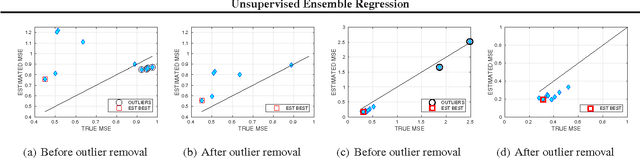
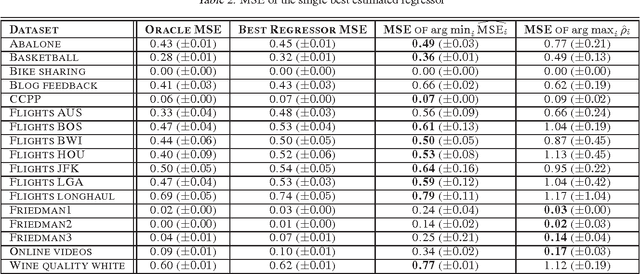
Consider a regression problem where there is no labeled data and the only observations are the predictions $f_i(x_j)$ of $m$ experts $f_{i}$ over many samples $x_j$. With no knowledge on the accuracy of the experts, is it still possible to accurately estimate the unknown responses $y_{j}$? Can one still detect the least or most accurate experts? In this work we propose a framework to study these questions, based on the assumption that the $m$ experts have uncorrelated deviations from the optimal predictor. Assuming the first two moments of the response are known, we develop methods to detect the best and worst regressors, and derive U-PCR, a novel principal components approach for unsupervised ensemble regression. We provide theoretical support for U-PCR and illustrate its improved accuracy over the ensemble mean and median on a variety of regression problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge