Subspace Track-before-Detect for Passive Multi-Target Tracking with Unknown Emitted Signals

Passive multi-target tracking (MTT) aims to infer the kinematic states of multiple targets from noisy sensor data in which contributions from unknown target-emitted signals are superposed. Track-before-detect (TBD) methods improve robustness to noise by operating directly on raw sensor data without relying on a preceding detection stage. However, many existing TBD methods assume that each target's contribution to the sensor data is determined solely by its kinematic state. This assumption limits their applicability to passive MTT, where each target's contribution depends on both its kinematic state and the unknown emitted signal. We propose subspace TBD, a passive multi-target TBD method based on a likelihood derived from the complex Bingham distribution that does not require explicit modeling or estimation of the unknown emitted signals. In a particle filter (PF) framework, each multi-target hypothesis is mapped to a low-dimensional subspace spanned by the steering vectors corresponding to the hypothesized target states. The likelihood is then used to evaluate the alignment of the normalized multichannel sensor data with this subspace. Preliminary experiments with simulated acoustic measurements and a given target activity pattern show that the proposed method can track two moving targets emitting unknown signals at a signal-to-noise ratio (SNR) of -10dB, whereas a conventional TBD baseline yields substantially larger tracking errors.

cSTMM: A Unified Complex Spherical Student's $t$ Mixture Model for Directional Statistics in Mask-Based Blind Speech Separation

Mask-based blind speech separation (BSS) estimates source-wise time-frequency (TF) masks by clustering multichannel observations using spatial information. The directional statistical approach clusters normalized multichannel observations on the complex unit sphere, without explicitly extracting phase and level difference features based on the plane-wave or spherical-wave assumptions. However, prior studies have mostly compared a small number of separately defined directional statistical mixture models, whereas a broader distribution family would enable a more systematic study of how density profiles affect separation performance. We propose the complex spherical Student's t mixture model (cSTMM), a directional mixture model that connects the complex angular central Gaussian mixture model (cACGMM), complex Bingham mixture model (cBMM), and complex Watson mixture model (cWMM) through the degrees-of-freedom parameter $ν$. We also derive a generalized minorization-maximization (MM) based procedure for parameter estimation. A no-restart evaluation on noise-free LibriSpeech mixtures reverberated with measured room impulse responses shows that a single development-selected value $ν^\ast=1$ achieved higher test-set mean signal-to-distortion ratio improvements (SDRi) than the cACGMM-equivalent setting $ν=M$ in all acoustic conditions, with an average condition-wise gain of 0.25dB. The experiments also numerically verify that the proposed formulation numerically recovers the cACGMM, cBMM, and cWMM cases.

Fast Multichannel NMF with Block-Diagonal Spatial Covariance Matrices for Efficient Blind Source Separation Using Distributed Microphone Arrays

Distributed microphone arrays composed of multiple subarrays enable blind source separation over a wide spatial area. Directly applying fast multichannel nonnegative matrix factorization (FastMNMF) to all subarrays can exploit observations from all subarrays, but it requires repeated inversions of large matrices spanning all microphones, causing the computational cost to increase rapidly as the number of microphones grows. In contrast, applying FastMNMF to one subarray reduces the matrix size but cannot exploit observations from other subarrays. We propose distributed FastMNMF, which imposes a block-diagonal structure on the source spatial covariance matrices, so that matrix inversions are performed within subarrays. The NMF-based source spectrogram model is shared across subarrays, allowing the method to aggregate source activity information while discarding inter-subarray covariance. In synchronized, noiseless simulations with fixed room and array/source geometry, the method required less computation time than conventional FastMNMF using all subarrays, achieved a higher average source-to-distortion ratio than conventional FastMNMF using one subarray, and was applicable in the tested five-source condition, where each four-microphone subarray was locally underdetermined.

30+ Years of Source Separation Research: Achievements and Future Challenges

Source separation (SS) of acoustic signals is a research field that emerged in the mid-1990s and has flourished ever since. On the occasion of ICASSP's 50th anniversary, we review the major contributions and advancements in the past three decades in the speech, audio, and music SS research field. We will cover both single- and multi-channel SS approaches. We will also look back on key efforts to foster a culture of scientific evaluation in the research field, including challenges, performance metrics, and datasets. We will conclude by discussing current trends and future research directions.

Audio Signal Enhancement with Learning from Positive and Unlabelled Data

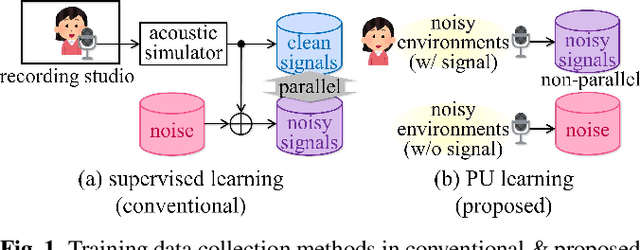
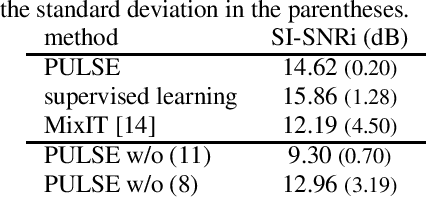
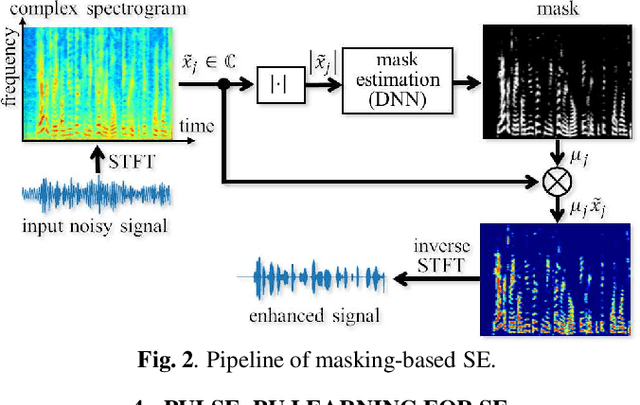
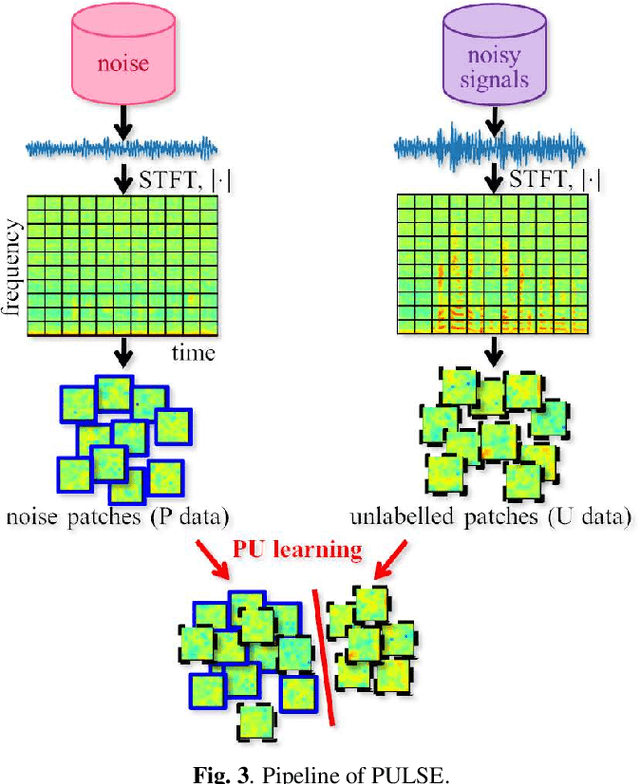
Supervised learning is a mainstream approach to audio signal enhancement (SE) and requires parallel training data consisting of both noisy signals and the corresponding clean signals. Such data can only be synthesised and are thus mismatched with real data, which can result in poor performance. Moreover, it is often difficult/impossible to obtain clean signals, making it difficult/impossible to apply the approach in this case. Here we explore SE using non-parallel training data consisting of noisy signals and noise, which can be easily recorded. We define the positive (P) and the negative (N) classes as signal absence and presence, respectively. We observe that the spectrogram patches of noise clips can be used as P data and those of noisy signal clips as unlabelled data. Thus, learning from positive and unlabelled data enables a convolutional neural network to learn to classify each spectrogram patch as P or N for SE.

A Joint Diagonalization Based Efficient Approach to Underdetermined Blind Audio Source Separation Using the Multichannel Wiener Filter

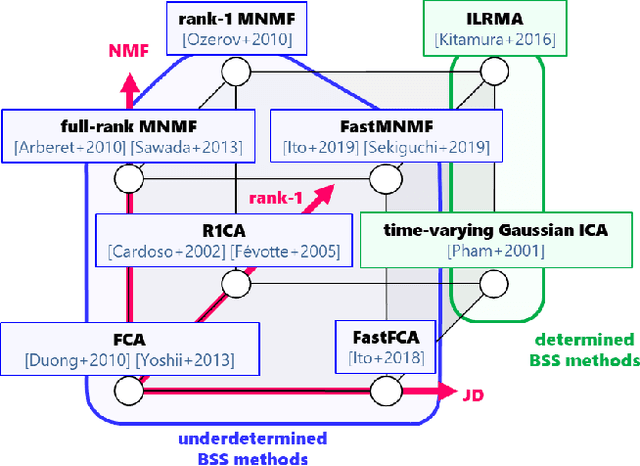
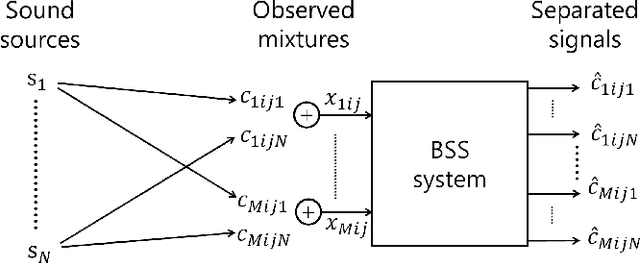
This paper presents a computationally efficient approach to blind source separation (BSS) of audio signals, applicable even when there are more sources than microphones (i.e., the underdetermined case). When there are as many sources as microphones (i.e., the determined case), BSS can be performed computationally efficiently by independent component analysis (ICA). Unfortunately, however, ICA is basically inapplicable to the underdetermined case. Another BSS approach using the multichannel Wiener filter (MWF) is applicable even to this case, and encompasses full-rank spatial covariance analysis (FCA) and multichannel non-negative matrix factorization (MNMF). However, these methods require massive numbers of matrix inversions to design the MWF, and are thus computationally inefficient. To overcome this drawback, we exploit the well-known property of diagonal matrices that matrix inversion amounts to mere inversion of the diagonal elements and can thus be performed computationally efficiently. This makes it possible to drastically reduce the computational cost of the above matrix inversions based on a joint diagonalization (JD) idea, leading to computationally efficient BSS. Specifically, we restrict the N spatial covariance matrices (SCMs) of all N sources to a class of (exactly) jointly diagonalizable matrices. Based on this approach, we present FastFCA, a computationally efficient extension of FCA. We also present a unified framework for underdetermined and determined audio BSS, which highlights a theoretical connection between FastFCA and other methods. Moreover, we reveal that FastFCA can be regarded as a regularized version of approximate joint diagonalization (AJD).