A Joint Diagonalization Based Efficient Approach to Underdetermined Blind Audio Source Separation Using the Multichannel Wiener Filter
Paper and Code
Jan 21, 2021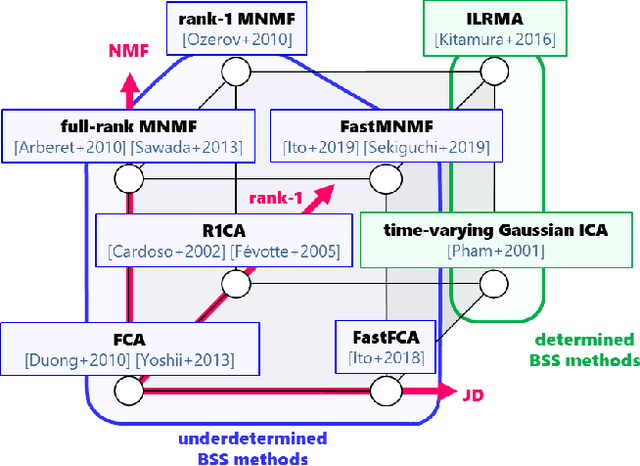
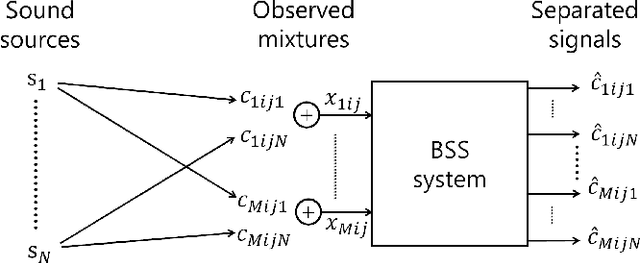

This paper presents a computationally efficient approach to blind source separation (BSS) of audio signals, applicable even when there are more sources than microphones (i.e., the underdetermined case). When there are as many sources as microphones (i.e., the determined case), BSS can be performed computationally efficiently by independent component analysis (ICA). Unfortunately, however, ICA is basically inapplicable to the underdetermined case. Another BSS approach using the multichannel Wiener filter (MWF) is applicable even to this case, and encompasses full-rank spatial covariance analysis (FCA) and multichannel non-negative matrix factorization (MNMF). However, these methods require massive numbers of matrix inversions to design the MWF, and are thus computationally inefficient. To overcome this drawback, we exploit the well-known property of diagonal matrices that matrix inversion amounts to mere inversion of the diagonal elements and can thus be performed computationally efficiently. This makes it possible to drastically reduce the computational cost of the above matrix inversions based on a joint diagonalization (JD) idea, leading to computationally efficient BSS. Specifically, we restrict the N spatial covariance matrices (SCMs) of all N sources to a class of (exactly) jointly diagonalizable matrices. Based on this approach, we present FastFCA, a computationally efficient extension of FCA. We also present a unified framework for underdetermined and determined audio BSS, which highlights a theoretical connection between FastFCA and other methods. Moreover, we reveal that FastFCA can be regarded as a regularized version of approximate joint diagonalization (AJD).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge