Neural Lyapunov Control

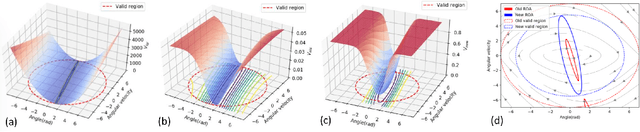
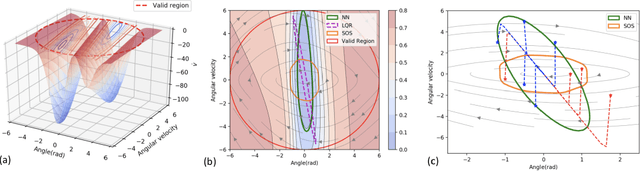
We propose new methods for learning control policies and neural network Lyapunov functions for nonlinear control problems, with provable guarantee of stability. The framework consists of a learner that attempts to find the control and Lyapunov functions, and a falsifier that finds counterexamples to quickly guide the learner towards solutions. The procedure terminates when no counterexample is found by the falsifier, in which case the controlled nonlinear system is provably stable. The approach significantly simplifies the process of Lyapunov control design, provides end-to-end correctness guarantee, and can obtain much larger regions of attraction than existing methods such as LQR and SOS/SDP. We show experiments on how the new methods obtain high-quality solutions for challenging control problems.

Statistically Model Checking PCTL Specifications on Markov Decision Processes via Reinforcement Learning

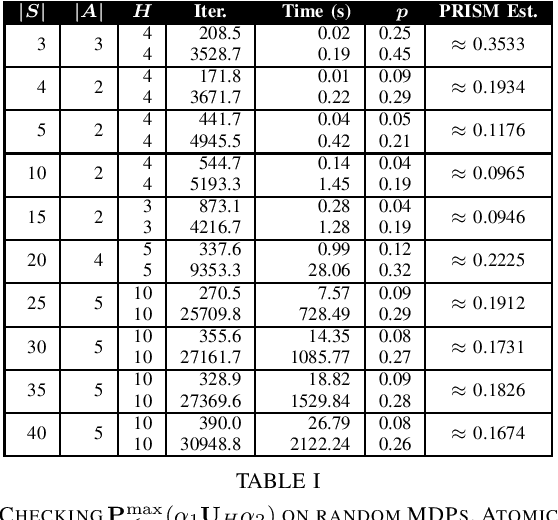
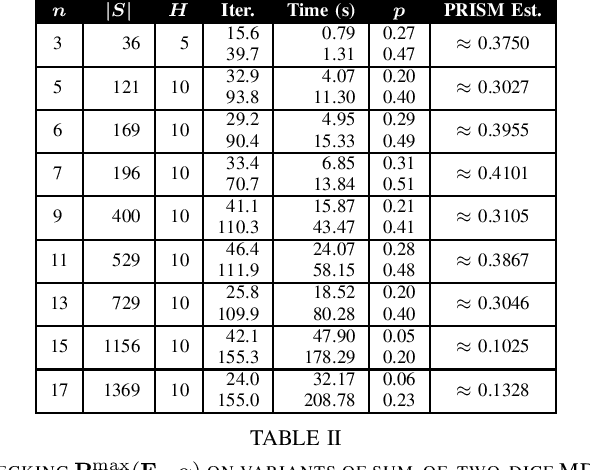
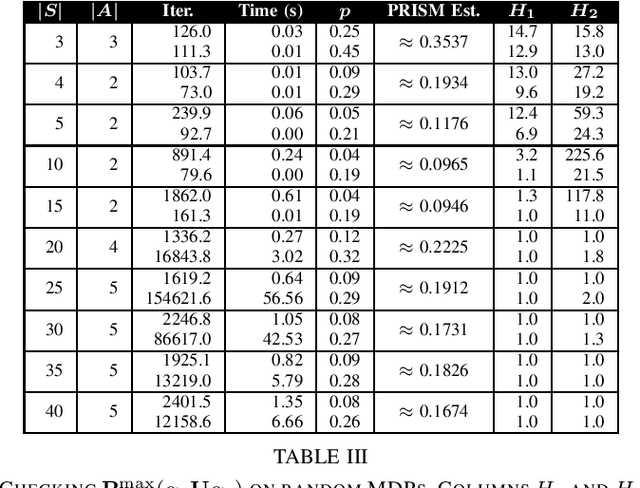
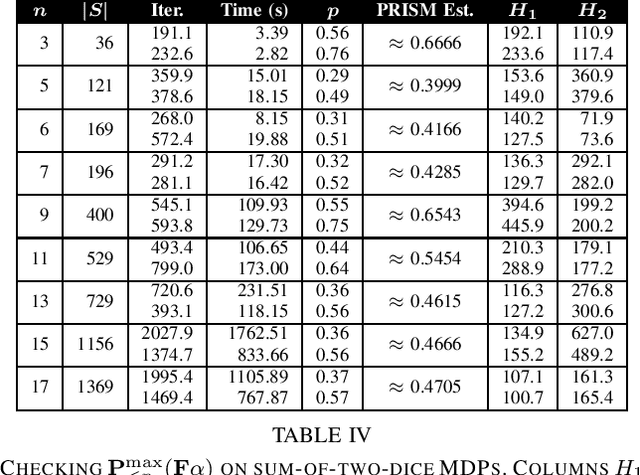
Probabilistic Computation Tree Logic (PCTL) is frequently used to formally specify control objectives such as probabilistic reachability and safety. In this work, we focus on model checking PCTL specifications statistically on Markov Decision Processes (MDPs) by sampling, e.g., checking whether there exists a feasible policy such that the probability of reaching certain goal states is greater than a threshold. We use reinforcement learning to search for such a feasible policy for PCTL specifications, and then develop a statistical model checking (SMC) method with provable guarantees on its error. Specifically, we first use upper-confidence-bound (UCB) based Q-learning to design an SMC algorithm for bounded-time PCTL specifications, and then extend this algorithm to unbounded-time specifications by identifying a proper truncation time by checking the PCTL specification and its negation at the same time. Finally, we evaluate the proposed method on case studies.

Self-Driving Vehicle Verification Towards a Benchmark

Industrial cyber-physical systems are hybrid systems with strict safety requirements. Despite not having a formal semantics, most of these systems are modeled using Stateflow/Simulink for mainly two reasons: (1) it is easier to model, test, and simulate using these tools, and (2) dynamics of these systems are not supported by most other tools. Furthermore, with the ever growing complexity of cyber-physical systems, grows the gap between what can be modeled using an automatic formal verification tool and models of industrial cyber-physical systems. In this paper, we present a simple formal model for self-deriving cars. While after some simplification, safety of this system has already been proven manually, to the best of our knowledge, no automatic formal verification tool supports its dynamics. We hope this serves as a challenge problem for formal verification tools targeting industrial applications.