Convergence of Gradient-based MAML in LQR

The main objective of this research paper is to investigate the local convergence characteristics of Model-agnostic Meta-learning (MAML) when applied to linear system quadratic optimal control (LQR). MAML and its variations have become popular techniques for quickly adapting to new tasks by leveraging previous learning knowledge in areas like regression, classification, and reinforcement learning. However, its theoretical guarantees remain unknown due to non-convexity and its structure, making it even more challenging to ensure stability in the dynamic system setting. This study focuses on exploring MAML in the LQR setting, providing its local convergence guarantees while maintaining the stability of the dynamical system. The paper also presents simple numerical results to demonstrate the convergence properties of MAML in LQR tasks.

Statistically Model Checking PCTL Specifications on Markov Decision Processes via Reinforcement Learning

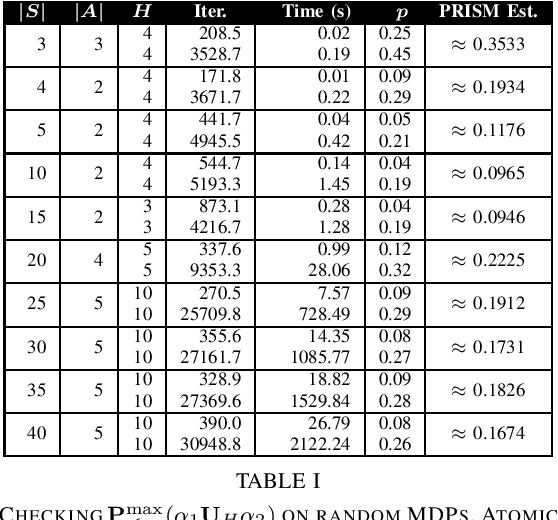
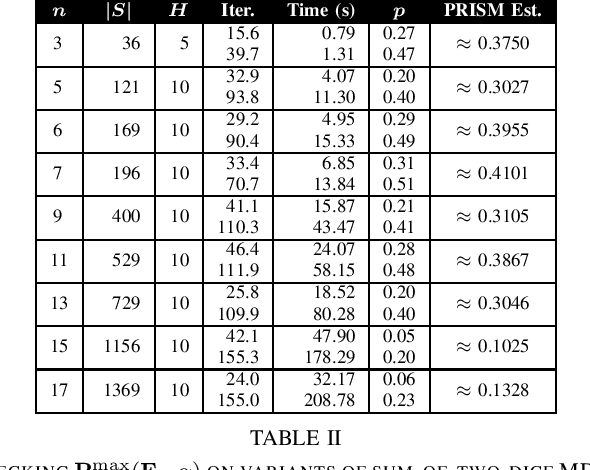
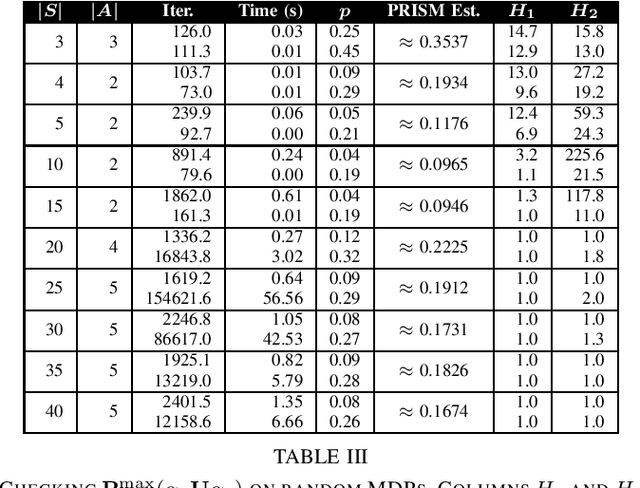
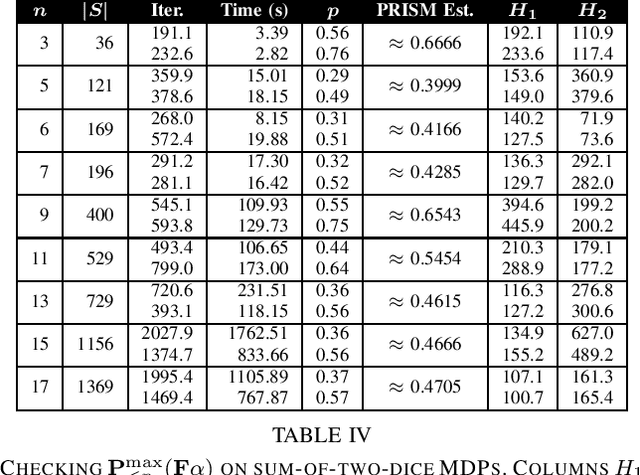
Probabilistic Computation Tree Logic (PCTL) is frequently used to formally specify control objectives such as probabilistic reachability and safety. In this work, we focus on model checking PCTL specifications statistically on Markov Decision Processes (MDPs) by sampling, e.g., checking whether there exists a feasible policy such that the probability of reaching certain goal states is greater than a threshold. We use reinforcement learning to search for such a feasible policy for PCTL specifications, and then develop a statistical model checking (SMC) method with provable guarantees on its error. Specifically, we first use upper-confidence-bound (UCB) based Q-learning to design an SMC algorithm for bounded-time PCTL specifications, and then extend this algorithm to unbounded-time specifications by identifying a proper truncation time by checking the PCTL specification and its negation at the same time. Finally, we evaluate the proposed method on case studies.

Differential Privacy for Sequential Algorithms

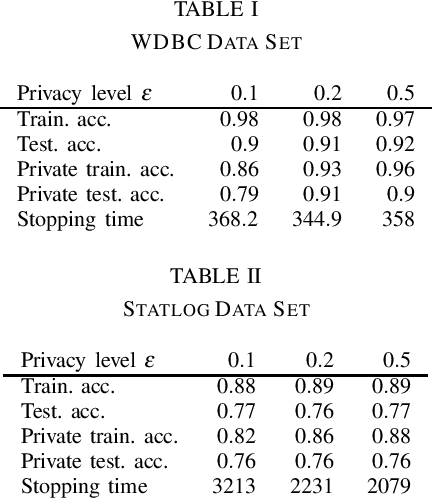
We study the differential privacy of sequential statistical inference and learning algorithms that are characterized by random termination time. Using the two examples: sequential probability ratio test and sequential empirical risk minimization, we show that the number of steps such algorithms execute before termination can jeopardize the differential privacy of the input data in a similar fashion as their outputs, and it is impossible to use the usual Laplace mechanism to achieve standard differentially private in these examples. To remedy this, we propose a notion of weak differential privacy and demonstrate its equivalence to the standard case for large i.i.d. samples. We show that using the Laplace mechanism, weak differential privacy can be achieved for both the sequential probability ratio test and the sequential empirical risk minimization with proper performance guarantees. Finally, we provide preliminary experimental results on the Breast Cancer Wisconsin (Diagnostic) and Landsat Satellite Data Sets from the UCI repository.