Incremental IVF Index Maintenance for Streaming Vector Search

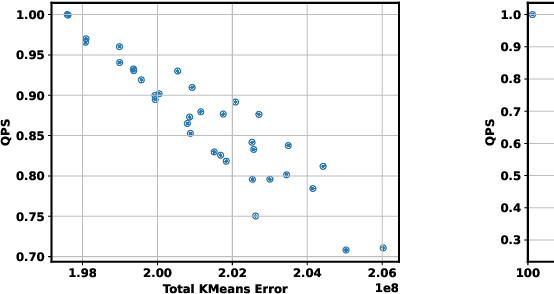
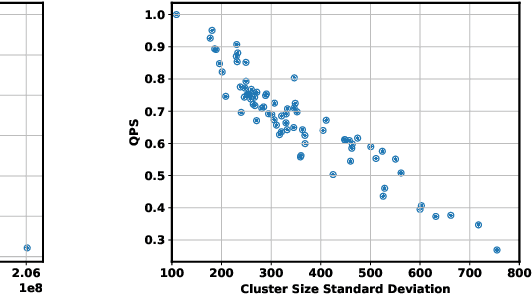
The prevalence of vector similarity search in modern machine learning applications and the continuously changing nature of data processed by these applications necessitate efficient and effective index maintenance techniques for vector search indexes. Designed primarily for static workloads, existing vector search indexes degrade in search quality and performance as the underlying data is updated unless costly index reconstruction is performed. To address this, we introduce Ada-IVF, an incremental indexing methodology for Inverted File (IVF) indexes. Ada-IVF consists of 1) an adaptive maintenance policy that decides which index partitions are problematic for performance and should be repartitioned and 2) a local re-clustering mechanism that determines how to repartition them. Compared with state-of-the-art dynamic IVF index maintenance strategies, Ada-IVF achieves an average of 2x and up to 5x higher update throughput across a range of benchmark workloads.

New Probabilistic Bounds on Eigenvalues and Eigenvectors of Random Kernel Matrices

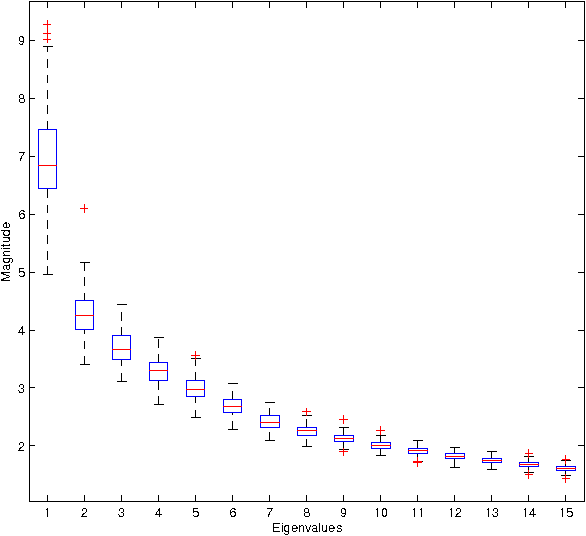
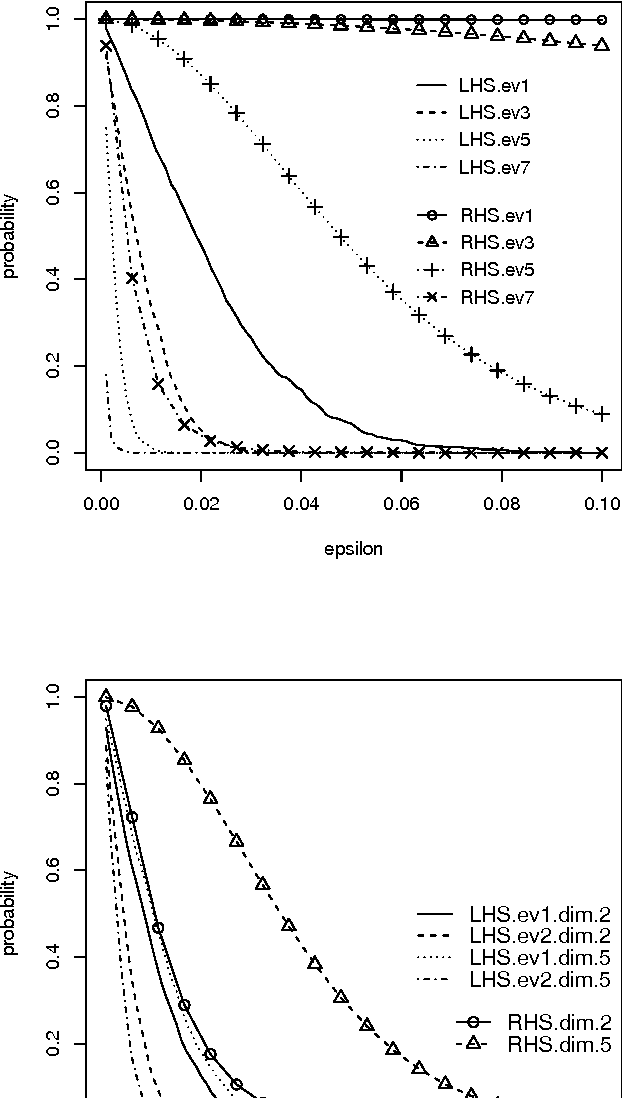
Kernel methods are successful approaches for different machine learning problems. This success is mainly rooted in using feature maps and kernel matrices. Some methods rely on the eigenvalues/eigenvectors of the kernel matrix, while for other methods the spectral information can be used to estimate the excess risk. An important question remains on how close the sample eigenvalues/eigenvectors are to the population values. In this paper, we improve earlier results on concentration bounds for eigenvalues of general kernel matrices. For distance and inner product kernel functions, e.g. radial basis functions, we provide new concentration bounds, which are characterized by the eigenvalues of the sample covariance matrix. Meanwhile, the obstacles for sharper bounds are accounted for and partially addressed. As a case study, we derive a concentration inequality for sample kernel target-alignment.