New Probabilistic Bounds on Eigenvalues and Eigenvectors of Random Kernel Matrices
Paper and Code
Feb 14, 2012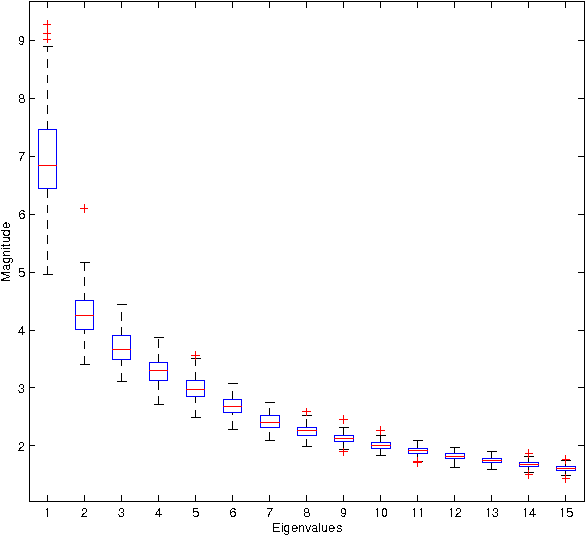
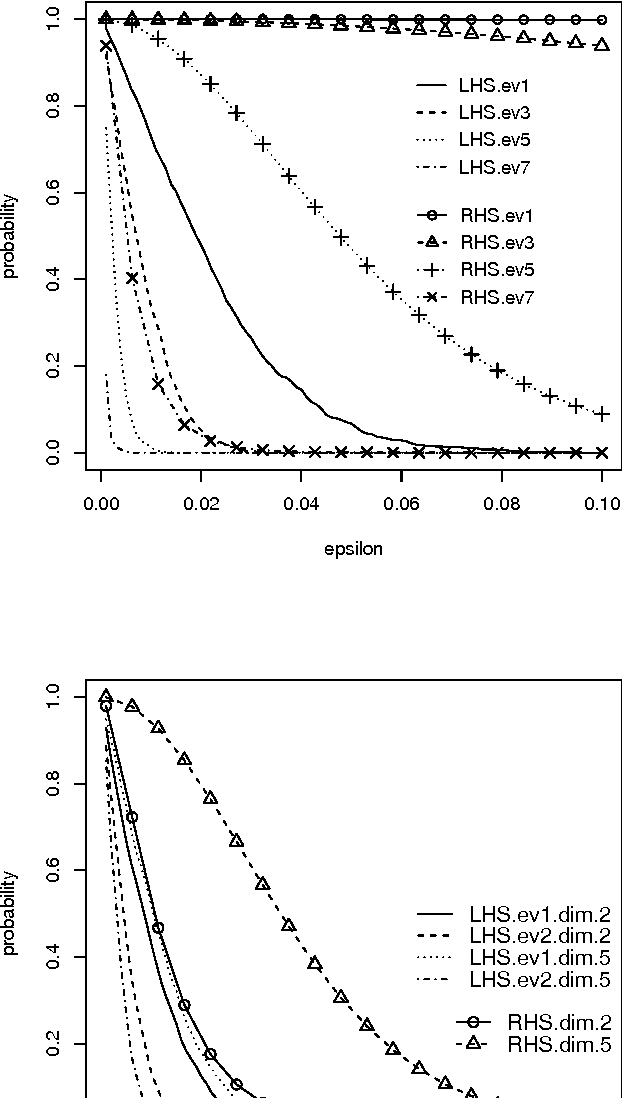
Kernel methods are successful approaches for different machine learning problems. This success is mainly rooted in using feature maps and kernel matrices. Some methods rely on the eigenvalues/eigenvectors of the kernel matrix, while for other methods the spectral information can be used to estimate the excess risk. An important question remains on how close the sample eigenvalues/eigenvectors are to the population values. In this paper, we improve earlier results on concentration bounds for eigenvalues of general kernel matrices. For distance and inner product kernel functions, e.g. radial basis functions, we provide new concentration bounds, which are characterized by the eigenvalues of the sample covariance matrix. Meanwhile, the obstacles for sharper bounds are accounted for and partially addressed. As a case study, we derive a concentration inequality for sample kernel target-alignment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge