PyEvalAI: AI-assisted evaluation of Jupyter Notebooks for immediate personalized feedback

Grading student assignments in STEM courses is a laborious and repetitive task for tutors, often requiring a week to assess an entire class. For students, this delay of feedback prevents iterating on incorrect solutions, hampers learning, and increases stress when exercise scores determine admission to the final exam. Recent advances in AI-assisted education, such as automated grading and tutoring systems, aim to address these challenges by providing immediate feedback and reducing grading workload. However, existing solutions often fall short due to privacy concerns, reliance on proprietary closed-source models, lack of support for combining Markdown, LaTeX and Python code, or excluding course tutors from the grading process. To overcome these limitations, we introduce PyEvalAI, an AI-assisted evaluation system, which automatically scores Jupyter notebooks using a combination of unit tests and a locally hosted language model to preserve privacy. Our approach is free, open-source, and ensures tutors maintain full control over the grading process. A case study demonstrates its effectiveness in improving feedback speed and grading efficiency for exercises in a university-level course on numerics.

Physics-guided Shape-from-Template: Monocular Video Perception through Neural Surrogate Models

3D reconstruction of dynamic scenes is a long-standing problem in computer graphics and increasingly difficult the less information is available. Shape-from-Template (SfT) methods aim to reconstruct a template-based geometry from RGB images or video sequences, often leveraging just a single monocular camera without depth information, such as regular smartphone recordings. Unfortunately, existing reconstruction methods are either unphysical and noisy or slow in optimization. To solve this problem, we propose a novel SfT reconstruction algorithm for cloth using a pre-trained neural surrogate model that is fast to evaluate, stable, and produces smooth reconstructions due to a regularizing physics simulation. Differentiable rendering of the simulated mesh enables pixel-wise comparisons between the reconstruction and a target video sequence that can be used for a gradient-based optimization procedure to extract not only shape information but also physical parameters such as stretching, shearing, or bending stiffness of the cloth. This allows to retain a precise, stable, and smooth reconstructed geometry while reducing the runtime by a factor of 400-500 compared to $\phi$-SfT, a state-of-the-art physics-based SfT approach.

Spline-PINN: Approaching PDEs without Data using Fast, Physics-Informed Hermite-Spline CNNs

Partial Differential Equations (PDEs) are notoriously difficult to solve. In general, closed-form solutions are not available and numerical approximation schemes are computationally expensive. In this paper, we propose to approach the solution of PDEs based on a novel technique that combines the advantages of two recently emerging machine learning based approaches. First, physics-informed neural networks (PINNs) learn continuous solutions of PDEs and can be trained with little to no ground truth data. However, PINNs do not generalize well to unseen domains. Second, convolutional neural networks provide fast inference and generalize but either require large amounts of training data or a physics-constrained loss based on finite differences that can lead to inaccuracies and discretization artifacts. We leverage the advantages of both of these approaches by using Hermite spline kernels in order to continuously interpolate a grid-based state representation that can be handled by a CNN. This allows for training without any precomputed training data using a physics-informed loss function only and provides fast, continuous solutions that generalize to unseen domains. We demonstrate the potential of our method at the examples of the incompressible Navier-Stokes equation and the damped wave equation. Our models are able to learn several intriguing phenomena such as Karman vortex streets, the Magnus effect, Doppler effect, interference patterns and wave reflections. Our quantitative assessment and an interactive real-time demo show that we are narrowing the gap in accuracy of unsupervised ML based methods to industrial CFD solvers while being orders of magnitude faster.

Fast Fluid Simulations in 3D with Physics-Informed Deep Learning

Physically plausible fluid simulations play an important role in modern computer graphics. However, in order to achieve real-time performance, computational speed needs to be traded-off with physical accuracy. Surrogate fluid models based on neural networks are a promising candidate to achieve both: fast fluid simulations and high physical accuracy. However, these approaches do not generalize to new fluid domains, rely on massive amounts of training data or require complex pipelines for training and inference. In this work, we present a 3D extension to our recently proposed fluid training framework, which addresses the aforementioned issues in 2D. Our method allows to train fluid models that generalize to new fluid domains without requiring fluid simulation data and simplifies the training and inference pipeline as the fluid models directly map a fluid state and boundary conditions at a moment t to a subsequent state at t+dt. To this end, we introduce a physics-informed loss function based on the residuals of the Navier-Stokes equations on a 3D staggered Marker-and-Cell grid. Furthermore, we propose an efficient 3D U-Net based architecture in order to cope with the high demands of 3D grids in terms of memory and computational complexity. Our method allows for real-time fluid simulations on a 128x64x64 grid that include various fluid phenomena such as the Magnus effect or Karman vortex streets, and generalize to domain geometries not considered during training. Our method indicates strong improvements in terms of accuracy, speed and generalization capabilities over current 3D NN-based fluid models.

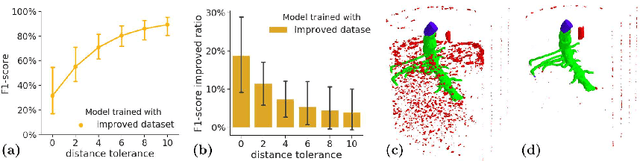
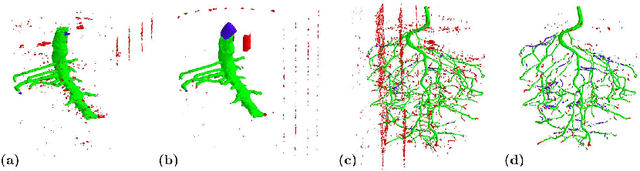
Robust Skeletonization for Plant Root Structure Reconstruction from MRI

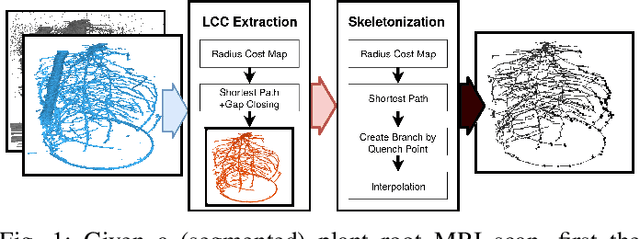
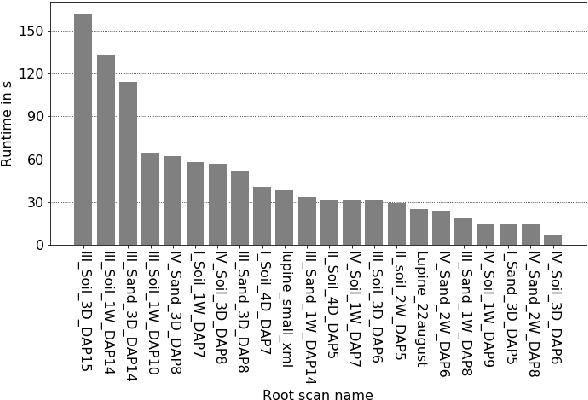
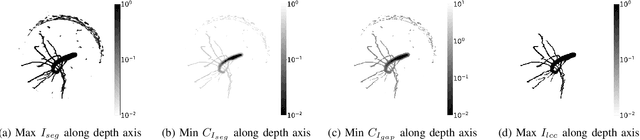
Structural reconstruction of plant roots from MRI is challenging, because of low resolution and low signal-to-noise ratio of the 3D measurements which may lead to disconnectivities and wrongly connected roots. We propose a two-stage approach for this task. The first stage is based on semantic root vs. soil segmentation and finds lowest-cost paths from any root voxel to the shoot. The second stage takes the largest fully connected component generated in the first stage and uses 3D skeletonization to extract a graph structure. We evaluate our method on 22 MRI scans and compare to human expert reconstructions.

Unsupervised Deep Learning of Incompressible Fluid Dynamics

Fast and stable fluid simulations are an essential prerequisite for applications ranging from computer aided aerodynamic design of automobiles or airplanes to simulations of physical effects in CGI to research in meteorology. Recent differentiable fluid simulations allow gradient based methods to optimize e.g. fluid control systems in an informed manner. Solving the partial differential equations governed by the dynamics of the underlying physical systems, however, is a challenging task and current numerical approximation schemes still come at high computational costs. In this work, we propose an unsupervised framework that allows powerful deep neural networks to learn the dynamics of incompressible fluids end to end on a grid-based representation. For this purpose, we introduce a loss function that penalizes residuals of the incompressible Navier Stokes equations. After training, the framework yields models that are capable of fast and differentiable fluid simulations and can handle various fluid phenomena such as the Magnus effect and K\'arm\'an vortex streets. Besides demonstrating its real-time capability on a GPU, we exploit our approach in a control optimization scenario.

3D U-Net for Segmentation of Plant Root MRI Images in Super-Resolution

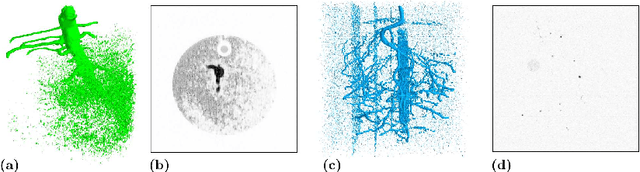
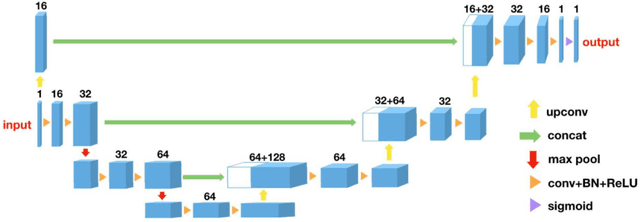
Magnetic resonance imaging (MRI) enables plant scientists to non-invasively study root system development and root-soil interaction. Challenging recording conditions, such as low resolution and a high level of noise hamper the performance of traditional root extraction algorithms, though. We propose to increase signal-to-noise ratio and resolution by segmenting the scanned volumes into root and soil in super-resolution using a 3D U-Net. Tests on real data show that the trained network is capable to detect most roots successfully and even finds roots that were missed by human annotators. Our experiments show that the segmentation performance can be further improved with modifications of the loss function.

Complex Valued Gated Auto-encoder for Video Frame Prediction

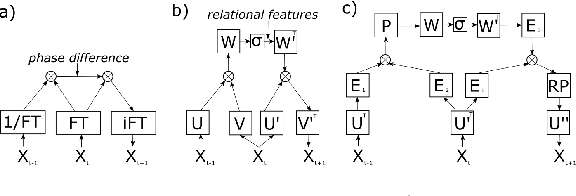
In recent years, complex valued artificial neural networks have gained increasing interest as they allow neural networks to learn richer representations while potentially incorporating less parameters. Especially in the domain of computer graphics, many traditional operations rely heavily on computations in the complex domain, thus complex valued neural networks apply naturally. In this paper, we perform frame predictions in video sequences using a complex valued gated auto-encoder. First, our method is motivated showing how the Fourier transform can be seen as the basis for translational operations. Then, we present how a complex neural network can learn such transformations and compare its performance and parameter efficiency to a real-valued gated autoencoder. Furthermore, we show how extending both - the real and the complex valued - neural networks by using convolutional units can significantly improve prediction performance and parameter efficiency. The networks are assessed on a moving noise and a bouncing ball dataset.