Enhanced Expressivity in Graph Neural Networks with Lanczos-Based Linear Constraints

Graph Neural Networks (GNNs) excel in handling graph-structured data but often underperform in link prediction tasks compared to classical methods, mainly due to the limitations of the commonly used Message Passing GNNs (MPNNs). Notably, their ability to distinguish non-isomorphic graphs is limited by the 1-dimensional Weisfeiler-Lehman test. Our study presents a novel method to enhance the expressivity of GNNs by embedding induced subgraphs into the graph Laplacian matrix's eigenbasis. We introduce a Learnable Lanczos algorithm with Linear Constraints (LLwLC), proposing two novel subgraph extraction strategies: encoding vertex-deleted subgraphs and applying Neumann eigenvalue constraints. For the former, we conjecture that LLwLC establishes a universal approximator, offering efficient time complexity. The latter focuses on link representations enabling differentiation between $k$-regular graphs and node automorphism, a vital aspect for link prediction tasks. Our approach results in an extremely lightweight architecture, reducing the need for extensive training datasets. Empirically, our method improves performance in challenging link prediction tasks across benchmark datasets, establishing its practical utility and supporting our theoretical findings. Notably, LLwLC achieves 20x and 10x speedup by only requiring 5% and 10% data from the PubMed and OGBL-Vessel datasets while comparing to the state-of-the-art.

Occlusion Handling in 3D Human Pose Estimation with Perturbed Positional Encoding

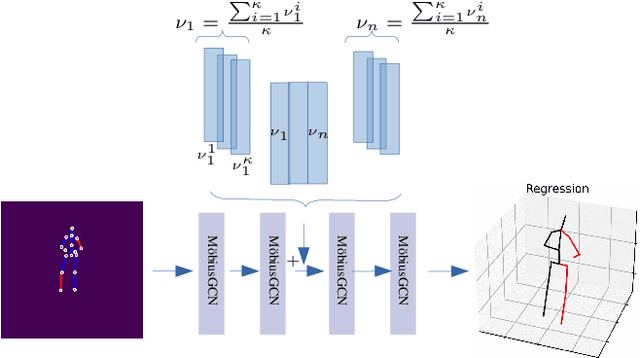
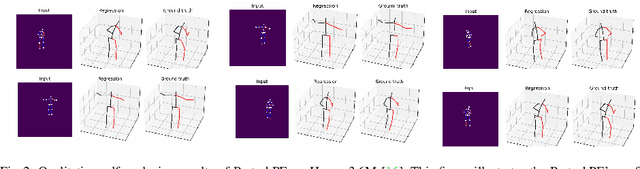
Understanding human behavior fundamentally relies on accurate 3D human pose estimation. Graph Convolutional Networks (GCNs) have recently shown promising advancements, delivering state-of-the-art performance with rather lightweight architectures. In the context of graph-structured data, leveraging the eigenvectors of the graph Laplacian matrix for positional encoding is effective. Yet, the approach does not specify how to handle scenarios where edges in the input graph are missing. To this end, we propose a novel positional encoding technique, PerturbPE, that extracts consistent and regular components from the eigenbasis. Our method involves applying multiple perturbations and taking their average to extract the consistent and regular component from the eigenbasis. PerturbPE leverages the Rayleigh-Schrodinger Perturbation Theorem (RSPT) for calculating the perturbed eigenvectors. Employing this labeling technique enhances the robustness and generalizability of the model. Our results support our theoretical findings, e.g. our experimental analysis observed a performance enhancement of up to $12\%$ on the Human3.6M dataset in instances where occlusion resulted in the absence of one edge. Furthermore, our novel approach significantly enhances performance in scenarios where two edges are missing, setting a new benchmark for state-of-the-art.

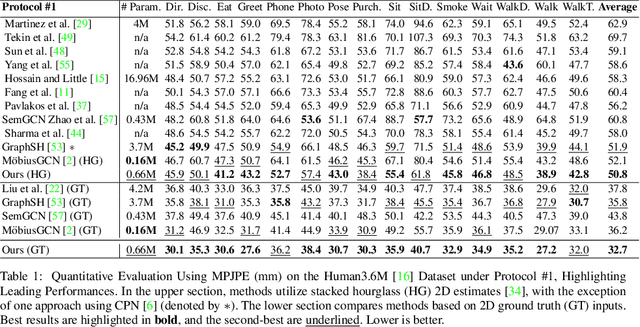
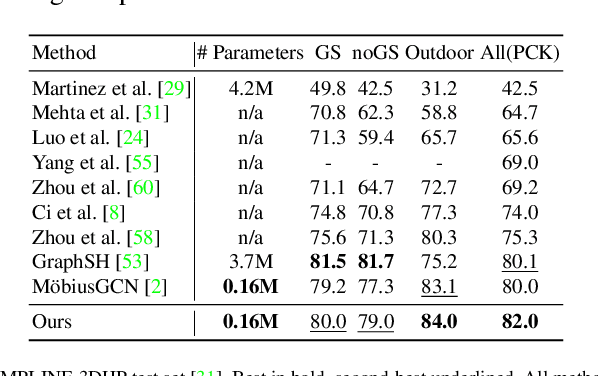
3D Human Pose Estimation Using Möbius Graph Convolutional Networks

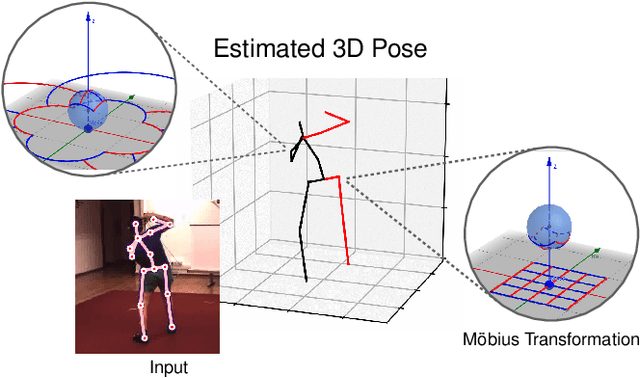
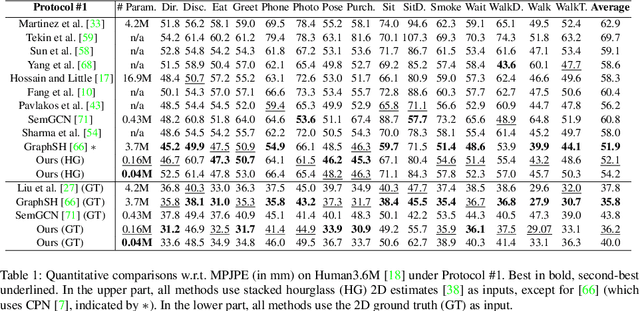
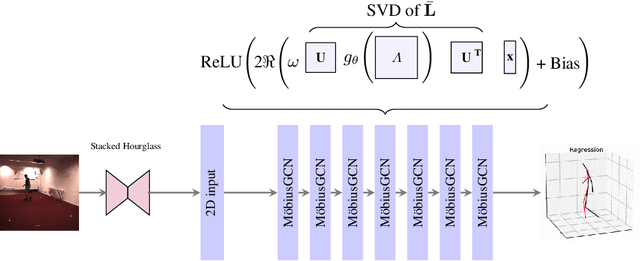
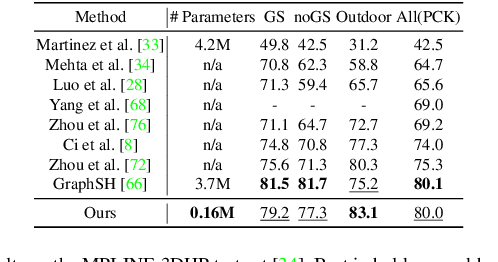
3D human pose estimation is fundamental to understanding human behavior. Recently, promising results have been achieved by graph convolutional networks (GCNs), which achieve state-of-the-art performance and provide rather light-weight architectures. However, a major limitation of GCNs is their inability to encode all the transformations between joints explicitly. To address this issue, we propose a novel spectral GCN using the M\"obius transformation (M\"obiusGCN). In particular, this allows us to directly and explicitly encode the transformation between joints, resulting in a significantly more compact representation. Compared to even the lightest architectures so far, our novel approach requires 90-98% fewer parameters, i.e. our lightest M\"obiusGCN uses only 0.042M trainable parameters. Besides the drastic parameter reduction, explicitly encoding the transformation of joints also enables us to achieve state-of-the-art results. We evaluate our approach on the two challenging pose estimation benchmarks, Human3.6M and MPI-INF-3DHP, demonstrating both state-of-the-art results and the generalization capabilities of M\"obiusGCN.

Complex Valued Gated Auto-encoder for Video Frame Prediction

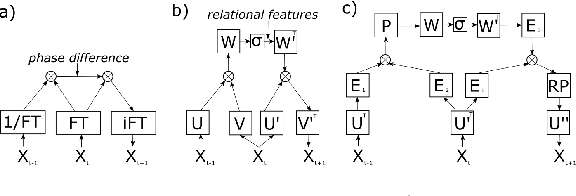
In recent years, complex valued artificial neural networks have gained increasing interest as they allow neural networks to learn richer representations while potentially incorporating less parameters. Especially in the domain of computer graphics, many traditional operations rely heavily on computations in the complex domain, thus complex valued neural networks apply naturally. In this paper, we perform frame predictions in video sequences using a complex valued gated auto-encoder. First, our method is motivated showing how the Fourier transform can be seen as the basis for translational operations. Then, we present how a complex neural network can learn such transformations and compare its performance and parameter efficiency to a real-valued gated autoencoder. Furthermore, we show how extending both - the real and the complex valued - neural networks by using convolutional units can significantly improve prediction performance and parameter efficiency. The networks are assessed on a moving noise and a bouncing ball dataset.

Location Dependency in Video Prediction

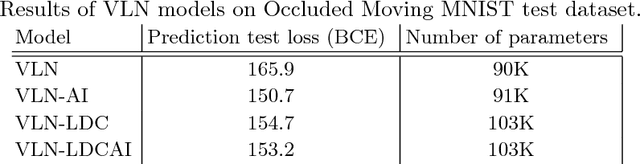
Deep convolutional neural networks are used to address many computer vision problems, including video prediction. The task of video prediction requires analyzing the video frames, temporally and spatially, and constructing a model of how the environment evolves. Convolutional neural networks are spatially invariant, though, which prevents them from modeling location-dependent patterns. In this work, the authors propose location-biased convolutional layers to overcome this limitation. The effectiveness of location bias is evaluated on two architectures: Video Ladder Network (VLN) and Convolutional redictive Gating Pyramid (Conv-PGP). The results indicate that encoding location-dependent features is crucial for the task of video prediction. Our proposed methods significantly outperform spatially invariant models.