Residual Reweighted Conformal Prediction for Graph Neural Networks

Graph Neural Networks (GNNs) excel at modeling relational data but face significant challenges in high-stakes domains due to unquantified uncertainty. Conformal prediction (CP) offers statistical coverage guarantees, but existing methods often produce overly conservative prediction intervals that fail to account for graph heteroscedasticity and structural biases. While residual reweighting CP variants address some of these limitations, they neglect graph topology, cluster-specific uncertainties, and risk data leakage by reusing training sets. To address these issues, we propose Residual Reweighted GNN (RR-GNN), a framework designed to generate minimal prediction sets with provable marginal coverage guarantees. RR-GNN introduces three major innovations to enhance prediction performance. First, it employs Graph-Structured Mondrian CP to partition nodes or edges into communities based on topological features, ensuring cluster-conditional coverage that reflects heterogeneity. Second, it uses Residual-Adaptive Nonconformity Scores by training a secondary GNN on a held-out calibration set to estimate task-specific residuals, dynamically adjusting prediction intervals according to node or edge uncertainty. Third, it adopts a Cross-Training Protocol, which alternates the optimization of the primary GNN and the residual predictor to prevent information leakage while maintaining graph dependencies. We validate RR-GNN on 15 real-world graphs across diverse tasks, including node classification, regression, and edge weight prediction. Compared to CP baselines, RR-GNN achieves improved efficiency over state-of-the-art methods, with no loss of coverage.

Assumption-free fidelity bounds for hardware noise characterization

In the Quantum Supremacy regime, quantum computers may overcome classical machines on several tasks if we can estimate, mitigate, or correct unavoidable hardware noise. Estimating the error requires classical simulations, which become unfeasible in the Quantum Supremacy regime. We leverage Machine Learning data-driven approaches and Conformal Prediction, a Machine Learning uncertainty quantification tool known for its mild assumptions and finite-sample validity, to find theoretically valid upper bounds of the fidelity between noiseless and noisy outputs of quantum devices. Under reasonable extrapolation assumptions, the proposed scheme applies to any Quantum Computing hardware, does not require modeling the device's noise sources, and can be used when classical simulations are unavailable, e.g. in the Quantum Supremacy regime.

Enhanced Route Planning with Calibrated Uncertainty Set

This paper investigates the application of probabilistic prediction methodologies in route planning within a road network context. Specifically, we introduce the Conformalized Quantile Regression for Graph Autoencoders (CQR-GAE), which leverages the conformal prediction technique to offer a coverage guarantee, thus improving the reliability and robustness of our predictions. By incorporating uncertainty sets derived from CQR-GAE, we substantially improve the decision-making process in route planning under a robust optimization framework. We demonstrate the effectiveness of our approach by applying the CQR-GAE model to a real-world traffic scenario. The results indicate that our model significantly outperforms baseline methods, offering a promising avenue for advancing intelligent transportation systems.

State-space models can learn in-context by gradient descent

Deep state-space models (Deep SSMs) have shown capabilities for in-context learning on autoregressive tasks, similar to transformers. However, the architectural requirements and mechanisms enabling this in recurrent networks remain unclear. This study demonstrates that state-space model architectures can perform gradient-based learning and use it for in-context learning. We prove that a single structured state-space model layer, augmented with local self-attention, can reproduce the outputs of an implicit linear model with least squares loss after one step of gradient descent. Our key insight is that the diagonal linear recurrent layer can act as a gradient accumulator, which can be `applied' to the parameters of the implicit regression model. We validate our construction by training randomly initialized augmented SSMs on simple linear regression tasks. The empirically optimized parameters match the theoretical ones, obtained analytically from the implicit model construction. Extensions to multi-step linear and non-linear regression yield consistent results. The constructed SSM encompasses features of modern deep state-space models, with the potential for scalable training and effectiveness even in general tasks. The theoretical construction elucidates the role of local self-attention and multiplicative interactions in recurrent architectures as the key ingredients for enabling the expressive power typical of foundation models.

Entropy Reweighted Conformal Classification

Conformal Prediction (CP) is a powerful framework for constructing prediction sets with guaranteed coverage. However, recent studies have shown that integrating confidence calibration with CP can lead to a degradation in efficiency. In this paper, We propose an adaptive approach that considers the classifier's uncertainty and employs entropy-based reweighting to enhance the efficiency of prediction sets for conformal classification. Our experimental results demonstrate that this method significantly improves efficiency.

Conformal Load Prediction with Transductive Graph Autoencoders

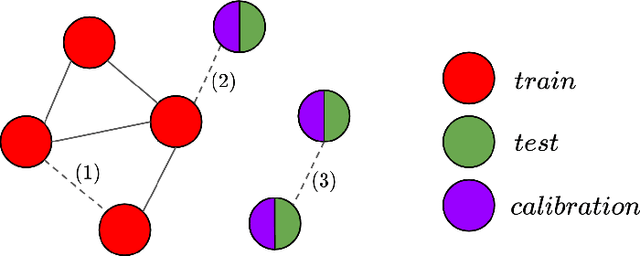
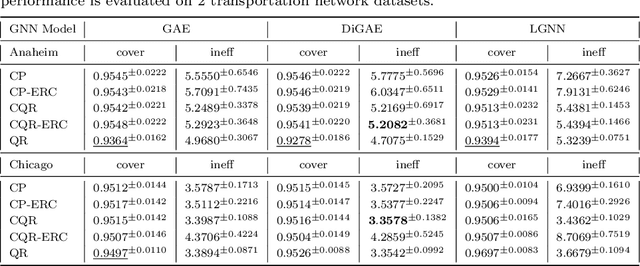
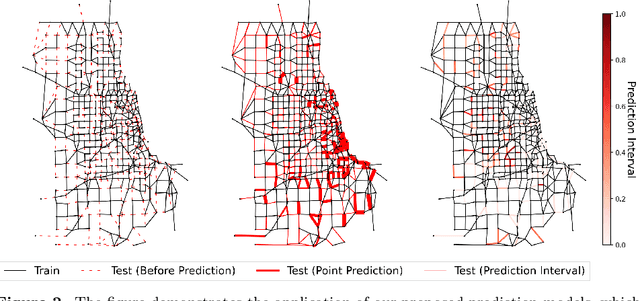
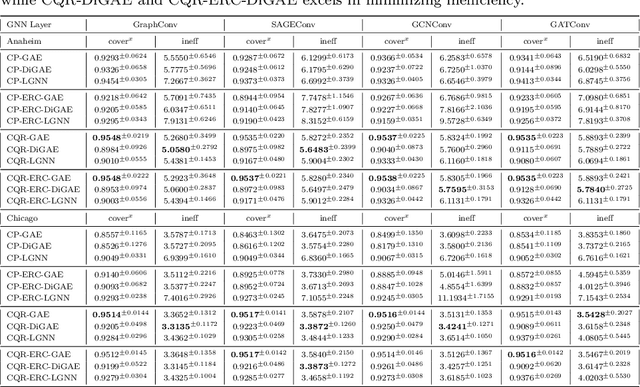
Predicting edge weights on graphs has various applications, from transportation systems to social networks. This paper describes a Graph Neural Network (GNN) approach for edge weight prediction with guaranteed coverage. We leverage conformal prediction to calibrate the GNN outputs and produce valid prediction intervals. We handle data heteroscedasticity through error reweighting and Conformalized Quantile Regression (CQR). We compare the performance of our method against baseline techniques on real-world transportation datasets. Our approach has better coverage and efficiency than all baselines and showcases robustness and adaptability.

Normalizing Flows for Conformal Regression

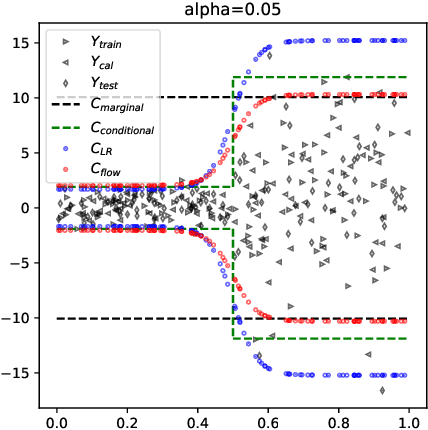
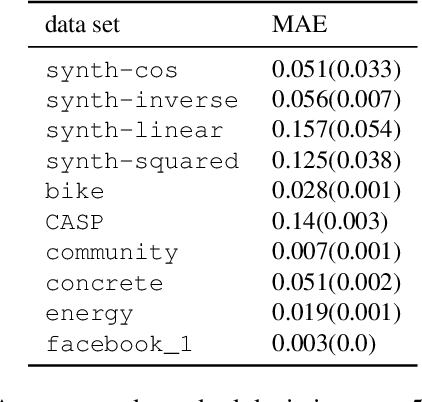
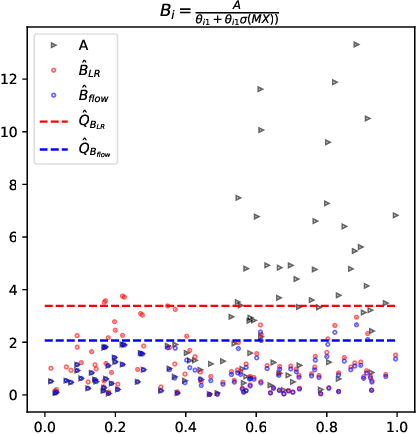
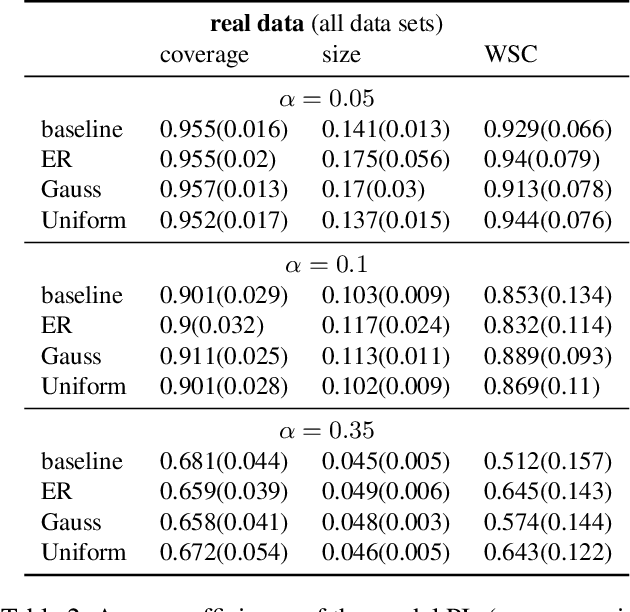
Conformal Prediction (CP) algorithms estimate the uncertainty of a prediction model by calibrating its outputs on labeled data. The same calibration scheme usually applies to any model and data without modifications. The obtained prediction intervals are valid by construction but could be inefficient, i.e. unnecessarily big, if the prediction errors are not uniformly distributed over the input space. We present a general scheme to localize the intervals by training the calibration process. The standard prediction error is replaced by an optimized distance metric that depends explicitly on the object attributes. Learning the optimal metric is equivalent to training a Normalizing Flow that acts on the joint distribution of the errors and the inputs. Unlike the Error Re-weighting CP algorithm of Papadopoulos et al. (2008), the framework allows estimating the gap between nominal and empirical conditional validity. The approach is compatible with existing locally-adaptive CP strategies based on re-weighting the calibration samples and applies to any point-prediction model without retraining.

On training locally adaptive CP

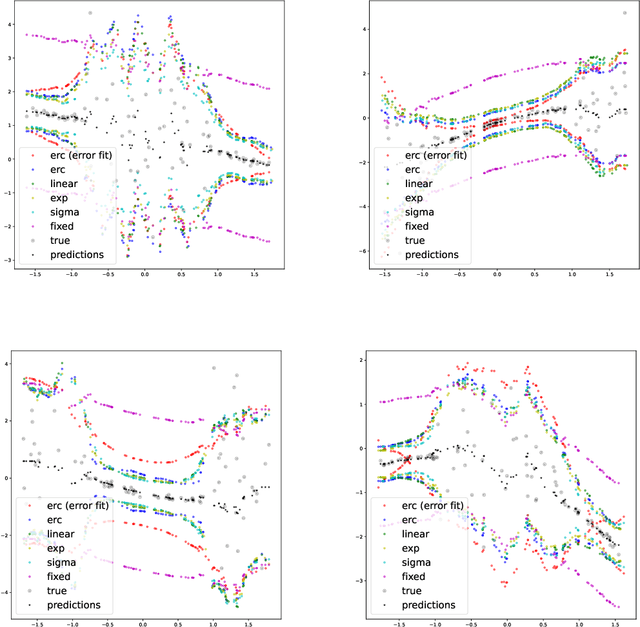
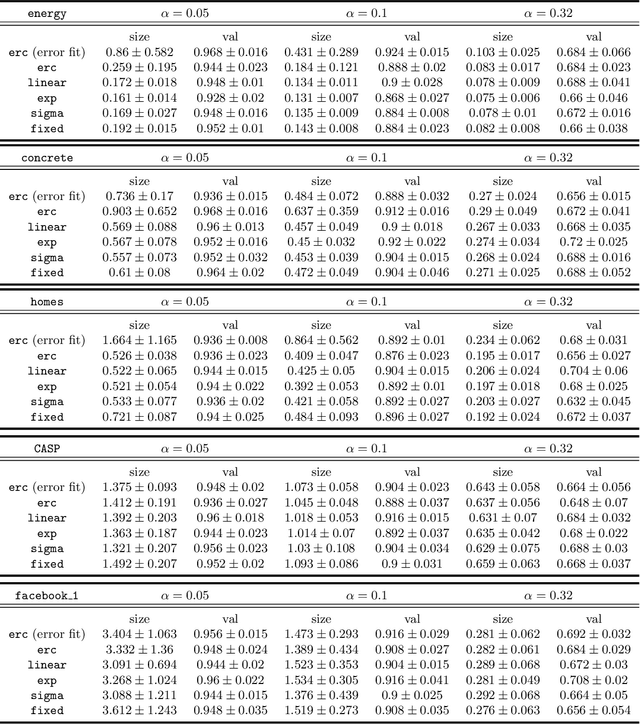
We address the problem of making Conformal Prediction (CP) intervals locally adaptive. Most existing methods focus on approximating the object-conditional validity of the intervals by partitioning or re-weighting the calibration set. Our strategy is new and conceptually different. Instead of re-weighting the calibration data, we redefine the conformity measure through a trainable change of variables, $A \to \phi_X(A)$, that depends explicitly on the object attributes, $X$. Under certain conditions and if $\phi_X$ is monotonic in $A$ for any $X$, the transformations produce prediction intervals that are guaranteed to be marginally valid and have $X$-dependent sizes. We describe how to parameterize and train $\phi_X$ to maximize the interval efficiency. Contrary to other CP-aware training methods, the objective function is smooth and can be minimized through standard gradient methods without approximations.

Differentiable Architecture Pruning for Transfer Learning

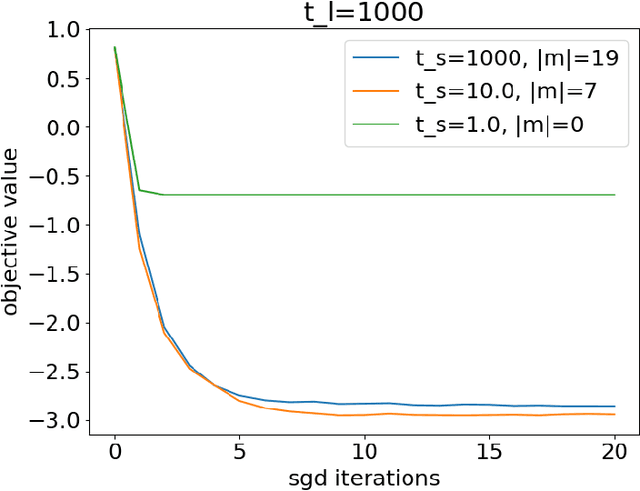
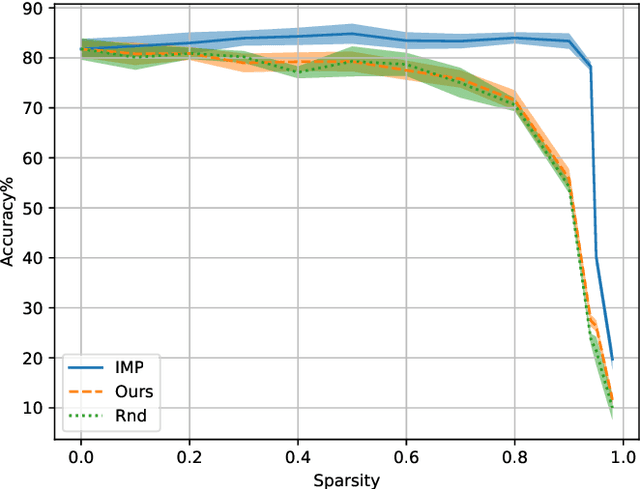
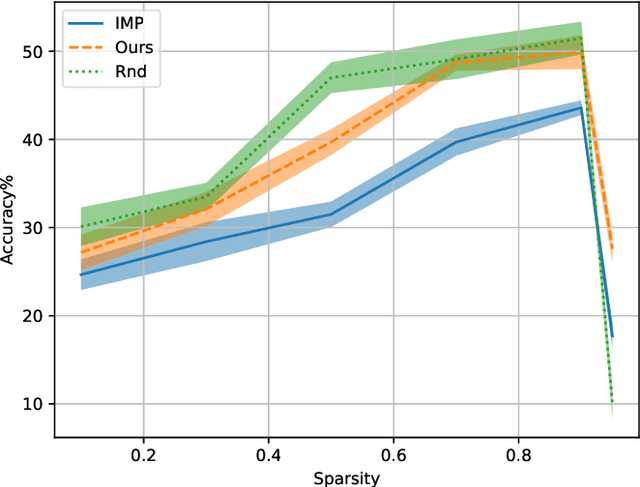
We propose a new gradient-based approach for extracting sub-architectures from a given large model. Contrarily to existing pruning methods, which are unable to disentangle the network architecture and the corresponding weights, our architecture-pruning scheme produces transferable new structures that can be successfully retrained to solve different tasks. We focus on a transfer-learning setup where architectures can be trained on a large data set but very few data points are available for fine-tuning them on new tasks. We define a new gradient-based algorithm that trains architectures of arbitrarily low complexity independently from the attached weights. Given a search space defined by an existing large neural model, we reformulate the architecture search task as a complexity-penalized subset-selection problem and solve it through a two-temperature relaxation scheme. We provide theoretical convergence guarantees and validate the proposed transfer-learning strategy on real data.

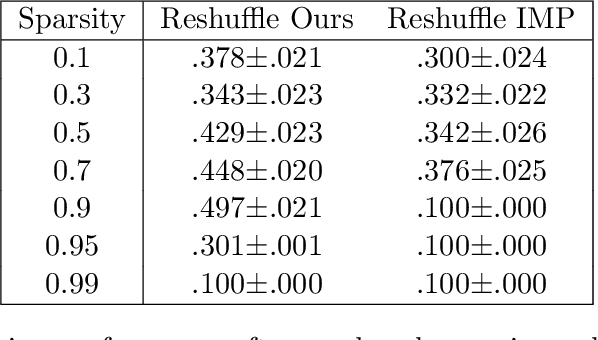
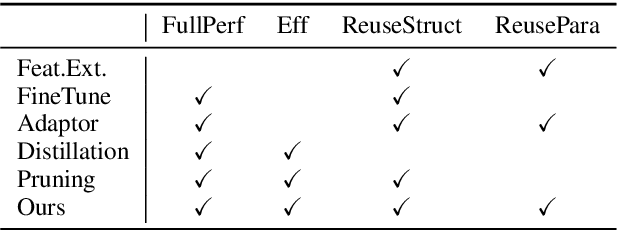
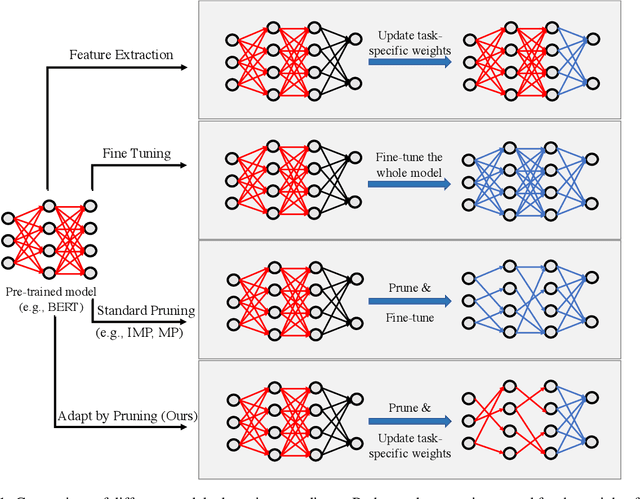
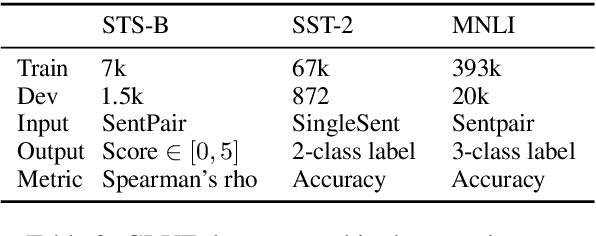
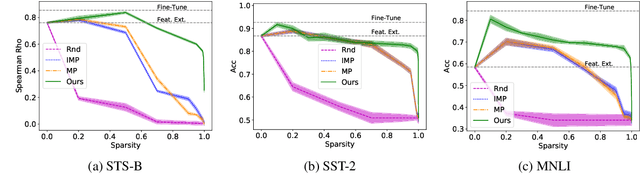
Adapting by Pruning: A Case Study on BERT

Adapting pre-trained neural models to downstream tasks has become the standard practice for obtaining high-quality models. In this work, we propose a novel model adaptation paradigm, adapting by pruning, which prunes neural connections in the pre-trained model to optimise the performance on the target task; all remaining connections have their weights intact. We formulate adapting-by-pruning as an optimisation problem with a differentiable loss and propose an efficient algorithm to prune the model. We prove that the algorithm is near-optimal under standard assumptions and apply the algorithm to adapt BERT to some GLUE tasks. Results suggest that our method can prune up to 50% weights in BERT while yielding similar performance compared to the fine-tuned full model. We also compare our method with other state-of-the-art pruning methods and study the topological differences of their obtained sub-networks.