On training locally adaptive CP
Paper and Code
Jun 05, 2023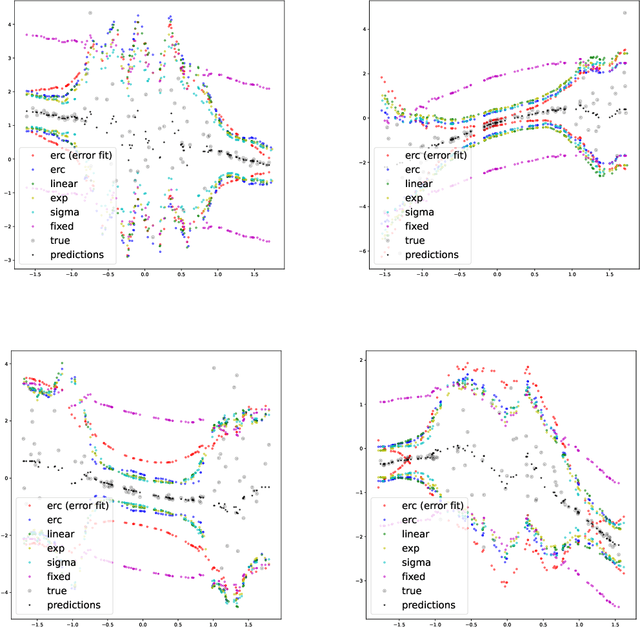
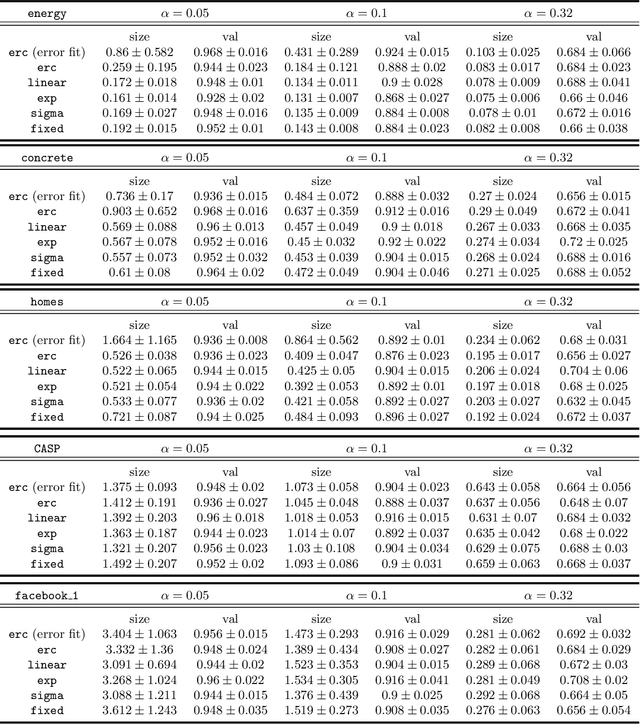
We address the problem of making Conformal Prediction (CP) intervals locally adaptive. Most existing methods focus on approximating the object-conditional validity of the intervals by partitioning or re-weighting the calibration set. Our strategy is new and conceptually different. Instead of re-weighting the calibration data, we redefine the conformity measure through a trainable change of variables, $A \to \phi_X(A)$, that depends explicitly on the object attributes, $X$. Under certain conditions and if $\phi_X$ is monotonic in $A$ for any $X$, the transformations produce prediction intervals that are guaranteed to be marginally valid and have $X$-dependent sizes. We describe how to parameterize and train $\phi_X$ to maximize the interval efficiency. Contrary to other CP-aware training methods, the objective function is smooth and can be minimized through standard gradient methods without approximations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge