Deep Semi-Supervised Anomaly Detection

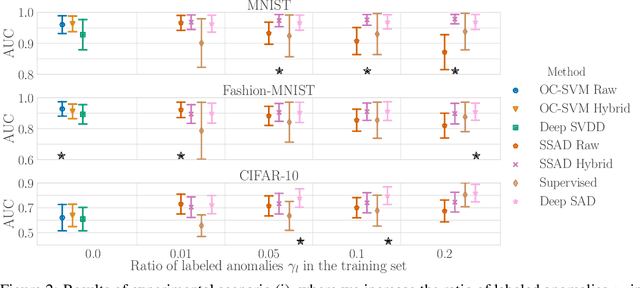
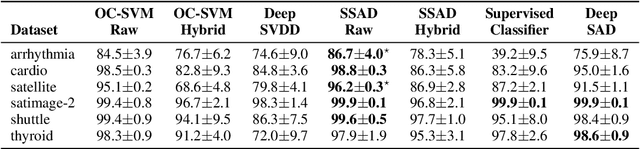
Deep approaches to anomaly detection have recently shown promising results over shallow approaches on high-dimensional data. Typically anomaly detection is treated as an unsupervised learning problem. In practice however, one may have---in addition to a large set of unlabeled samples---access to a small pool of labeled samples, e.g. a subset verified by some domain expert as being normal or anomalous. Semi-supervised approaches to anomaly detection make use of such labeled data to improve detection performance. Few deep semi-supervised approaches to anomaly detection have been proposed so far and those that exist are domain-specific. In this work, we present Deep SAD, an end-to-end methodology for deep semi-supervised anomaly detection. Using an information-theoretic perspective on anomaly detection, we derive a loss motivated by the idea that the entropy for the latent distribution of normal data should be lower than the entropy of the anomalous distribution. We demonstrate in extensive experiments on MNIST, Fashion-MNIST, and CIFAR-10 along with other anomaly detection benchmark datasets that our approach is on par or outperforms shallow, hybrid, and deep competitors, even when provided with only few labeled training data.

Unsupervised Detection and Explanation of Latent-class Contextual Anomalies

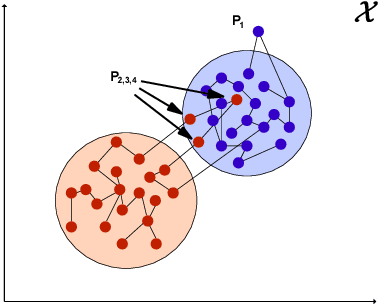
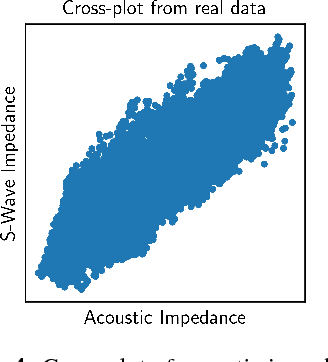
Detecting and explaining anomalies is a challenging effort. This holds especially true when data exhibits strong dependencies and single measurements need to be assessed and analyzed in their respective context. In this work, we consider scenarios where measurements are non-i.i.d, i.e. where samples are dependent on corresponding discrete latent variables which are connected through some given dependency structure, the contextual information. Our contribution is twofold: (i) Building atop of support vector data description (SVDD), we derive a method able to cope with latent-class dependency structure that can still be optimized efficiently. We further show that our approach neatly generalizes vanilla SVDD as well as k-means and conditional random fields (CRF) and provide a corresponding probabilistic interpretation. (ii) In unsupervised scenarios where it is not possible to quantify the accuracy of an anomaly detector, having an human-interpretable solution is the key to success. Based on deep Taylor decomposition and a reformulation of our trained anomaly detector as a neural network, we are able to backpropagate predictions to pixel-domain and thus identify features and regions of high relevance. We demonstrate the usefulness of our novel approach on toy data with known spatio-temporal structure and successfully validate on synthetic as well as real world off-shore data from the oil industry.

Optimizing for Measure of Performance in Max-Margin Parsing

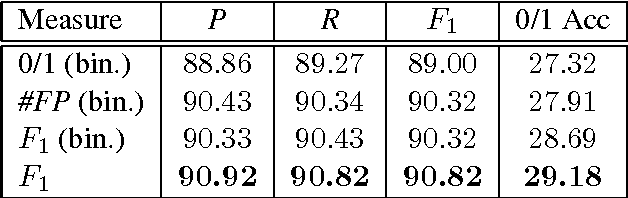
Many statistical learning problems in the area of natural language processing including sequence tagging, sequence segmentation and syntactic parsing has been successfully approached by means of structured prediction methods. An appealing property of the corresponding discriminative learning algorithms is their ability to integrate the loss function of interest directly into the optimization process, which potentially can increase the resulting performance accuracy. Here, we demonstrate on the example of constituency parsing how to optimize for F1-score in the max-margin framework of structural SVM. In particular, the optimization is with respect to the original (not binarized) trees.

Feature Importance Measure for Non-linear Learning Algorithms

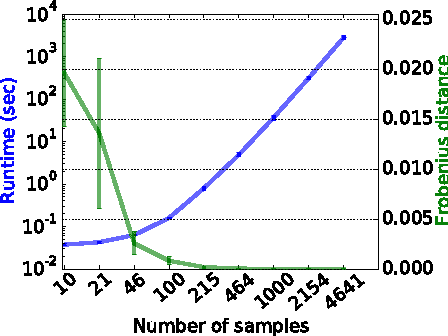
Complex problems may require sophisticated, non-linear learning methods such as kernel machines or deep neural networks to achieve state of the art prediction accuracies. However, high prediction accuracies are not the only objective to consider when solving problems using machine learning. Instead, particular scientific applications require some explanation of the learned prediction function. Unfortunately, most methods do not come with out of the box straight forward interpretation. Even linear prediction functions are not straight forward to explain if features exhibit complex correlation structure. In this paper, we propose the Measure of Feature Importance (MFI). MFI is general and can be applied to any arbitrary learning machine (including kernel machines and deep learning). MFI is intrinsically non-linear and can detect features that by itself are inconspicuous and only impact the prediction function through their interaction with other features. Lastly, MFI can be used for both --- model-based feature importance and instance-based feature importance (i.e, measuring the importance of a feature for a particular data point).