Inexpensive Optical Projection Tomography on a Mobile Phone Platform

This work presents an inexpensive optical projection tomography (OPT) system built on a mobile phone platform for three-dimensional optical microscopy. The system uses an iPhone camera together with a low-cost commercial microscope lens attachment, a stepper motor for sample rotation, LED illumination, and custom 3D-printed components, with a total component cost of approximately 50 US dollars excluding the phone. To support system evaluation, we also developed a low-cost method for fabricating a zebrafish phantom by embedding fixed larvae in UV-cured resin. Camera calibration was performed using a checkerboard target, and effective magnification was estimated with images of a 1951 Air Force resolution target. Projection images acquired during sample rotation were converted to attenuation images and corrected for field nonuniformity. Each slice was reconstructed with filtered backprojection and the resulting slices were stacked into a 3D volume. The completed system achieved a resolution of 3.91 $μm$ and produced volumetric reconstructions in which anatomical features of the zebrafish phantom, including the spine, were clearly visible. These results demonstrate that mobile-phone-based OPT can provide accessible, portable, and low-cost 3D microscopy, with potential utility for education, field work, and resource-limited settings.

SPIRiT Regularization: Parallel MRI with a Combination of Sensitivity Encoding and Linear Predictability

Accelerated Magnetic Resonance Imaging (MRI) permits high quality images from fewer samples that can be collected with a faster scan. Two established methods for accelerating MRI include parallel imaging and compressed sensing. Two types of parallel imaging include linear predictability, which assumes that the Fourier samples are linearly related, and sensitivity encoding, which incorporates a priori knowledge of the sensitivity maps. In this work, we combine compressed sensing with both types of parallel imaging using a novel regularization term: SPIRiT regularization. When combined, the reconstructed images are improved. We demonstrate results on data of a brain, a knee, and an ankle.

Reducing the Sampling Burden of Fourier Sensing with a Non-rectangular Field-of-View

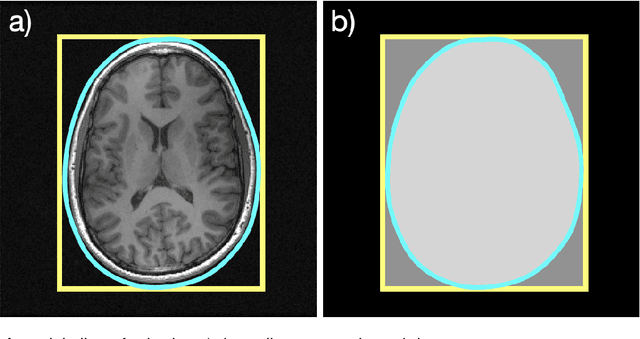
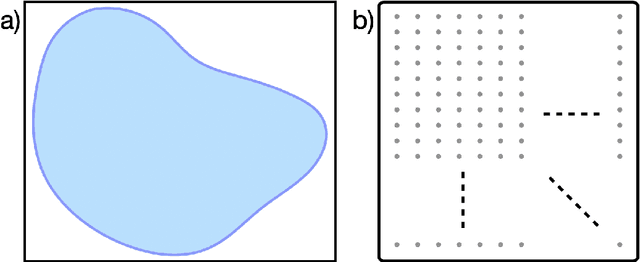
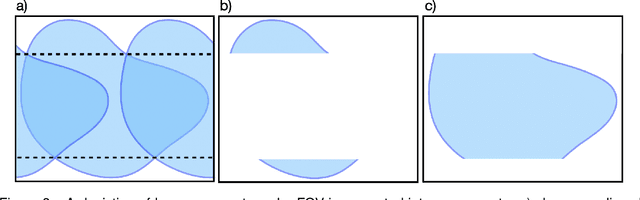
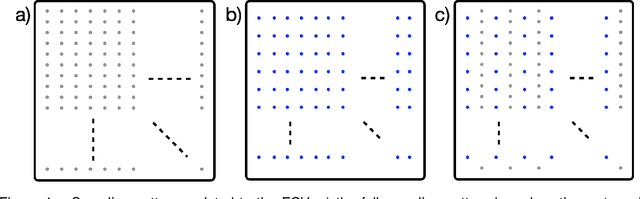
With Fourier sensing, it is commonly the case that the field-of-view (FOV), the area of space to be imaged, is known prior to reconstruction. To date, reconstruction algorithms have focused on FOVs with simple geometries: a rectangle or a hexagon. This yields sampling patterns that are more burdensome than necessary. Due to the reduced area of imaging possible with an arbitrary (e.g., non-rectangular) FOV, the number of samples required for a high-quality images is reduced. However, when an arbitrary FOV has been considered, the reconstruction algorithm is computationally expensive. In this manuscript, we present a method to reduce the sampling pattern for an arbitrary FOV with an accompanying direct (non-iterative) reconstruction algorithm. We also present a method to decrease the computational cost of the (iterative) model-based reconstruction (MBR) algorithm. We present results using MRI data of an ankle, a pineapple, and a brain.

Accelerated Parallel Magnetic Resonance Imaging with Compressed Sensing using Structured Sparsity

Compressed sensing is an imaging paradigm that allows one to invert an underdetermined linear system by imposing the a priori knowledge that the sought after solution is sparse (i.e., mostly zeros). Previous works have shown that if one also knows something about the sparsity pattern (the locations where non-zero entries exist), one can take advantage of this structure to improve the quality of the result. A significant application of compressed sensing is magnetic resonance imaging (MRI), where samples are acquired in the Fourier domain. Compressed sensing allows one to reconstruct a high-quality image with fewer samples which can be collected with a faster scan. This increases the robustness of MRI to patient motion since less motion is possible during the shorter scan. Parallel imaging, where multiple coils are used to gather data, is another an more ubiquitously used method for accelerating MRI. Existing combinations of these acceleration methods, such as Sparse SENSE, yield high quality images with an even shorter scan time than either technique alone. In this work, we show how to modify Sparse SENSE with structured sparsity to reconstruct a high quality image with even fewer samples.

The Dependence of Parallel Imaging with Linear Predictability on the Undersampling Direction

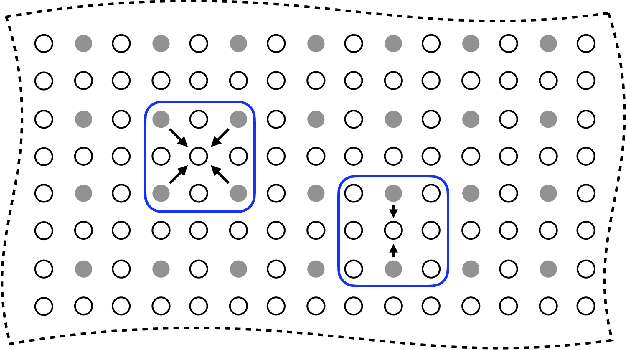
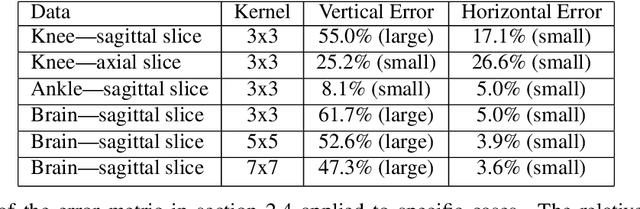
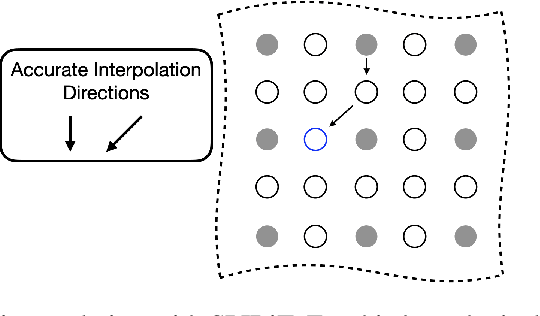
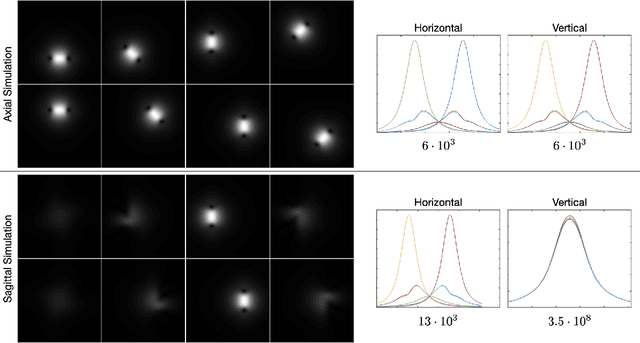
Parallel imaging with linear predictability takes advantage of information present in multiple receive coils to accurately reconstruct the image with fewer samples. Commonly used algorithms based on linear predictability include GRAPPA and SPIRiT. We present a sufficient condition for reconstruction based on the direction of undersampling and the arrangement of the sensing coils. This condition is justified theoretically and examples are shown using real data. We also propose a metric based on the fully-sampled auto-calibration region which can show which direction(s) of undersampling will allow for a good quality image reconstruction.

Physics-driven Deep Learning for PET/MRI

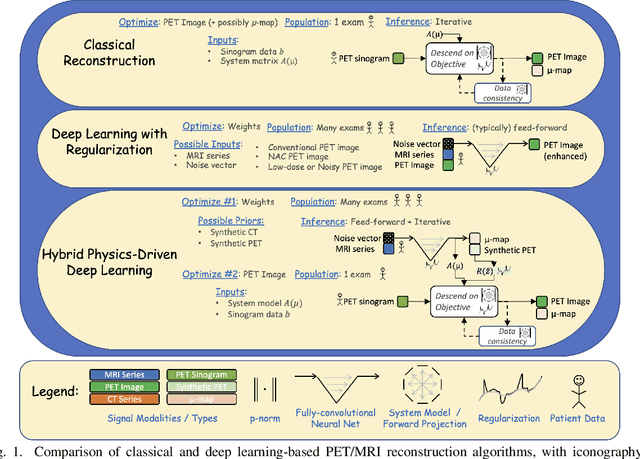
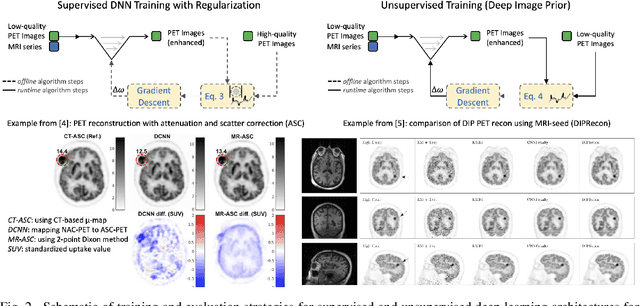
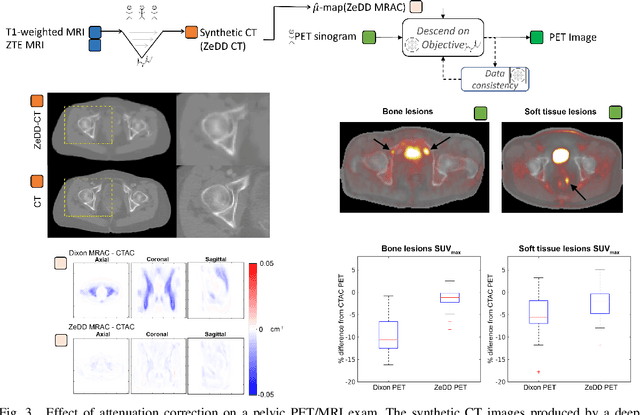
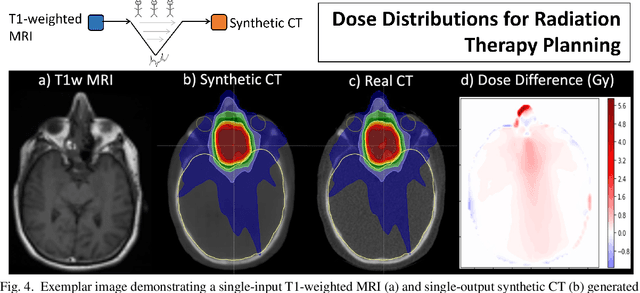
In this paper, we review physics- and data-driven reconstruction techniques for simultaneous positron emission tomography (PET) / magnetic resonance imaging (MRI) systems, which have significant advantages for clinical imaging of cancer, neurological disorders, and heart disease. These reconstruction approaches utilize priors, either structural or statistical, together with a physics-based description of the PET system response. However, due to the nested representation of the forward problem, direct PET/MRI reconstruction is a nonlinear problem. We elucidate how a multi-faceted approach accommodates hybrid data- and physics-driven machine learning for reconstruction of 3D PET/MRI, summarizing important deep learning developments made in the last 5 years to address attenuation correction, scattering, low photon counts, and data consistency. We also describe how applications of these multi-modality approaches extend beyond PET/MRI to improving accuracy in radiation therapy planning. We conclude by discussing opportunities for extending the current state-of-the-art following the latest trends in physics- and deep learning-based computational imaging and next-generation detector hardware.

Least Squares Optimal Density Compensation for the Gridding Non-uniform Discrete Fourier Transform

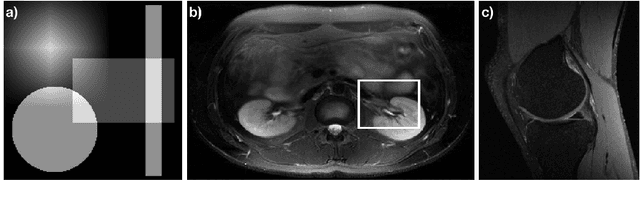
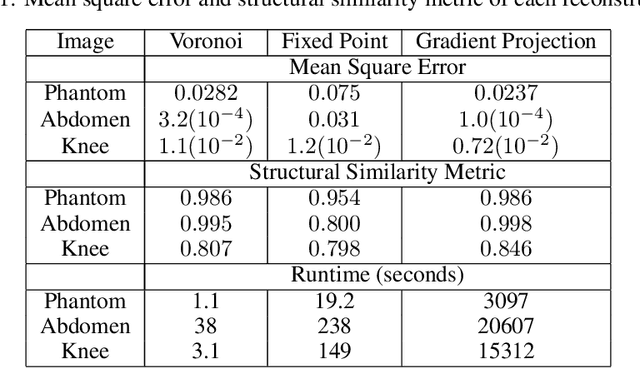
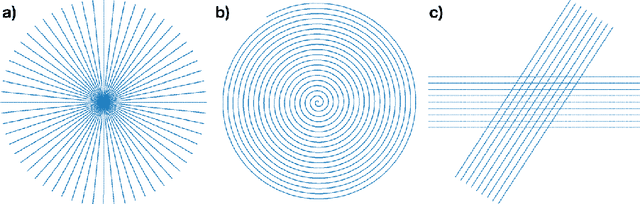
The Gridding algorithm has shown great utility for reconstructing images from non-uniformly spaced samples in the Fourier domain in several imaging modalities. Due to the non-uniform spacing, some correction for the variable density of the samples must be made. Existing methods for generating density compensation values are either sub-optimal or only consider a finite set of points (a set of measure 0) in the optimization. This manuscript presents the first density compensation algorithm for a general trajectory that takes into account the point spread function over a set of non-zero measure. We show that the images reconstructed with Gridding using the density compensation values of this method are of superior quality when compared to density compensation weights determined in other ways. Results are shown with a numerical phantom and with magnetic resonance images of the abdomen and the knee.