Least Squares Optimal Density Compensation for the Gridding Non-uniform Discrete Fourier Transform

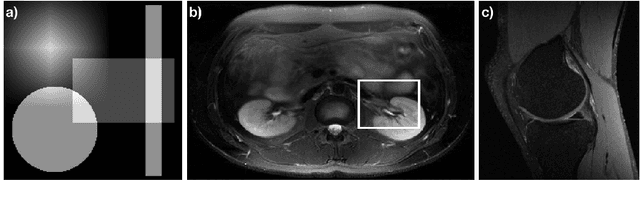
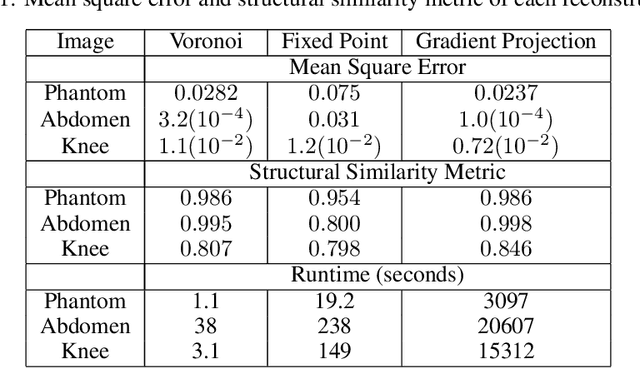
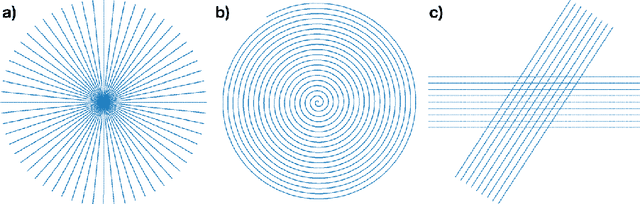
The Gridding algorithm has shown great utility for reconstructing images from non-uniformly spaced samples in the Fourier domain in several imaging modalities. Due to the non-uniform spacing, some correction for the variable density of the samples must be made. Existing methods for generating density compensation values are either sub-optimal or only consider a finite set of points (a set of measure 0) in the optimization. This manuscript presents the first density compensation algorithm for a general trajectory that takes into account the point spread function over a set of non-zero measure. We show that the images reconstructed with Gridding using the density compensation values of this method are of superior quality when compared to density compensation weights determined in other ways. Results are shown with a numerical phantom and with magnetic resonance images of the abdomen and the knee.

Reconstruction of Undersampled 3D Non-Cartesian Image-Based Navigators for Coronary MRA Using an Unrolled Deep Learning Model

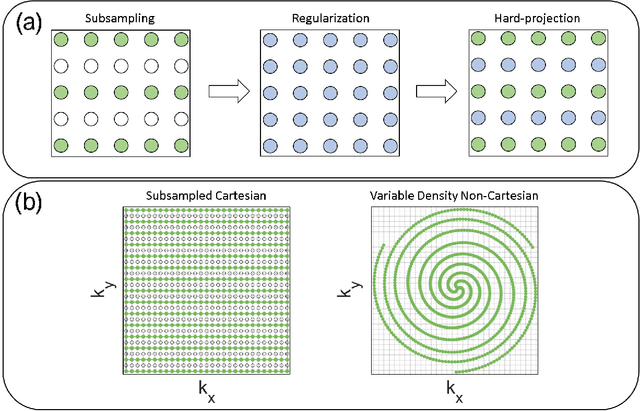
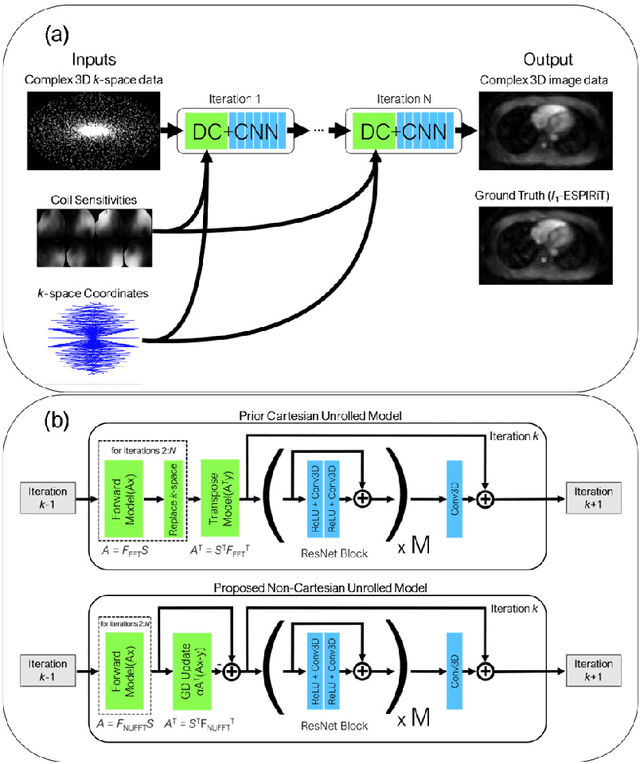
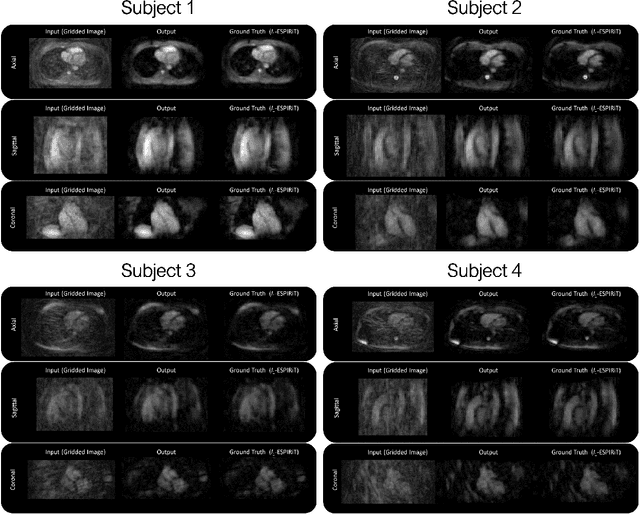
Purpose: To rapidly reconstruct undersampled 3D non-Cartesian image-based navigators (iNAVs) using an unrolled deep learning (DL) model for non-rigid motion correction in coronary magnetic resonance angiography (CMRA). Methods: An unrolled network is trained to reconstruct beat-to-beat 3D iNAVs acquired as part of a CMRA sequence. The unrolled model incorporates a non-uniform FFT operator to perform the data consistency operation, and the regularization term is learned by a convolutional neural network (CNN) based on the proximal gradient descent algorithm. The training set includes 6,000 3D iNAVs acquired from 7 different subjects and 11 scans using a variable-density (VD) cones trajectory. For testing, 3D iNAVs from 4 additional subjects are reconstructed using the unrolled model. To validate reconstruction accuracy, global and localized motion estimates from DL model-based 3D iNAVs are compared with those extracted from 3D iNAVs reconstructed with $\textit{l}_{1}$-ESPIRiT. Then, the high-resolution coronary MRA images motion corrected with autofocusing using the $\textit{l}_{1}$-ESPIRiT and DL model-based 3D iNAVs are assessed for differences. Results: 3D iNAVs reconstructed using the DL model-based approach and conventional $\textit{l}_{1}$-ESPIRiT generate similar global and localized motion estimates and provide equivalent coronary image quality. Reconstruction with the unrolled network completes in a fraction of the time compared to CPU and GPU implementations of $\textit{l}_{1}$-ESPIRiT (20x and 3x speed increases, respectively). Conclusion: We have developed a deep neural network architecture to reconstruct undersampled 3D non-Cartesian VD cones iNAVs. Our approach decreases reconstruction time for 3D iNAVs, while preserving the accuracy of non-rigid motion information offered by them for correction.