Reducing the Sampling Burden of Fourier Sensing with a Non-rectangular Field-of-View

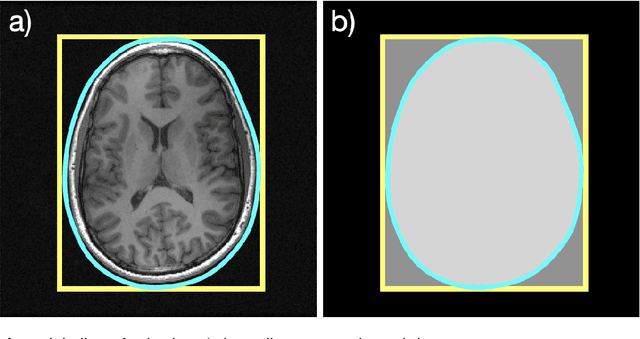
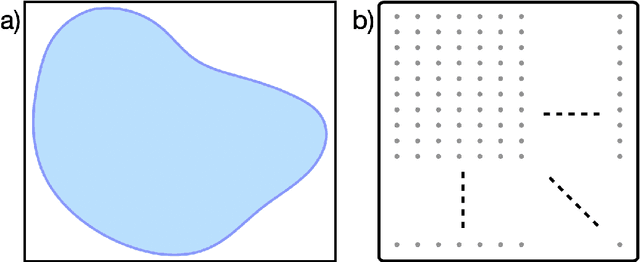
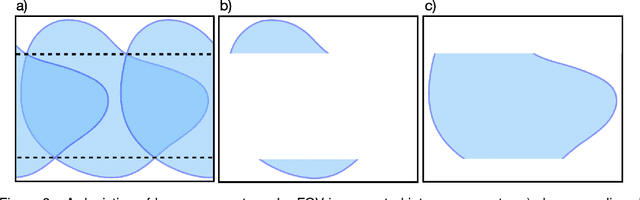
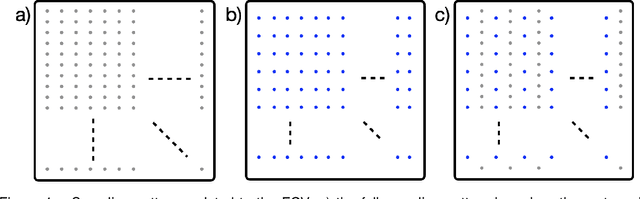
With Fourier sensing, it is commonly the case that the field-of-view (FOV), the area of space to be imaged, is known prior to reconstruction. To date, reconstruction algorithms have focused on FOVs with simple geometries: a rectangle or a hexagon. This yields sampling patterns that are more burdensome than necessary. Due to the reduced area of imaging possible with an arbitrary (e.g., non-rectangular) FOV, the number of samples required for a high-quality images is reduced. However, when an arbitrary FOV has been considered, the reconstruction algorithm is computationally expensive. In this manuscript, we present a method to reduce the sampling pattern for an arbitrary FOV with an accompanying direct (non-iterative) reconstruction algorithm. We also present a method to decrease the computational cost of the (iterative) model-based reconstruction (MBR) algorithm. We present results using MRI data of an ankle, a pineapple, and a brain.

Accelerated Parallel Magnetic Resonance Imaging with Compressed Sensing using Structured Sparsity

Compressed sensing is an imaging paradigm that allows one to invert an underdetermined linear system by imposing the a priori knowledge that the sought after solution is sparse (i.e., mostly zeros). Previous works have shown that if one also knows something about the sparsity pattern (the locations where non-zero entries exist), one can take advantage of this structure to improve the quality of the result. A significant application of compressed sensing is magnetic resonance imaging (MRI), where samples are acquired in the Fourier domain. Compressed sensing allows one to reconstruct a high-quality image with fewer samples which can be collected with a faster scan. This increases the robustness of MRI to patient motion since less motion is possible during the shorter scan. Parallel imaging, where multiple coils are used to gather data, is another an more ubiquitously used method for accelerating MRI. Existing combinations of these acceleration methods, such as Sparse SENSE, yield high quality images with an even shorter scan time than either technique alone. In this work, we show how to modify Sparse SENSE with structured sparsity to reconstruct a high quality image with even fewer samples.