Ground Truth Bias in External Cluster Validity Indices

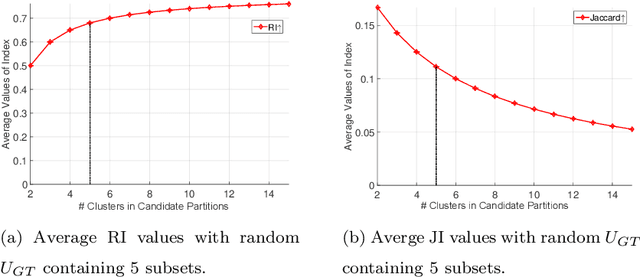
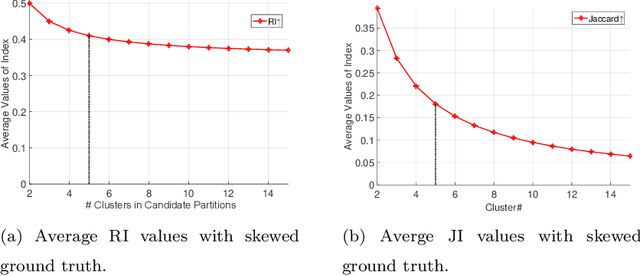
It has been noticed that some external CVIs exhibit a preferential bias towards a larger or smaller number of clusters which is monotonic (directly or inversely) in the number of clusters in candidate partitions. This type of bias is caused by the functional form of the CVI model. For example, the popular Rand index (RI) exhibits a monotone increasing (NCinc) bias, while the Jaccard Index (JI) index suffers from a monotone decreasing (NCdec) bias. This type of bias has been previously recognized in the literature. In this work, we identify a new type of bias arising from the distribution of the ground truth (reference) partition against which candidate partitions are compared. We call this new type of bias ground truth (GT) bias. This type of bias occurs if a change in the reference partition causes a change in the bias status (e.g., NCinc, NCdec) of a CVI. For example, NCinc bias in the RI can be changed to NCdec bias by skewing the distribution of clusters in the ground truth partition. It is important for users to be aware of this new type of biased behaviour, since it may affect the interpretations of CVI results. The objective of this article is to study the empirical and theoretical implications of GT bias. To the best of our knowledge, this is the first extensive study of such a property for external cluster validity indices.

A Framework to Adjust Dependency Measure Estimates for Chance

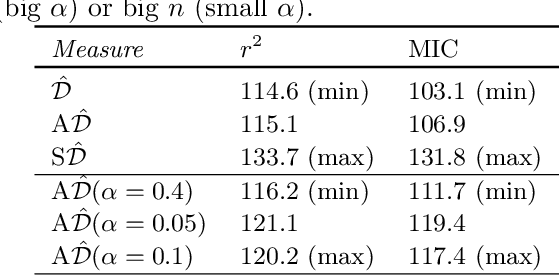
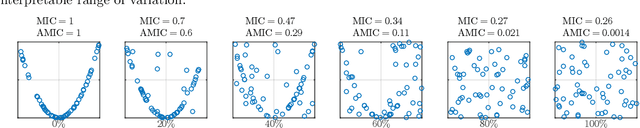
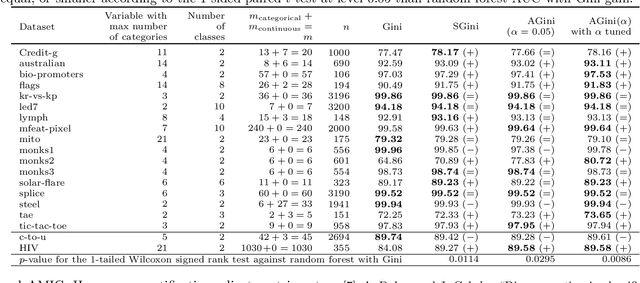
Estimating the strength of dependency between two variables is fundamental for exploratory analysis and many other applications in data mining. For example: non-linear dependencies between two continuous variables can be explored with the Maximal Information Coefficient (MIC); and categorical variables that are dependent to the target class are selected using Gini gain in random forests. Nonetheless, because dependency measures are estimated on finite samples, the interpretability of their quantification and the accuracy when ranking dependencies become challenging. Dependency estimates are not equal to 0 when variables are independent, cannot be compared if computed on different sample size, and they are inflated by chance on variables with more categories. In this paper, we propose a framework to adjust dependency measure estimates on finite samples. Our adjustments, which are simple and applicable to any dependency measure, are helpful in improving interpretability when quantifying dependency and in improving accuracy on the task of ranking dependencies. In particular, we demonstrate that our approach enhances the interpretability of MIC when used as a proxy for the amount of noise between variables, and to gain accuracy when ranking variables during the splitting procedure in random forests.

Adjusting for Chance Clustering Comparison Measures

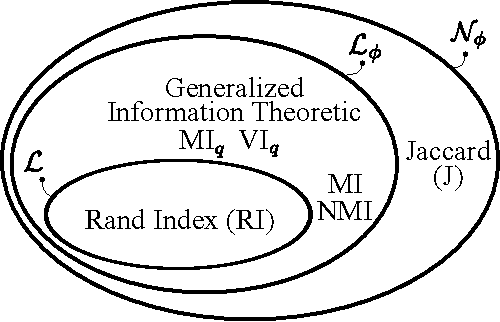
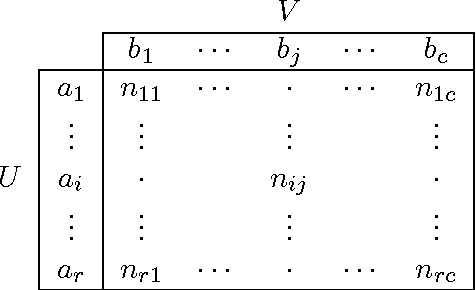
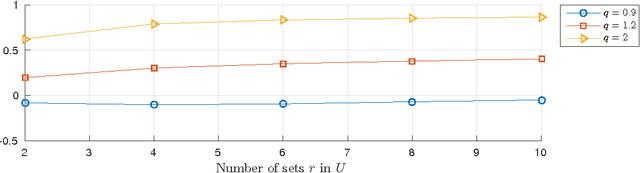
Adjusted for chance measures are widely used to compare partitions/clusterings of the same data set. In particular, the Adjusted Rand Index (ARI) based on pair-counting, and the Adjusted Mutual Information (AMI) based on Shannon information theory are very popular in the clustering community. Nonetheless it is an open problem as to what are the best application scenarios for each measure and guidelines in the literature for their usage are sparse, with the result that users often resort to using both. Generalized Information Theoretic (IT) measures based on the Tsallis entropy have been shown to link pair-counting and Shannon IT measures. In this paper, we aim to bridge the gap between adjustment of measures based on pair-counting and measures based on information theory. We solve the key technical challenge of analytically computing the expected value and variance of generalized IT measures. This allows us to propose adjustments of generalized IT measures, which reduce to well known adjusted clustering comparison measures as special cases. Using the theory of generalized IT measures, we are able to propose the following guidelines for using ARI and AMI as external validation indices: ARI should be used when the reference clustering has large equal sized clusters; AMI should be used when the reference clustering is unbalanced and there exist small clusters.