A Framework to Adjust Dependency Measure Estimates for Chance
Paper and Code
Jan 20, 2016
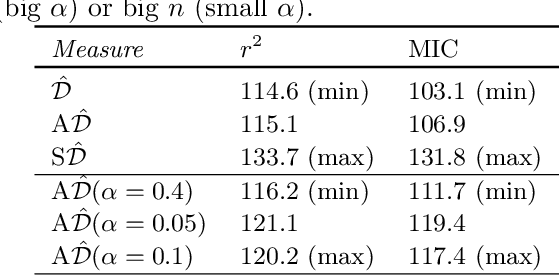
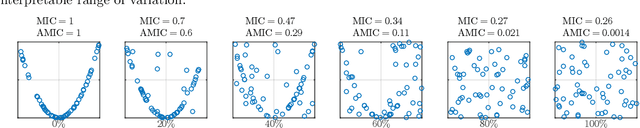
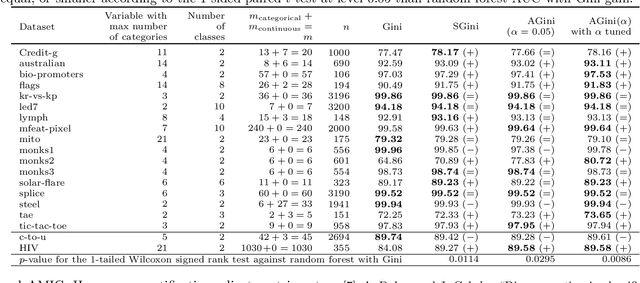
Estimating the strength of dependency between two variables is fundamental for exploratory analysis and many other applications in data mining. For example: non-linear dependencies between two continuous variables can be explored with the Maximal Information Coefficient (MIC); and categorical variables that are dependent to the target class are selected using Gini gain in random forests. Nonetheless, because dependency measures are estimated on finite samples, the interpretability of their quantification and the accuracy when ranking dependencies become challenging. Dependency estimates are not equal to 0 when variables are independent, cannot be compared if computed on different sample size, and they are inflated by chance on variables with more categories. In this paper, we propose a framework to adjust dependency measure estimates on finite samples. Our adjustments, which are simple and applicable to any dependency measure, are helpful in improving interpretability when quantifying dependency and in improving accuracy on the task of ranking dependencies. In particular, we demonstrate that our approach enhances the interpretability of MIC when used as a proxy for the amount of noise between variables, and to gain accuracy when ranking variables during the splitting procedure in random forests.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge