Negash Begashaw
A Multi-Scale Isolation Forest Approach for Real-Time Detection and Filtering of FGSM Adversarial Attacks in Video Streams of Autonomous Vehicles
Feb 22, 2025



Abstract:Deep Neural Networks (DNNs) have demonstrated remarkable success across a wide range of tasks, particularly in fields such as image classification. However, DNNs are highly susceptible to adversarial attacks, where subtle perturbations are introduced to input images, leading to erroneous model outputs. In today's digital era, ensuring the security and integrity of images processed by DNNs is of critical importance. One of the most prominent adversarial attack methods is the Fast Gradient Sign Method (FGSM), which perturbs images in the direction of the loss gradient to deceive the model. This paper presents a novel approach for detecting and filtering FGSM adversarial attacks in image processing tasks. Our proposed method evaluates 10,000 images, each subjected to five different levels of perturbation, characterized by $\epsilon$ values of 0.01, 0.02, 0.05, 0.1, and 0.2. These perturbations are applied in the direction of the loss gradient. We demonstrate that our approach effectively filters adversarially perturbed images, mitigating the impact of FGSM attacks. The method is implemented in Python, and the source code is publicly available on GitHub for reproducibility and further research.
A Robust Adversarial Ensemble with Causal (Feature Interaction) Interpretations for Image Classification
Dec 28, 2024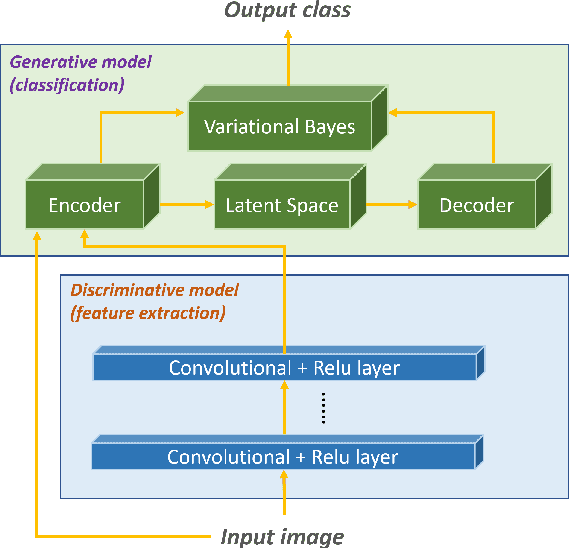
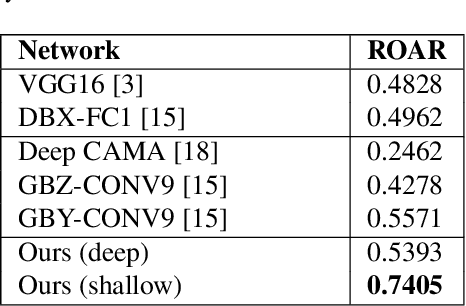
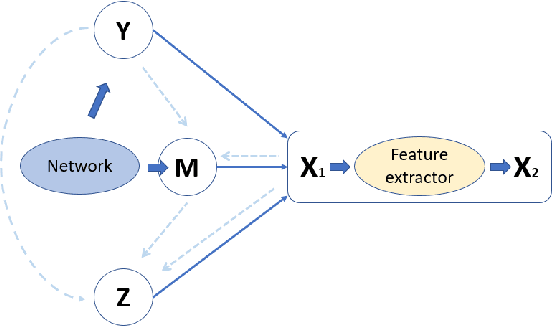
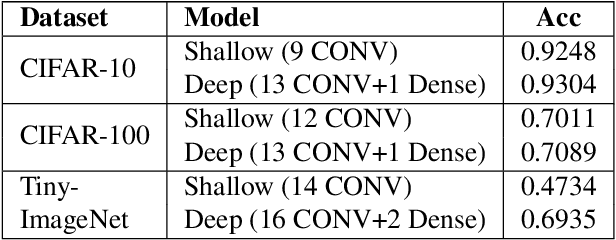
Abstract:Deep learning-based discriminative classifiers, despite their remarkable success, remain vulnerable to adversarial examples that can mislead model predictions. While adversarial training can enhance robustness, it fails to address the intrinsic vulnerability stemming from the opaque nature of these black-box models. We present a deep ensemble model that combines discriminative features with generative models to achieve both high accuracy and adversarial robustness. Our approach integrates a bottom-level pre-trained discriminative network for feature extraction with a top-level generative classification network that models adversarial input distributions through a deep latent variable model. Using variational Bayes, our model achieves superior robustness against white-box adversarial attacks without adversarial training. Extensive experiments on CIFAR-10 and CIFAR-100 demonstrate our model's superior adversarial robustness. Through evaluations using counterfactual metrics and feature interaction-based metrics, we establish correlations between model interpretability and adversarial robustness. Additionally, preliminary results on Tiny-ImageNet validate our approach's scalability to more complex datasets, offering a practical solution for developing robust image classification models.
Boundary-to-Solution Mapping for Groundwater Flows in a Toth Basin
Mar 28, 2023



Abstract:In this paper, the authors propose a new approach to solving the groundwater flow equation in the Toth basin of arbitrary top and bottom topographies using deep learning. Instead of using traditional numerical solvers, they use a DeepONet to produce the boundary-to-solution mapping. This mapping takes the geometry of the physical domain along with the boundary conditions as inputs to output the steady state solution of the groundwater flow equation. To implement the DeepONet, the authors approximate the top and bottom boundaries using truncated Fourier series or piecewise linear representations. They present two different implementations of the DeepONet: one where the Toth basin is embedded in a rectangular computational domain, and another where the Toth basin with arbitrary top and bottom boundaries is mapped into a rectangular computational domain via a nonlinear transformation. They implement the DeepONet with respect to the Dirichlet and Robin boundary condition at the top and the Neumann boundary condition at the impervious bottom boundary, respectively. Using this deep-learning enabled tool, the authors investigate the impact of surface topography on the flow pattern by both the top surface and the bottom impervious boundary with arbitrary geometries. They discover that the average slope of the top surface promotes long-distance transport, while the local curvature controls localized circulations. Additionally, they find that the slope of the bottom impervious boundary can seriously impact the long-distance transport of groundwater flows. Overall, this paper presents a new and innovative approach to solving the groundwater flow equation using deep learning, which allows for the investigation of the impact of surface topography on groundwater flow patterns.
Bayesian Parameter Estimations for Grey System Models in Online Traffic Speed Predictions
Aug 15, 2021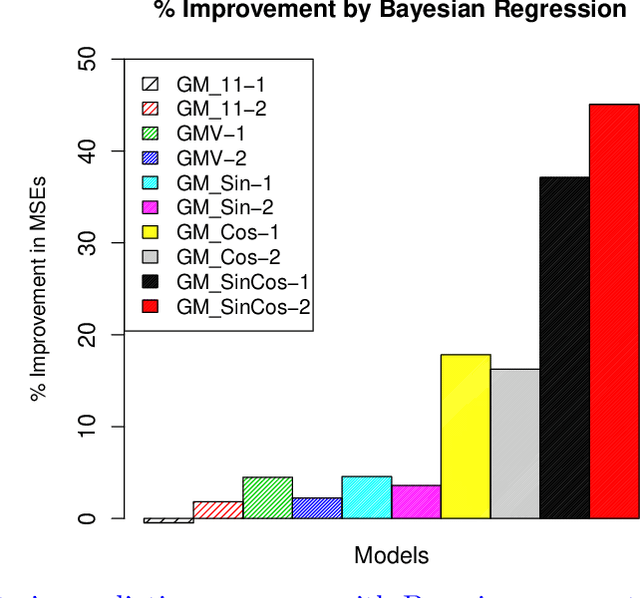
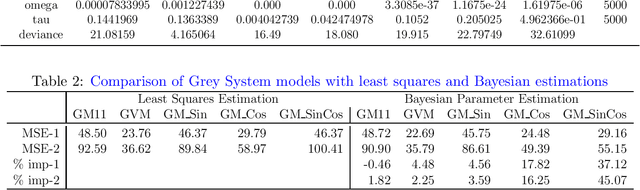
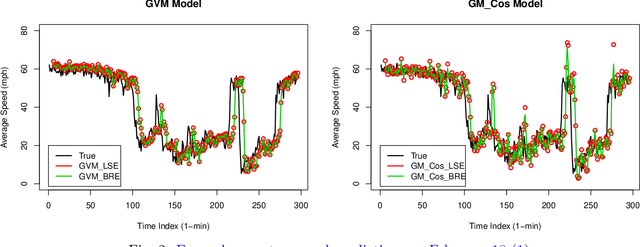
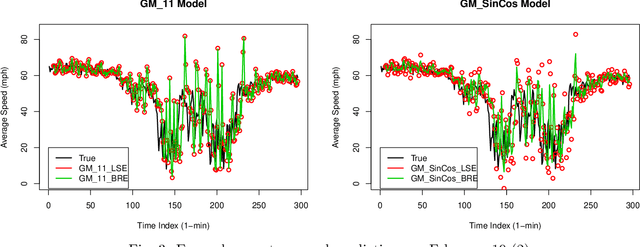
Abstract:This paper presents Bayesian parameter estimation for first order Grey system models' parameters (or sometimes referred to as hyperparameters). There are different forms of first-order Grey System Models. These include $GM(1,1)$, $GM(1,1| \cos(\omega t)$, $GM(1,1| \sin(\omega t)$, and $GM(1,1| \cos(\omega t), \sin(\omega t)$. The whitenization equation of these models is a first-order linear differential equation of the form \[ \frac{dx}{dt} + a x = f(t) \] where $a$ is a parameter and $f(t) = b$ in $GM(1,1|)$ , $f(t) = b_1\cos(\omega t) + b_2$ in $GM(1,1| cos(\omega t)$, $f(t) = b_1\sin(\omega t)+b_2$ in $GM(1,1| \sin(\omega t)$, $f(t) = b_1\sin(\omega t) + b_2\cos(\omega t) + b_3$ in $GM(1,1| \cos(\omega t), \sin(\omega t)$, $f(t) = b x^2$ in Grey Verhulst model (GVM), and where $b, b_1, b_2$, and $b_3$ are parameters. The results from Bayesian estimations are compared to the least square estimated models with fixed $\omega$. We found that using rolling Bayesian estimations for GM parameters can allow us to estimate the parameters in all possible forms. Based on the data used for the comparison, the numerical results showed that models with Bayesian parameter estimations are up to 45\% more accurate in mean squared errors.
Improved Grey System Models for Predicting Traffic Parameters
Nov 18, 2020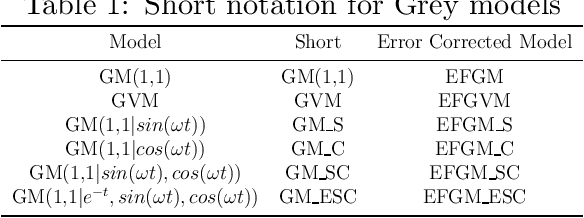
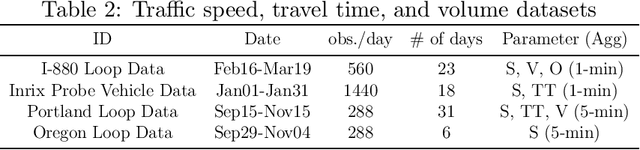
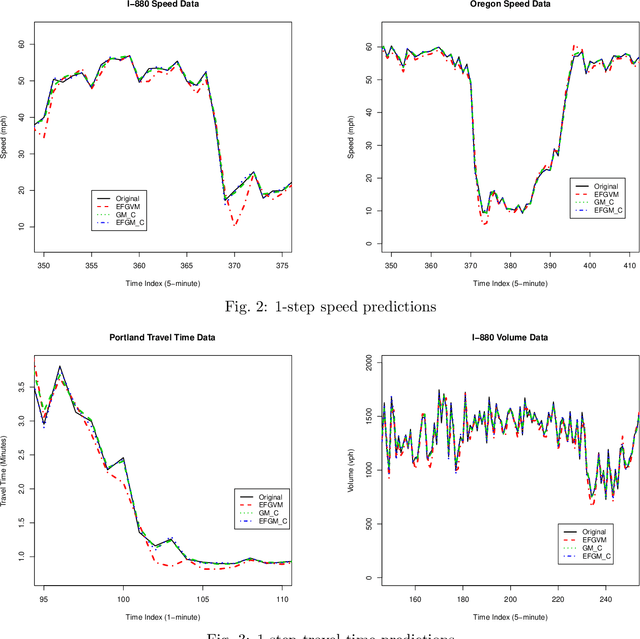
Abstract:In transportation applications such as real-time route guidance, ramp metering, congestion pricing and special events traffic management, accurate short-term traffic flow prediction is needed. For this purpose, this paper proposes several novel \textit{online} Grey system models (GM): GM(1,1$|cos(\omega t)$), GM(1,1$|sin(\omega t)$, $cos(\omega t)$), and GM(1,1$|e^{-at}$,$sin(\omega t)$,$cos(\omega t)$). To evaluate the performance of the proposed models, they are compared against a set of benchmark models: GM(1,1) model, Grey Verhulst models with and without Fourier error corrections, linear time series model, and nonlinear time series model. The evaluation is performed using loop detector and probe vehicle data from California, Virginia, and Oregon. Among the benchmark models, the error corrected Grey Verhulst model with Fourier outperformed the GM(1,1) model, linear time series, and non-linear time series models. In turn, the three proposed models, GM(1,1$|cos(\omega t)$), GM(1,1$|sin(\omega t)$,$cos(\omega t)$), and GM(1,1$|e^{-at}$,$sin(\omega t)$,$cos(\omega t)$), outperformed the Grey Verhulst model in prediction by at least $65\%$, $16\%$, and $11\%$, in terms of Root Mean Squared Error, and by $82\%$, $58\%$, and $42\%$, in terms of Mean Absolute Percentage Error, respectively. It is observed that the proposed Grey system models are more adaptive to location (e.g., perform well for all roadway types) and traffic parameters (e.g., speed, travel time, occupancy, and volume), and they do not require as many data points for training (4 observations are found to be sufficient).
Cycle-to-Cycle Queue Length Estimation from Connected Vehicles with Filtering on Primary Parameters
Nov 18, 2020
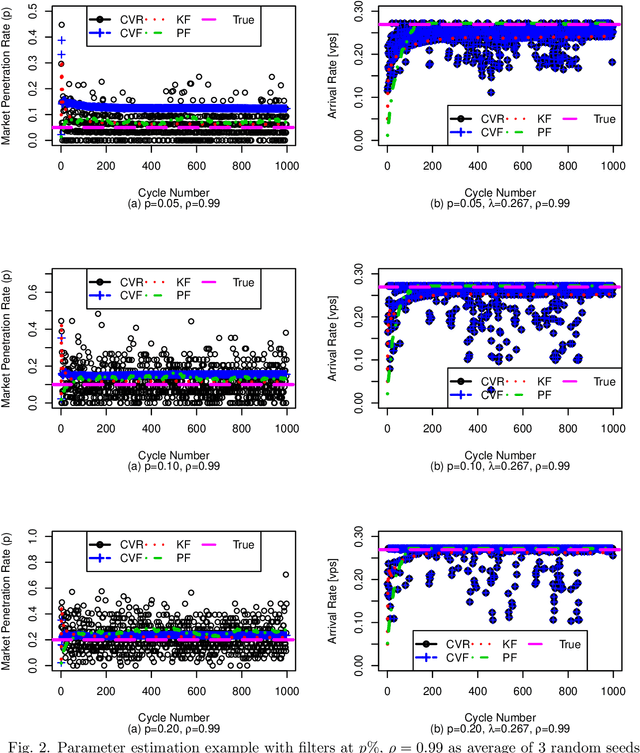

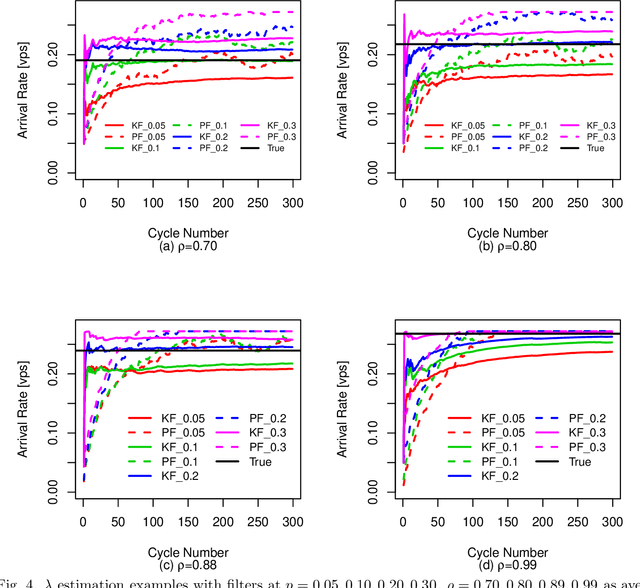
Abstract:Estimation models from connected vehicles often assume low level parameters such as arrival rates and market penetration rates as known or estimate them in real-time. At low market penetration rates, such parameter estimators produce large errors making estimated queue lengths inefficient for control or operations applications. In order to improve accuracy of low level parameter estimations, this study investigates the impact of connected vehicles information filtering on queue length estimation models. Filters are used as multilevel real-time estimators. Accuracy is tested against known arrival rate and market penetration rate scenarios using microsimulations. To understand the effectiveness for short-term or for dynamic processes, arrival rates, and market penetration rates are changed every 15 minutes. The results show that with Kalman and Particle filters, parameter estimators are able to find the true values within 15 minutes and meet and surpass the accuracy of known parameter scenarios especially for low market penetration rates. In addition, using last known estimated queue lengths when no connected vehicle is present performs better than inputting average estimated values. Moreover, the study shows that both filtering algorithms are suitable for real-time applications that require less than 0.1 second computational time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge