Bayesian Parameter Estimations for Grey System Models in Online Traffic Speed Predictions
Paper and Code
Aug 15, 2021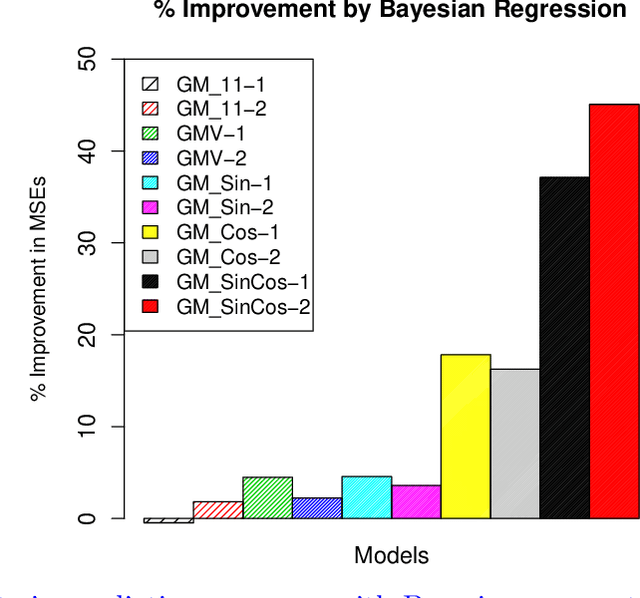
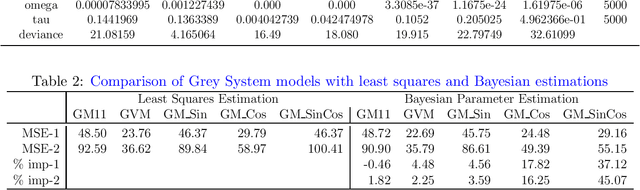
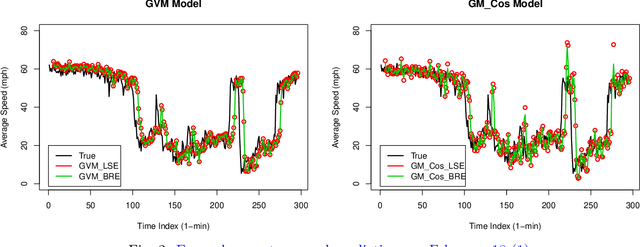
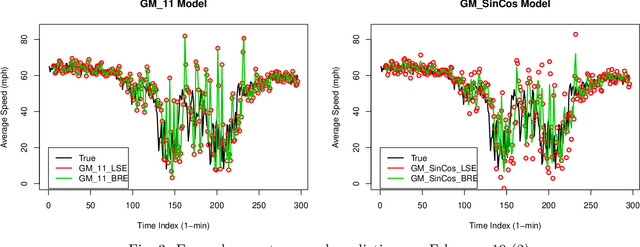
This paper presents Bayesian parameter estimation for first order Grey system models' parameters (or sometimes referred to as hyperparameters). There are different forms of first-order Grey System Models. These include $GM(1,1)$, $GM(1,1| \cos(\omega t)$, $GM(1,1| \sin(\omega t)$, and $GM(1,1| \cos(\omega t), \sin(\omega t)$. The whitenization equation of these models is a first-order linear differential equation of the form \[ \frac{dx}{dt} + a x = f(t) \] where $a$ is a parameter and $f(t) = b$ in $GM(1,1|)$ , $f(t) = b_1\cos(\omega t) + b_2$ in $GM(1,1| cos(\omega t)$, $f(t) = b_1\sin(\omega t)+b_2$ in $GM(1,1| \sin(\omega t)$, $f(t) = b_1\sin(\omega t) + b_2\cos(\omega t) + b_3$ in $GM(1,1| \cos(\omega t), \sin(\omega t)$, $f(t) = b x^2$ in Grey Verhulst model (GVM), and where $b, b_1, b_2$, and $b_3$ are parameters. The results from Bayesian estimations are compared to the least square estimated models with fixed $\omega$. We found that using rolling Bayesian estimations for GM parameters can allow us to estimate the parameters in all possible forms. Based on the data used for the comparison, the numerical results showed that models with Bayesian parameter estimations are up to 45\% more accurate in mean squared errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge