Improved Grey System Models for Predicting Traffic Parameters
Paper and Code
Nov 18, 2020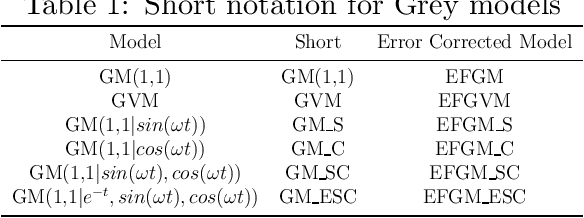
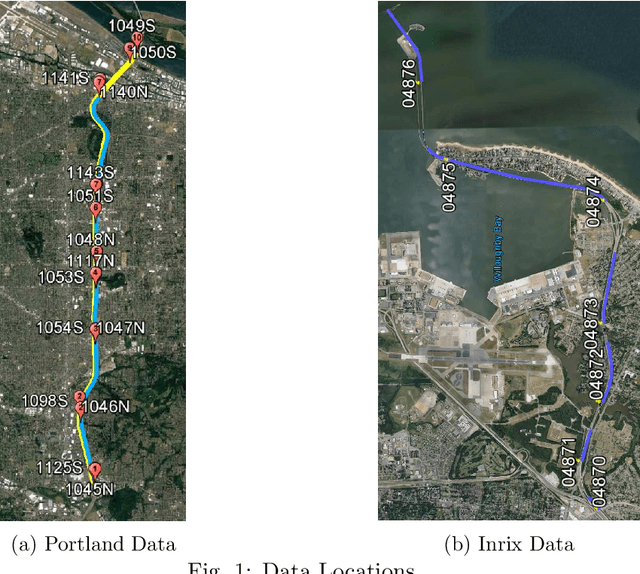
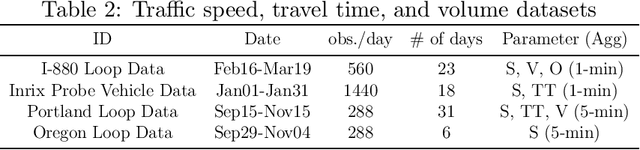
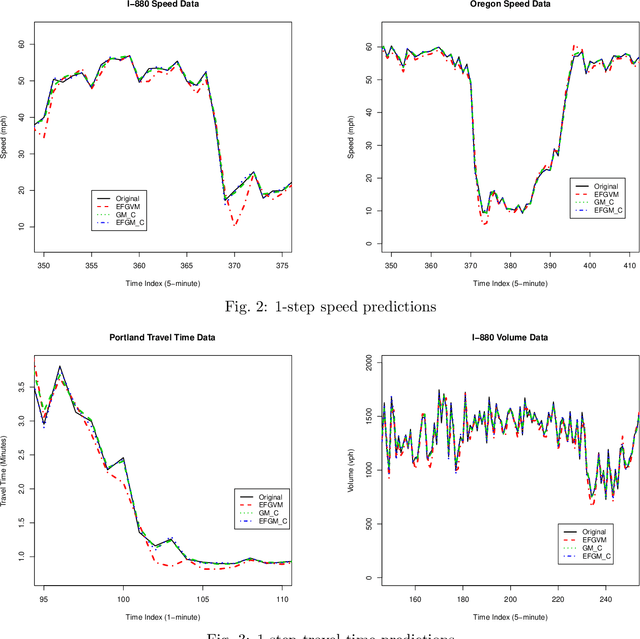
In transportation applications such as real-time route guidance, ramp metering, congestion pricing and special events traffic management, accurate short-term traffic flow prediction is needed. For this purpose, this paper proposes several novel \textit{online} Grey system models (GM): GM(1,1$|cos(\omega t)$), GM(1,1$|sin(\omega t)$, $cos(\omega t)$), and GM(1,1$|e^{-at}$,$sin(\omega t)$,$cos(\omega t)$). To evaluate the performance of the proposed models, they are compared against a set of benchmark models: GM(1,1) model, Grey Verhulst models with and without Fourier error corrections, linear time series model, and nonlinear time series model. The evaluation is performed using loop detector and probe vehicle data from California, Virginia, and Oregon. Among the benchmark models, the error corrected Grey Verhulst model with Fourier outperformed the GM(1,1) model, linear time series, and non-linear time series models. In turn, the three proposed models, GM(1,1$|cos(\omega t)$), GM(1,1$|sin(\omega t)$,$cos(\omega t)$), and GM(1,1$|e^{-at}$,$sin(\omega t)$,$cos(\omega t)$), outperformed the Grey Verhulst model in prediction by at least $65\%$, $16\%$, and $11\%$, in terms of Root Mean Squared Error, and by $82\%$, $58\%$, and $42\%$, in terms of Mean Absolute Percentage Error, respectively. It is observed that the proposed Grey system models are more adaptive to location (e.g., perform well for all roadway types) and traffic parameters (e.g., speed, travel time, occupancy, and volume), and they do not require as many data points for training (4 observations are found to be sufficient).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge