PRS: Sharp Feature Priors for Resolution-Free Surface Remeshing

Surface reconstruction with preservation of geometric features is a challenging computer vision task. Despite significant progress in implicit shape reconstruction, state-of-the-art mesh extraction methods often produce aliased, perceptually distorted surfaces and lack scalability to high-resolution 3D shapes. We present a data-driven approach for automatic feature detection and remeshing that requires only a coarse, aliased mesh as input and scales to arbitrary resolution reconstructions. We define and learn a collection of surface-based fields to (1) capture sharp geometric features in the shape with an implicit vertexwise model and (2) approximate improvements in normals alignment obtained by applying edge-flips with an edgewise model. To support scaling to arbitrary complexity shapes, we learn our fields using local triangulated patches, fusing estimates on complete surface meshes. Our feature remeshing algorithm integrates the learned fields as sharp feature priors and optimizes vertex placement and mesh connectivity for maximum expected surface improvement. On a challenging collection of high-resolution shape reconstructions in the ABC dataset, our algorithm improves over state-of-the-art by 26% normals F-score and 42% perceptual $\text{RMSE}_{\text{v}}$.

GAN Path Finder: Preliminary results

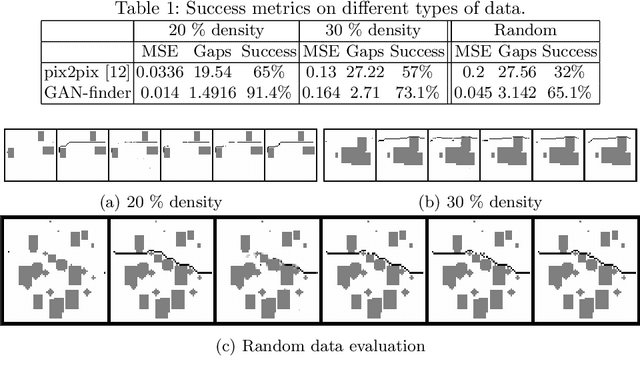
2D path planning in static environment is a well-known problem and one of the common ways to solve it is to 1) represent the environment as a grid and 2) perform a heuristic search for a path on it. At the same time 2D grid resembles much a digital image, thus an appealing idea comes to being -- to treat the problem as an image generation task and to solve it utilizing the recent advances in deep learning. In this work we make an attempt to apply a generative neural network as a path finder and report preliminary results, convincing enough to claim that this direction of research is worth further exploration.

eLIAN: Enhanced Algorithm for Angle-constrained Path Finding

Problem of finding 2D paths of special shape, e.g. paths comprised of line segments having the property that the angle between any two consecutive segments does not exceed the predefined threshold, is considered in the paper. This problem is harder to solve than the one when shortest paths of any shape are sought, since the planer's search space is substantially bigger as multiple search nodes corresponding to the same location need to be considered. One way to reduce the search effort is to fix the length of the path's segment and to prune the nodes that violate the imposed constraint. This leads to incompleteness and to the sensitivity of the 's performance to chosen parameter value. In this work we introduce a novel technique that reduces this sensitivity by automatically adjusting the length of the path's segment on-the-fly, e.g. during the search. Embedding this technique into the known grid-based angle-constrained path finding algorithm - LIAN, leads to notable increase of the planner's effectiveness, e.g. success rate, while keeping efficiency, e.g. runtime, overhead at reasonable level. Experimental evaluation shows that LIAN with the suggested enhancements, dubbed eLIAN, solves up to 20\% of tasks more compared to the predecessor. Meanwhile, the solution quality of eLIAN is nearly the same as the one of LIAN.