MAPF-GPT: Imitation Learning for Multi-Agent Pathfinding at Scale

Multi-agent pathfinding (MAPF) is a challenging computational problem that typically requires to find collision-free paths for multiple agents in a shared environment. Solving MAPF optimally is NP-hard, yet efficient solutions are critical for numerous applications, including automated warehouses and transportation systems. Recently, learning-based approaches to MAPF have gained attention, particularly those leveraging deep reinforcement learning. Following current trends in machine learning, we have created a foundation model for the MAPF problems called MAPF-GPT. Using imitation learning, we have trained a policy on a set of pre-collected sub-optimal expert trajectories that can generate actions in conditions of partial observability without additional heuristics, reward functions, or communication with other agents. The resulting MAPF-GPT model demonstrates zero-shot learning abilities when solving the MAPF problem instances that were not present in the training dataset. We show that MAPF-GPT notably outperforms the current best-performing learnable-MAPF solvers on a diverse range of problem instances and is efficient in terms of computation (in the inference mode).

POGEMA: A Benchmark Platform for Cooperative Multi-Agent Navigation

Multi-agent reinforcement learning (MARL) has recently excelled in solving challenging cooperative and competitive multi-agent problems in various environments with, mostly, few agents and full observability. Moreover, a range of crucial robotics-related tasks, such as multi-robot navigation and obstacle avoidance, that have been conventionally approached with the classical non-learnable methods (e.g., heuristic search) is currently suggested to be solved by the learning-based or hybrid methods. Still, in this domain, it is hard, not to say impossible, to conduct a fair comparison between classical, learning-based, and hybrid approaches due to the lack of a unified framework that supports both learning and evaluation. To this end, we introduce POGEMA, a set of comprehensive tools that includes a fast environment for learning, a generator of problem instances, the collection of pre-defined ones, a visualization toolkit, and a benchmarking tool that allows automated evaluation. We introduce and specify an evaluation protocol defining a range of domain-related metrics computed on the basics of the primary evaluation indicators (such as success rate and path length), allowing a fair multi-fold comparison. The results of such a comparison, which involves a variety of state-of-the-art MARL, search-based, and hybrid methods, are presented.

Optimal and Bounded Suboptimal Any-Angle Multi-agent Pathfinding

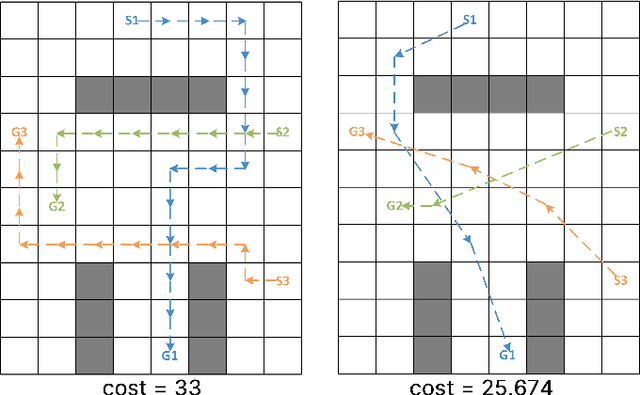
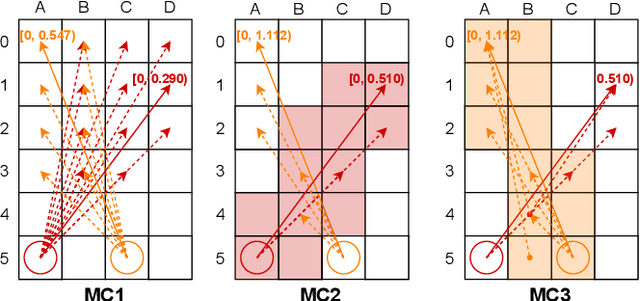
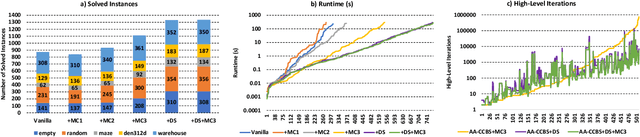
Multi-agent pathfinding (MAPF) is the problem of finding a set of conflict-free paths for a set of agents. Typically, the agents' moves are limited to a pre-defined graph of possible locations and allowed transitions between them, e.g. a 4-neighborhood grid. We explore how to solve MAPF problems when each agent can move between any pair of possible locations as long as traversing the line segment connecting them does not lead to the collision with the obstacles. This is known as any-angle pathfinding. We present the first optimal any-angle multi-agent pathfinding algorithm. Our planner is based on the Continuous Conflict-based Search (CCBS) algorithm and an optimal any-angle variant of the Safe Interval Path Planning (TO-AA-SIPP). The straightforward combination of those, however, scales poorly since any-angle path finding induces search trees with a very large branching factor. To mitigate this, we adapt two techniques from classical MAPF to the any-angle setting, namely Disjoint Splitting and Multi-Constraints. Experimental results on different combinations of these techniques show they enable solving over 30% more problems than the vanilla combination of CCBS and TO-AA-SIPP. In addition, we present a bounded-suboptimal variant of our algorithm, that enables trading runtime for solution cost in a controlled manner.

Decentralized Monte Carlo Tree Search for Partially Observable Multi-agent Pathfinding

The Multi-Agent Pathfinding (MAPF) problem involves finding a set of conflict-free paths for a group of agents confined to a graph. In typical MAPF scenarios, the graph and the agents' starting and ending vertices are known beforehand, allowing the use of centralized planning algorithms. However, in this study, we focus on the decentralized MAPF setting, where the agents may observe the other agents only locally and are restricted in communications with each other. Specifically, we investigate the lifelong variant of MAPF, where new goals are continually assigned to the agents upon completion of previous ones. Drawing inspiration from the successful AlphaZero approach, we propose a decentralized multi-agent Monte Carlo Tree Search (MCTS) method for MAPF tasks. Our approach utilizes the agent's observations to recreate the intrinsic Markov decision process, which is then used for planning with a tailored for multi-agent tasks version of neural MCTS. The experimental results show that our approach outperforms state-of-the-art learnable MAPF solvers. The source code is available at https://github.com/AIRI-Institute/mats-lp.

Learn to Follow: Decentralized Lifelong Multi-agent Pathfinding via Planning and Learning

Multi-agent Pathfinding (MAPF) problem generally asks to find a set of conflict-free paths for a set of agents confined to a graph and is typically solved in a centralized fashion. Conversely, in this work, we investigate the decentralized MAPF setting, when the central controller that posses all the information on the agents' locations and goals is absent and the agents have to sequientially decide the actions on their own without having access to a full state of the environment. We focus on the practically important lifelong variant of MAPF, which involves continuously assigning new goals to the agents upon arrival to the previous ones. To address this complex problem, we propose a method that integrates two complementary approaches: planning with heuristic search and reinforcement learning through policy optimization. Planning is utilized to construct and re-plan individual paths. We enhance our planning algorithm with a dedicated technique tailored to avoid congestion and increase the throughput of the system. We employ reinforcement learning to discover the collision avoidance policies that effectively guide the agents along the paths. The policy is implemented as a neural network and is effectively trained without any reward-shaping or external guidance. We evaluate our method on a wide range of setups comparing it to the state-of-the-art solvers. The results show that our method consistently outperforms the learnable competitors, showing higher throughput and better ability to generalize to the maps that were unseen at the training stage. Moreover our solver outperforms a rule-based one in terms of throughput and is an order of magnitude faster than a state-of-the-art search-based solver.

Monte-Carlo Tree Search for Multi-Agent Pathfinding: Preliminary Results

In this work we study a well-known and challenging problem of Multi-agent Pathfinding, when a set of agents is confined to a graph, each agent is assigned a unique start and goal vertices and the task is to find a set of collision-free paths (one for each agent) such that each agent reaches its respective goal. We investigate how to utilize Monte-Carlo Tree Search (MCTS) to solve the problem. Although MCTS was shown to demonstrate superior performance in a wide range of problems like playing antagonistic games (e.g. Go, Chess etc.), discovering faster matrix multiplication algorithms etc., its application to the problem at hand was not well studied before. To this end we introduce an original variant of MCTS, tailored to multi-agent pathfinding. The crux of our approach is how the reward, that guides MCTS, is computed. Specifically, we use individual paths to assist the agents with the the goal-reaching behavior, while leaving them freedom to get off the track if it is needed to avoid collisions. We also use a dedicated decomposition technique to reduce the branching factor of the tree search procedure. Empirically we show that the suggested method outperforms the baseline planning algorithm that invokes heuristic search, e.g. A*, at each re-planning step.

TransPath: Learning Heuristics For Grid-Based Pathfinding via Transformers

Heuristic search algorithms, e.g. A*, are the commonly used tools for pathfinding on grids, i.e. graphs of regular structure that are widely employed to represent environments in robotics, video games etc. Instance-independent heuristics for grid graphs, e.g. Manhattan distance, do not take the obstacles into account and, thus, the search led by such heuristics performs poorly in the obstacle-rich environments. To this end, we suggest learning the instance-dependent heuristic proxies that are supposed to notably increase the efficiency of the search. The first heuristic proxy we suggest to learn is the correction factor, i.e. the ratio between the instance independent cost-to-go estimate and the perfect one (computed offline at the training phase). Unlike learning the absolute values of the cost-to-go heuristic function, which was known before, when learning the correction factor the knowledge of the instance-independent heuristic is utilized. The second heuristic proxy is the path probability, which indicates how likely the grid cell is lying on the shortest path. This heuristic can be utilized in the Focal Search framework as the secondary heuristic, allowing us to preserve the guarantees on the bounded sub-optimality of the solution. We learn both suggested heuristics in a supervised fashion with the state-of-the-art neural networks containing attention blocks (transformers). We conduct a thorough empirical evaluation on a comprehensive dataset of planning tasks, showing that the suggested techniques i) reduce the computational effort of the A* up to a factor of $4$x while producing the solutions, which costs exceed the costs of the optimal solutions by less than $0.3$% on average; ii) outperform the competitors, which include the conventional techniques from the heuristic search, i.e. weighted A*, as well as the state-of-the-art learnable planners.

Analysis Of The Anytime MAPF Solvers Based On The Combination Of Conflict-Based Search and Focal Search

Conflict-Based Search (CBS) is a widely used algorithm for solving multi-agent pathfinding (MAPF) problems optimally. The core idea of CBS is to run hierarchical search, when, on the high level the tree of solutions candidates is explored, and on the low-level an individual planning for a specific agent (subject to certain constraints) is carried out. To trade-off optimality for running time different variants of bounded sub-optimal CBS were designed, which alter both high- and low-level search routines of CBS. Moreover, anytime variant of CBS does exist that applies Focal Search (FS) to the high-level of CBS - Anytime BCBS. However, no comprehensive analysis of how well this algorithm performs compared to the naive one, when we simply re-invoke CBS with the decreased sub-optimality bound, was present. This work aims at filling this gap. Moreover, we present and evaluate another anytime version of CBS that uses FS on both levels of CBS. Empirically, we show that its behavior is principally different from the one demonstrated by Anytime BCBS. Finally, we compare both algorithms head-to-head and show that using Focal Search on both levels of CBS can be beneficial in a wide range of setups.

POGEMA: Partially Observable Grid Environment for Multiple Agents

We introduce POGEMA (https://github.com/AIRI-Institute/pogema) a sandbox for challenging partially observable multi-agent pathfinding (PO-MAPF) problems . This is a grid-based environment that was specifically designed to be a flexible, tunable and scalable benchmark. It can be tailored to a variety of PO-MAPF, which can serve as an excellent testing ground for planning and learning methods, and their combination, which will allow us to move towards filling the gap between AI planning and learning.

Towards Time-Optimal Any-Angle Path Planning With Dynamic Obstacles

Path finding is a well-studied problem in AI, which is often framed as graph search. Any-angle path finding is a technique that augments the initial graph with additional edges to build shorter paths to the goal. Indeed, optimal algorithms for any-angle path finding in static environments exist. However, when dynamic obstacles are present and time is the objective to be minimized, these algorithms can no longer guarantee optimality. In this work, we elaborate on why this is the case and what techniques can be used to solve the problem optimally. We present two algorithms, grounded in the same idea, that can obtain provably optimal solutions to the considered problem. One of them is a naive algorithm and the other one is much more involved. We conduct a thorough empirical evaluation showing that, in certain setups, the latter algorithm might be as fast as the previously-known greedy non-optimal solver while providing solutions of better quality. In some (rare) cases, the difference in cost is up to 76%, while on average it is lower than one percent (the same cost difference is typically observed between optimal and greedy any-angle solvers in static environments).