Cause-effect inference through spectral independence in linear dynamical systems: theoretical foundations

Distinguishing between cause and effect using time series observational data is a major challenge in many scientific fields. A new perspective has been provided based on the principle of Independence of Causal Mechanisms (ICM), leading to the Spectral Independence Criterion (SIC), postulating that the power spectral density (PSD) of the cause time series is uncorrelated with the squared modulus of the frequency response of the filter generating the effect. Since SIC rests on methods and assumptions in stark contrast with most causal discovery methods for time series, it raises questions regarding what theoretical grounds justify its use. In this paper, we provide answers covering several key aspects. After providing an information theoretic interpretation of SIC, we present an identifiability result that sheds light on the context for which this approach is expected to perform well. We further demonstrate the robustness of SIC to downsampling - an obstacle that can spoil Granger-based inference. Finally, an invariance perspective allows to explore the limitations of the spectral independence assumption and how to generalize it. Overall, these results support the postulate of Spectral Independence is a well grounded leading principle for causal inference based on empirical time series.

Learning from Positive and Unlabeled Data by Identifying the Annotation Process

In binary classification, Learning from Positive and Unlabeled data (LePU) is semi-supervised learning but with labeled elements from only one class. Most of the research on LePU relies on some form of independence between the selection process of annotated examples and the features of the annotated class, known as the Selected Completely At Random (SCAR) assumption. Yet the annotation process is an important part of the data collection, and in many cases it naturally depends on certain features of the data (e.g., the intensity of an image and the size of the object to be detected in the image). Without any constraints on the model for the annotation process, classification results in the LePU problem will be highly non-unique. So proper, flexible constraints are needed. In this work we incorporate more flexible and realistic models for the annotation process than SCAR, and more importantly, offer a solution for the challenging LePU problem. On the theory side, we establish the identifiability of the properties of the annotation process and the classification function, in light of the considered constraints on the data-generating process. We also propose an inference algorithm to learn the parameters of the model, with successful experimental results on both simulated and real data. We also propose a novel real-world dataset forLePU, as a benchmark dataset for future studies.

Group invariance principles for causal generative models

The postulate of independence of cause and mechanism (ICM) has recently led to several new causal discovery algorithms. The interpretation of independence and the way it is utilized, however, varies across these methods. Our aim in this paper is to propose a group theoretic framework for ICM to unify and generalize these approaches. In our setting, the cause-mechanism relationship is assessed by comparing it against a null hypothesis through the application of random generic group transformations. We show that the group theoretic view provides a very general tool to study the structure of data generating mechanisms with direct applications to machine learning.

Telling cause from effect in deterministic linear dynamical systems

Inferring a cause from its effect using observed time series data is a major challenge in natural and social sciences. Assuming the effect is generated by the cause trough a linear system, we propose a new approach based on the hypothesis that nature chooses the "cause" and the "mechanism that generates the effect from the cause" independent of each other. We therefore postulate that the power spectrum of the time series being the cause is uncorrelated with the square of the transfer function of the linear filter generating the effect. While most causal discovery methods for time series mainly rely on the noise, our method relies on asymmetries of the power spectral density properties that can be exploited even in the context of deterministic systems. We describe mathematical assumptions in a deterministic model under which the causal direction is identifiable with this approach. We also discuss the method's performance under the additive noise model and its relationship to Granger causality. Experiments show encouraging results on synthetic as well as real-world data. Overall, this suggests that the postulate of Independence of Cause and Mechanism is a promising principle for causal inference on empirical time series.

Justifying Information-Geometric Causal Inference

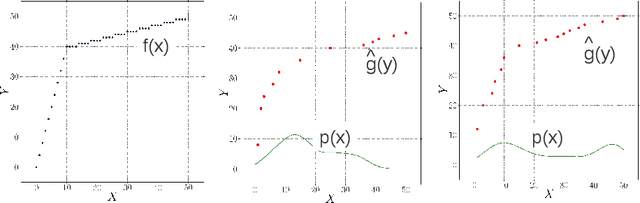
Information Geometric Causal Inference (IGCI) is a new approach to distinguish between cause and effect for two variables. It is based on an independence assumption between input distribution and causal mechanism that can be phrased in terms of orthogonality in information space. We describe two intuitive reinterpretations of this approach that makes IGCI more accessible to a broader audience. Moreover, we show that the described independence is related to the hypothesis that unsupervised learning and semi-supervised learning only works for predicting the cause from the effect and not vice versa.