Justifying Information-Geometric Causal Inference

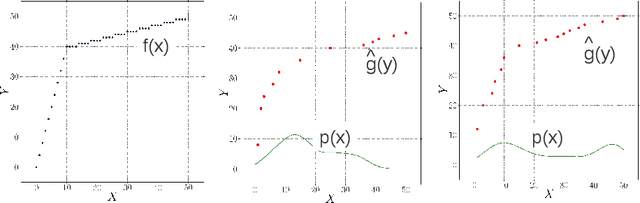
Information Geometric Causal Inference (IGCI) is a new approach to distinguish between cause and effect for two variables. It is based on an independence assumption between input distribution and causal mechanism that can be phrased in terms of orthogonality in information space. We describe two intuitive reinterpretations of this approach that makes IGCI more accessible to a broader audience. Moreover, we show that the described independence is related to the hypothesis that unsupervised learning and semi-supervised learning only works for predicting the cause from the effect and not vice versa.