Cooperative Multi-Agent Path Finding: Beyond Path Planning and Collision Avoidance

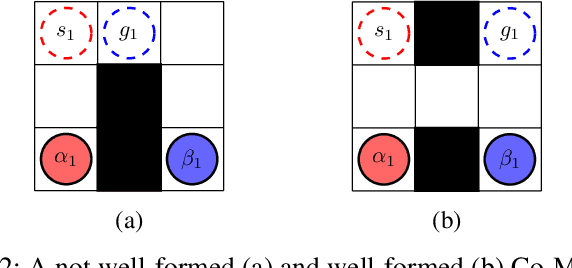
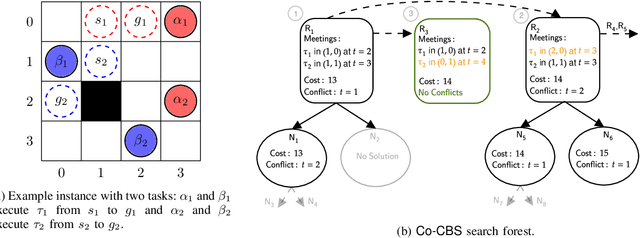
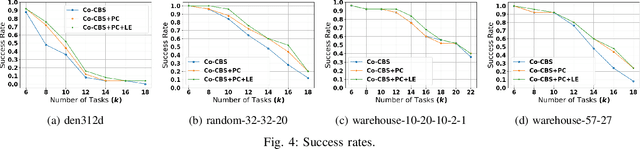
We introduce the Cooperative Multi-Agent Path Finding (Co-MAPF) problem, an extension to the classical MAPF problem, where cooperative behavior is incorporated. In this setting, a group of autonomous agents operate in a shared environment and have to complete cooperative tasks while avoiding collisions with the other agents in the group. This extension naturally models many real-world applications, where groups of agents are required to collaborate in order to complete a given task. To this end, we formalize the Co-MAPF problem and introduce Cooperative Conflict-Based Search (Co-CBS), a CBS-based algorithm for solving the problem optimally for a wide set of Co-MAPF problems. Co-CBS uses a cooperation-planning module integrated into CBS such that cooperation planning is decoupled from path planning. Finally, we present empirical results on several MAPF benchmarks demonstrating our algorithm's properties.

ILS-SUMM: Iterated Local Search for Unsupervised Video Summarization

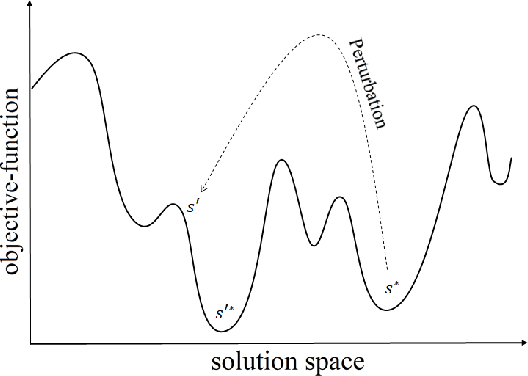
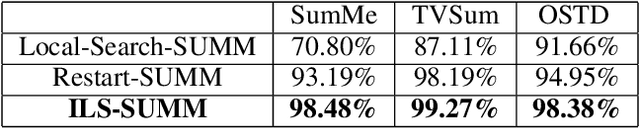
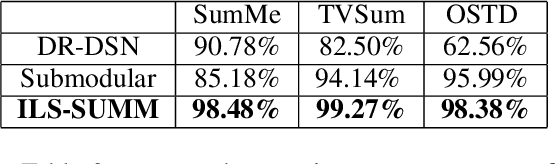
In recent years, there has been an increasing interest in building video summarization tools, where the goal is to automatically create a short summary of an input video that properly represents the original content. We consider shot-based video summarization where the summary consists of a subset of the video shots which can be of various lengths. A straightforward approach to maximize the representativeness of a subset of shots is by minimizing the total distance between shots and their nearest selected shots. We formulate the task of video summarization as an optimization problem with a knapsack-like constraint on the total summary duration. Previous studies have proposed greedy algorithms to solve this problem approximately, but no experiments were presented to measure the ability of these methods to obtain solutions with low total distance. Indeed, our experiments on video summarization datasets show that the success of current methods in obtaining results with low total distance still has much room for improvement. In this paper, we develop ILS-SUMM, a novel video summarization algorithm to solve the subset selection problem under the knapsack constraint. Our algorithm is based on the well-known metaheuristic optimization framework -- Iterated Local Search (ILS), known for its ability to avoid weak local minima and obtain a good near-global minimum. Extensive experiments show that our method finds solutions with significantly better total distance than previous methods. Moreover, to indicate the high scalability of ILS-SUMM, we introduce a new dataset consisting of videos of various lengths.

Learning Control for Air Hockey Striking using Deep Reinforcement Learning

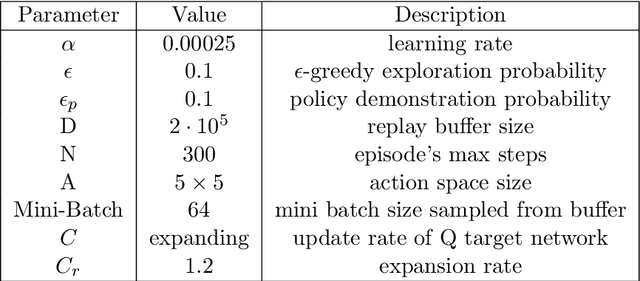
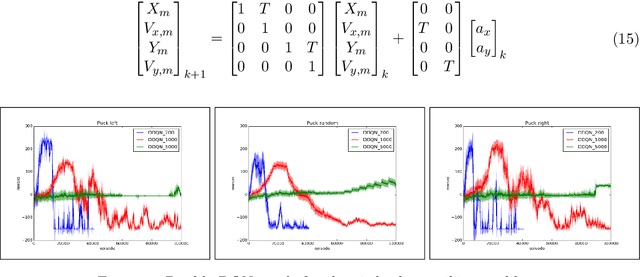
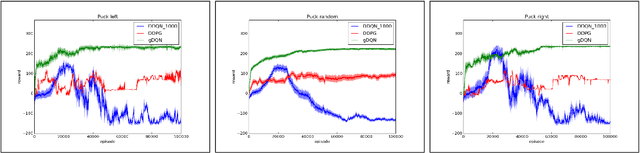
We consider the task of learning control policies for a robotic mechanism striking a puck in an air hockey game. The control signal is a direct command to the robot's motors. We employ a model free deep reinforcement learning framework to learn the motoric skills of striking the puck accurately in order to score. We propose certain improvements to the standard learning scheme which make the deep Q-learning algorithm feasible when it might otherwise fail. Our improvements include integrating prior knowledge into the learning scheme, and accounting for the changing distribution of samples in the experience replay buffer. Finally we present our simulation results for aimed striking which demonstrate the successful learning of this task, and the improvement in algorithm stability due to the proposed modifications.

Averaged-DQN: Variance Reduction and Stabilization for Deep Reinforcement Learning

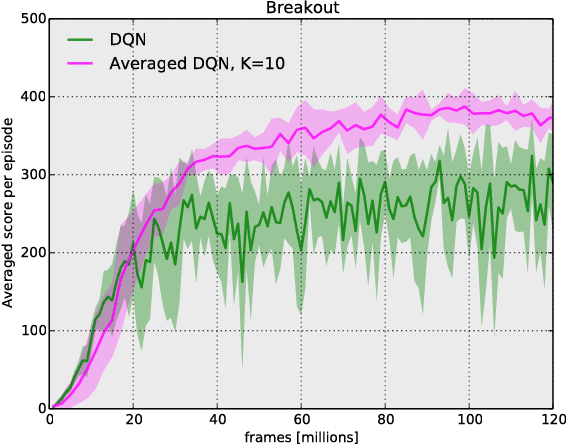
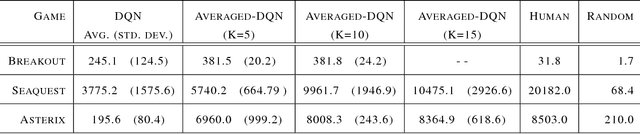
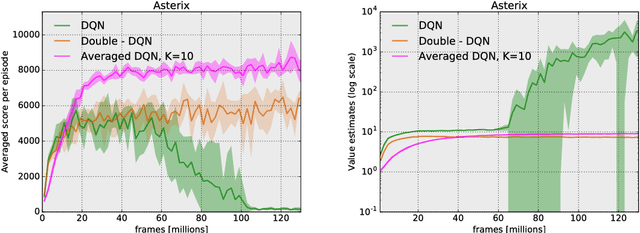
Instability and variability of Deep Reinforcement Learning (DRL) algorithms tend to adversely affect their performance. Averaged-DQN is a simple extension to the DQN algorithm, based on averaging previously learned Q-values estimates, which leads to a more stable training procedure and improved performance by reducing approximation error variance in the target values. To understand the effect of the algorithm, we examine the source of value function estimation errors and provide an analytical comparison within a simplified model. We further present experiments on the Arcade Learning Environment benchmark that demonstrate significantly improved stability and performance due to the proposed extension.

The Max $K$-Armed Bandit: PAC Lower Bounds and Efficient Algorithms

We consider the Max $K$-Armed Bandit problem, where a learning agent is faced with several stochastic arms, each a source of i.i.d. rewards of unknown distribution. At each time step the agent chooses an arm, and observes the reward of the obtained sample. Each sample is considered here as a separate item with the reward designating its value, and the goal is to find an item with the highest possible value. Our basic assumption is a known lower bound on the {\em tail function} of the reward distributions. Under the PAC framework, we provide a lower bound on the sample complexity of any $(\epsilon,\delta)$-correct algorithm, and propose an algorithm that attains this bound up to logarithmic factors. We analyze the robustness of the proposed algorithm and in addition, we compare the performance of this algorithm to the variant in which the arms are not distinguishable by the agent and are chosen randomly at each stage. Interestingly, when the maximal rewards of the arms happen to be similar, the latter approach may provide better performance.

The Max $K$-Armed Bandit: A PAC Lower Bound and tighter Algorithms

We consider the Max $K$-Armed Bandit problem, where a learning agent is faced with several sources (arms) of items (rewards), and interested in finding the best item overall. At each time step the agent chooses an arm, and obtains a random real valued reward. The rewards of each arm are assumed to be i.i.d., with an unknown probability distribution that generally differs among the arms. Under the PAC framework, we provide lower bounds on the sample complexity of any $(\epsilon,\delta)$-correct algorithm, and propose algorithms that attain this bound up to logarithmic factors. We compare the performance of this multi-arm algorithms to the variant in which the arms are not distinguishable by the agent and are chosen randomly at each stage. Interestingly, when the maximal rewards of the arms happen to be similar, the latter approach may provide better performance.

An Online Convex Optimization Approach to Blackwell's Approachability

The notion of approachability in repeated games with vector payoffs was introduced by Blackwell in the 1950s, along with geometric conditions for approachability and corresponding strategies that rely on computing {\em steering directions} as projections from the current average payoff vector to the (convex) target set. Recently, Abernethy, Batlett and Hazan (2011) proposed a class of approachability algorithms that rely on the no-regret properties of Online Linear Programming for computing a suitable sequence of steering directions. This is first carried out for target sets that are convex cones, and then generalized to any convex set by embedding it in a higher-dimensional convex cone. In this paper we present a more direct formulation that relies on the support function of the set, along with suitable Online Convex Optimization algorithms, which leads to a general class of approachability algorithms. We further show that Blackwell's original algorithm and its convergence follow as a special case.

Response-Based Approachability and its Application to Generalized No-Regret Algorithms

Approachability theory, introduced by Blackwell (1956), provides fundamental results on repeated games with vector-valued payoffs, and has been usefully applied since in the theory of learning in games and to learning algorithms in the online adversarial setup. Given a repeated game with vector payoffs, a target set $S$ is approachable by a certain player (the agent) if he can ensure that the average payoff vector converges to that set no matter what his adversary opponent does. Blackwell provided two equivalent sets of conditions for a convex set to be approachable. The first (primary) condition is a geometric separation condition, while the second (dual) condition requires that the set be {\em non-excludable}, namely that for every mixed action of the opponent there exists a mixed action of the agent (a {\em response}) such that the resulting payoff vector belongs to $S$. Existing approachability algorithms rely on the primal condition and essentially require to compute at each stage a projection direction from a given point to $S$. In this paper, we introduce an approachability algorithm that relies on Blackwell's {\em dual} condition. Thus, rather than projection, the algorithm relies on computation of the response to a certain action of the opponent at each stage. The utility of the proposed algorithm is demonstrated by applying it to certain generalizations of the classical regret minimization problem, which include regret minimization with side constraints and regret minimization for global cost functions. In these problems, computation of the required projections is generally complex but a response is readily obtainable.