A Bayesian Approach to Online Planning

The combination of Monte Carlo tree search and neural networks has revolutionized online planning. As neural network approximations are often imperfect, we ask whether uncertainty estimates about the network outputs could be used to improve planning. We develop a Bayesian planning approach that facilitates such uncertainty quantification, inspired by classical ideas from the meta-reasoning literature. We propose a Thompson sampling based algorithm for searching the tree of possible actions, for which we prove the first (to our knowledge) finite time Bayesian regret bound, and propose an efficient implementation for a restricted family of posterior distributions. In addition we propose a variant of the Bayes-UCB method applied to trees. Empirically, we demonstrate that on the ProcGen Maze and Leaper environments, when the uncertainty estimates are accurate but the neural network output is inaccurate, our Bayesian approach searches the tree much more effectively. In addition, we investigate whether popular uncertainty estimation methods are accurate enough to yield significant gains in planning. Our code is available at: https://github.com/nirgreshler/bayesian-online-planning.

Cooperative Multi-Agent Path Finding: Beyond Path Planning and Collision Avoidance

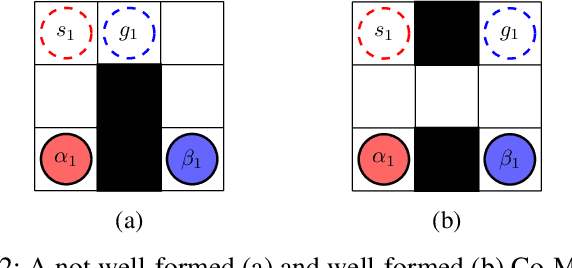
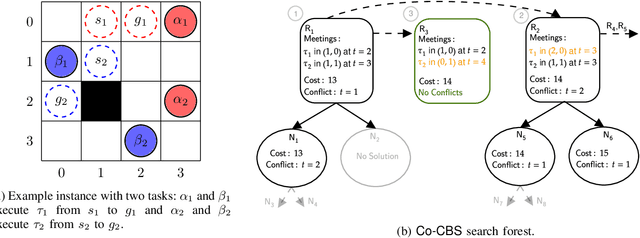
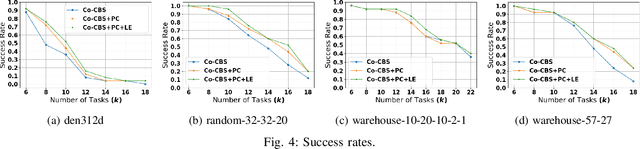
We introduce the Cooperative Multi-Agent Path Finding (Co-MAPF) problem, an extension to the classical MAPF problem, where cooperative behavior is incorporated. In this setting, a group of autonomous agents operate in a shared environment and have to complete cooperative tasks while avoiding collisions with the other agents in the group. This extension naturally models many real-world applications, where groups of agents are required to collaborate in order to complete a given task. To this end, we formalize the Co-MAPF problem and introduce Cooperative Conflict-Based Search (Co-CBS), a CBS-based algorithm for solving the problem optimally for a wide set of Co-MAPF problems. Co-CBS uses a cooperation-planning module integrated into CBS such that cooperation planning is decoupled from path planning. Finally, we present empirical results on several MAPF benchmarks demonstrating our algorithm's properties.