Mushir Akhtar
for the Alzheimer's Disease Neuroimaging
Twin Restricted Kernel Machines for Multiview Classification
Dec 12, 2025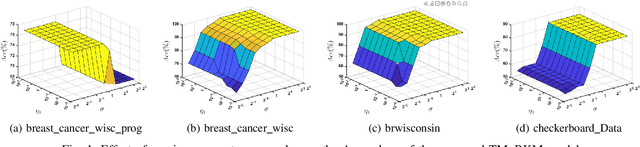
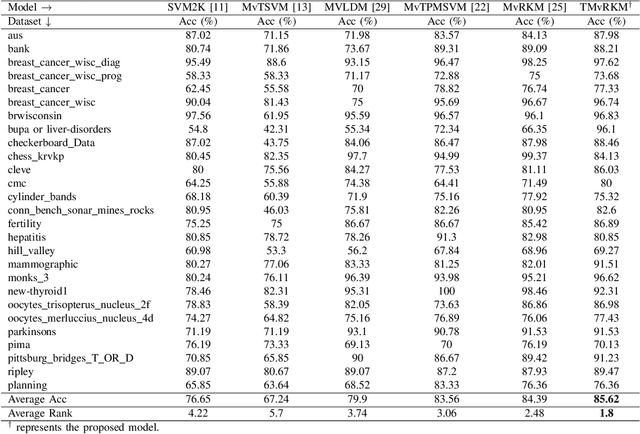
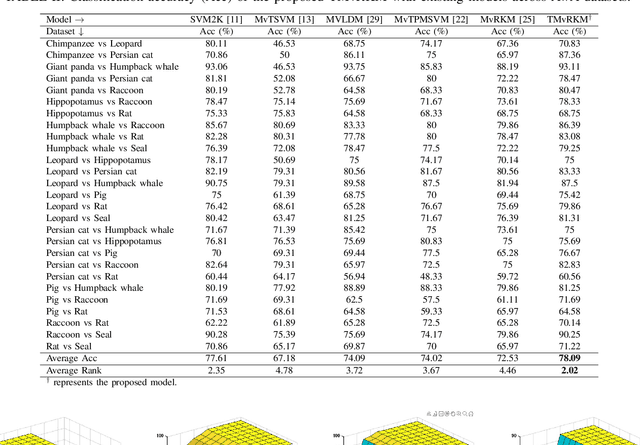
Abstract:Multi-view learning (MVL) is an emerging field in machine learning that focuses on improving generalization performance by leveraging complementary information from multiple perspectives or views. Various multi-view support vector machine (MvSVM) approaches have been developed, demonstrating significant success. Moreover, these models face challenges in effectively capturing decision boundaries in high-dimensional spaces using the kernel trick. They are also prone to errors and struggle with view inconsistencies, which are common in multi-view datasets. In this work, we introduce the multiview twin restricted kernel machine (TMvRKM), a novel model that integrates the strengths of kernel machines with the multiview framework, addressing key computational and generalization challenges associated with traditional kernel-based approaches. Unlike traditional methods that rely on solving large quadratic programming problems (QPPs), the proposed TMvRKM efficiently determines an optimal separating hyperplane through a regularized least squares approach, enhancing both computational efficiency and classification performance. The primal objective of TMvRKM includes a coupling term designed to balance errors across multiple views effectively. By integrating early and late fusion strategies, TMvRKM leverages the collective information from all views during training while remaining flexible to variations specific to individual views. The proposed TMvRKM model is rigorously tested on UCI, KEEL, and AwA benchmark datasets. Both experimental results and statistical analyses consistently highlight its exceptional generalization performance, outperforming baseline models in every scenario.
* pp. 1-8
R^2VFL: A Robust Random Vector Functional Link Network with Huber-Weighted Framework
Apr 29, 2025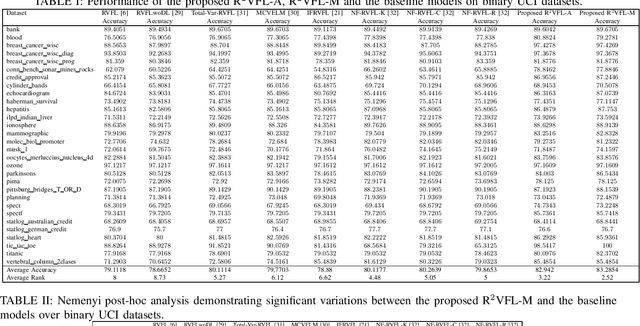
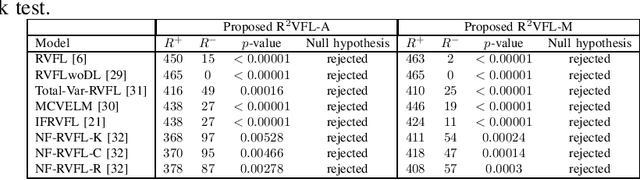
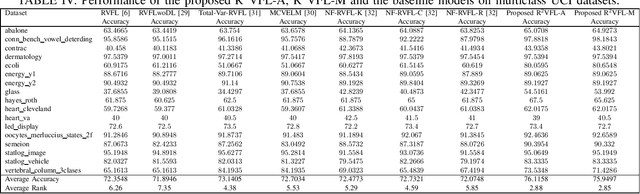
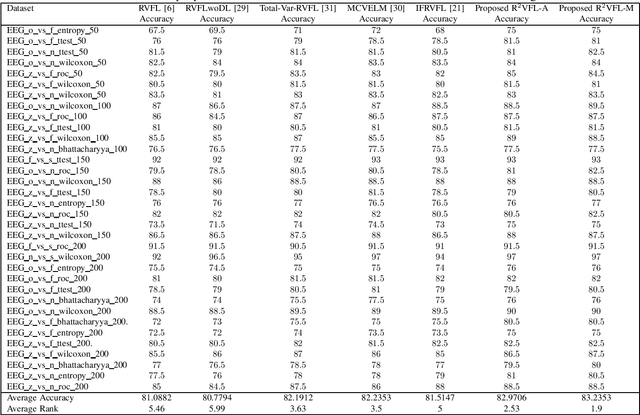
Abstract:The random vector functional link (RVFL) neural network has shown significant potential in overcoming the constraints of traditional artificial neural networks, such as excessive computation time and suboptimal solutions. However, RVFL faces challenges when dealing with noise and outliers, as it assumes all data samples contribute equally. To address this issue, we propose a novel robust framework, R2VFL, RVFL with Huber weighting function and class probability, which enhances the model's robustness and adaptability by effectively mitigating the impact of noise and outliers in the training data. The Huber weighting function reduces the influence of outliers, while the class probability mechanism assigns less weight to noisy data points, resulting in a more resilient model. We explore two distinct approaches for calculating class centers within the R2VFL framework: the simple average of all data points in each class and the median of each feature, the later providing a robust alternative by minimizing the effect of extreme values. These approaches give rise to two novel variants of the model-R2VFL-A and R2VFL-M. We extensively evaluate the proposed models on 47 UCI datasets, encompassing both binary and multiclass datasets, and conduct rigorous statistical testing, which confirms the superiority of the proposed models. Notably, the models also demonstrate exceptional performance in classifying EEG signals, highlighting their practical applicability in real-world biomedical domain.
CI-RKM: A Class-Informed Approach to Robust Restricted Kernel Machines
Apr 12, 2025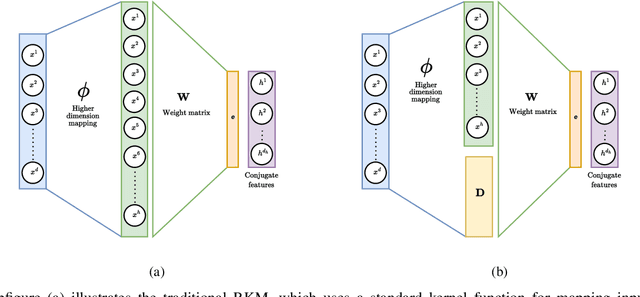
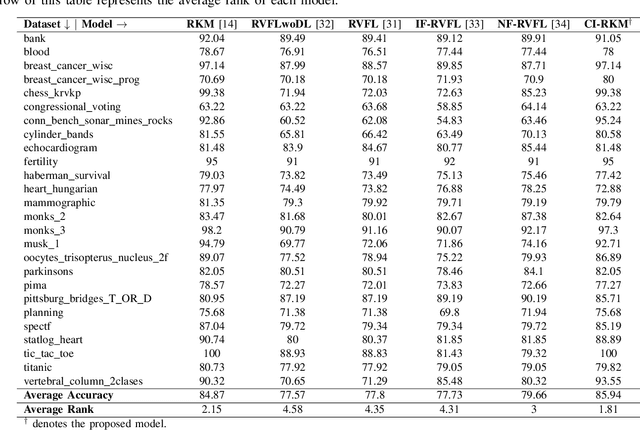
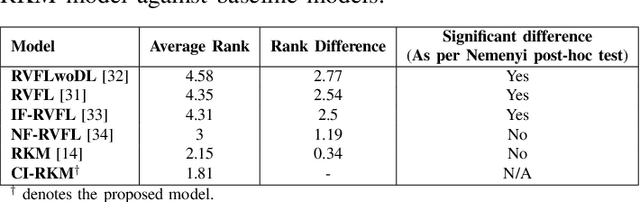
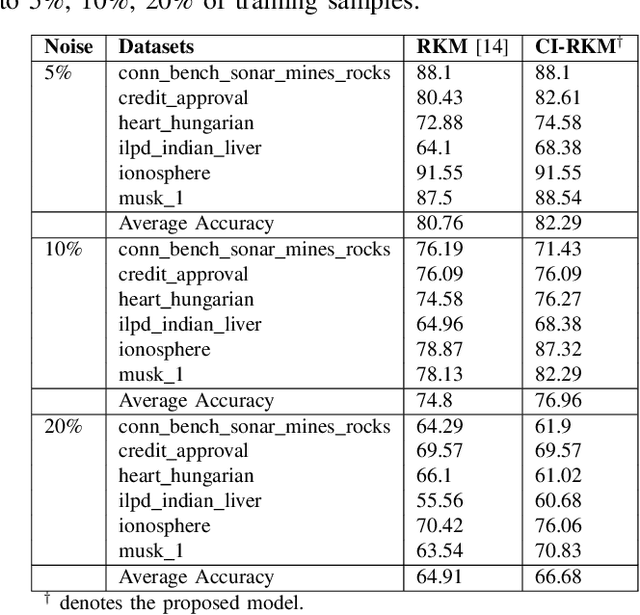
Abstract:Restricted kernel machines (RKMs) represent a versatile and powerful framework within the kernel machine family, leveraging conjugate feature duality to address a wide range of machine learning tasks, including classification, regression, and feature learning. However, their performance can degrade significantly in the presence of noise and outliers, which compromises robustness and predictive accuracy. In this paper, we propose a novel enhancement to the RKM framework by integrating a class-informed weighted function. This weighting mechanism dynamically adjusts the contribution of individual training points based on their proximity to class centers and class-specific characteristics, thereby mitigating the adverse effects of noisy and outlier data. By incorporating weighted conjugate feature duality and leveraging the Schur complement theorem, we introduce the class-informed restricted kernel machine (CI-RKM), a robust extension of the RKM designed to improve generalization and resilience to data imperfections. Experimental evaluations on benchmark datasets demonstrate that the proposed CI-RKM consistently outperforms existing baselines, achieving superior classification accuracy and enhanced robustness against noise and outliers. Our proposed method establishes a significant advancement in the development of kernel-based learning models, addressing a core challenge in the field.
Enhancing Imbalance Learning: A Novel Slack-Factor Fuzzy SVM Approach
Nov 26, 2024



Abstract:In real-world applications, class-imbalanced datasets pose significant challenges for machine learning algorithms, such as support vector machines (SVMs), particularly in effectively managing imbalance, noise, and outliers. Fuzzy support vector machines (FSVMs) address class imbalance by assigning varying fuzzy memberships to samples; however, their sensitivity to imbalanced datasets can lead to inaccurate assessments. The recently developed slack-factor-based FSVM (SFFSVM) improves traditional FSVMs by using slack factors to adjust fuzzy memberships based on misclassification likelihood, thereby rectifying misclassifications induced by the hyperplane obtained via different error cost (DEC). Building on SFFSVM, we propose an improved slack-factor-based FSVM (ISFFSVM) that introduces a novel location parameter. This novel parameter significantly advances the model by constraining the DEC hyperplane's extension, thereby mitigating the risk of misclassifying minority class samples. It ensures that majority class samples with slack factor scores approaching the location threshold are assigned lower fuzzy memberships, which enhances the model's discrimination capability. Extensive experimentation on a diverse array of real-world KEEL datasets demonstrates that the proposed ISFFSVM consistently achieves higher F1-scores, Matthews correlation coefficients (MCC), and area under the precision-recall curve (AUC-PR) compared to baseline classifiers. Consequently, the introduction of the location parameter, coupled with the slack-factor-based fuzzy membership, enables ISFFSVM to outperform traditional approaches, particularly in scenarios characterized by severe class disparity. The code for the proposed model is available at \url{https://github.com/mtanveer1/ISFFSVM}.
Flexi-Fuzz least squares SVM for Alzheimer's diagnosis: Tackling noise, outliers, and class imbalance
Oct 18, 2024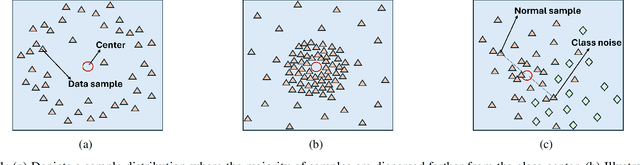
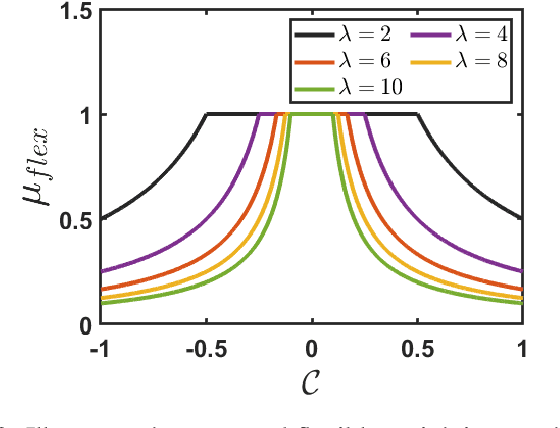


Abstract:Alzheimer's disease (AD) is a leading neurodegenerative condition and the primary cause of dementia, characterized by progressive cognitive decline and memory loss. Its progression, marked by shrinkage in the cerebral cortex, is irreversible. Numerous machine learning algorithms have been proposed for the early diagnosis of AD. However, they often struggle with the issues of noise, outliers, and class imbalance. To tackle the aforementioned limitations, in this article, we introduce a novel, robust, and flexible membership scheme called Flexi-Fuzz. This scheme integrates a novel flexible weighting mechanism, class probability, and imbalance ratio. The proposed flexible weighting mechanism assigns the maximum weight to samples within a specific proximity to the center, with a gradual decrease in weight beyond a certain threshold. This approach ensures that samples near the class boundary still receive significant weight, maintaining their influence in the classification process. Class probability is used to mitigate the impact of noisy samples, while the imbalance ratio addresses class imbalance. Leveraging this, we incorporate the proposed Flexi-Fuzz membership scheme into the least squares support vector machines (LSSVM) framework, resulting in a robust and flexible model termed Flexi-Fuzz-LSSVM. We determine the class-center using two methods: the conventional mean approach and an innovative median approach, leading to two model variants, Flexi-Fuzz-LSSVM-I and Flexi-Fuzz-LSSVM-II. To validate the effectiveness of the proposed Flexi-Fuzz-LSSVM models, we evaluated them on benchmark UCI and KEEL datasets, both with and without label noise. Additionally, we tested the models on the Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset for AD diagnosis. Experimental results demonstrate the superiority of the Flexi-Fuzz-LSSVM models over baseline models.
Enhanced Feature Based Granular Ball Twin Support Vector Machine
Oct 08, 2024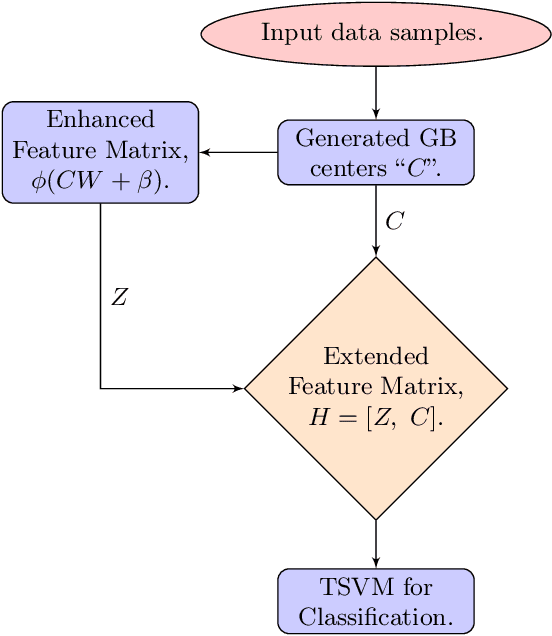



Abstract:In this paper, we propose enhanced feature based granular ball twin support vector machine (EF-GBTSVM). EF-GBTSVM employs the coarse granularity of granular balls (GBs) as input rather than individual data samples. The GBs are mapped to the feature space of the hidden layer using random projection followed by the utilization of a non-linear activation function. The concatenation of original and hidden features derived from the centers of GBs gives rise to an enhanced feature space, commonly referred to as the random vector functional link (RVFL) space. This space encapsulates nuanced feature information to GBs. Further, we employ twin support vector machine (TSVM) in the RVFL space for classification. TSVM generates the two non-parallel hyperplanes in the enhanced feature space, which improves the generalization performance of the proposed EF-GBTSVM model. Moreover, the coarser granularity of the GBs enables the proposed EF-GBTSVM model to exhibit robustness to resampling, showcasing reduced susceptibility to the impact of noise and outliers. We undertake a thorough evaluation of the proposed EF-GBTSVM model on benchmark UCI and KEEL datasets. This evaluation encompasses scenarios with and without the inclusion of label noise. Moreover, experiments using NDC datasets further emphasize the proposed model's ability to handle large datasets. Experimental results, supported by thorough statistical analyses, demonstrate that the proposed EF-GBTSVM model significantly outperforms the baseline models in terms of generalization capabilities, scalability, and robustness. The source code for the proposed EF-GBTSVM model, along with additional results and further details, can be accessed at https://github.com/mtanveer1/EF-GBTSVM.
Advancing RVFL networks: Robust classification with the HawkEye loss function
Oct 01, 2024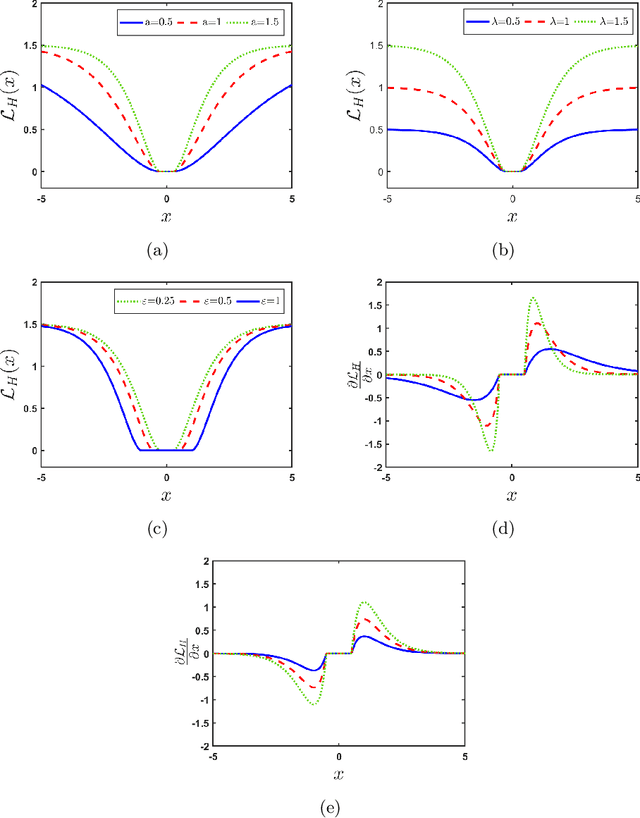

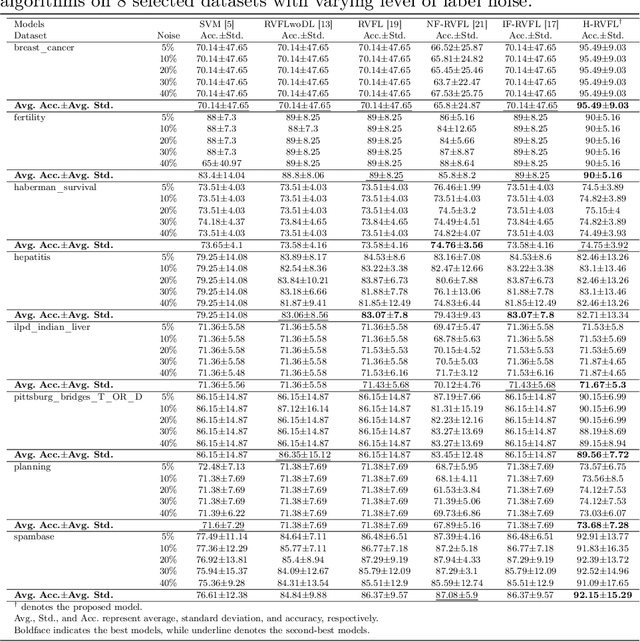
Abstract:Random vector functional link (RVFL), a variant of single-layer feedforward neural network (SLFN), has garnered significant attention due to its lower computational cost and robustness to overfitting. Despite its advantages, the RVFL network's reliance on the square error loss function makes it highly sensitive to outliers and noise, leading to degraded model performance in real-world applications. To remedy it, we propose the incorporation of the HawkEye loss (H-loss) function into the RVFL framework. The H-loss function features nice mathematical properties, including smoothness and boundedness, while simultaneously incorporating an insensitive zone. Each characteristic brings its own advantages: 1) Boundedness limits the impact of extreme errors, enhancing robustness against outliers; 2) Smoothness facilitates the use of gradient-based optimization algorithms, ensuring stable and efficient convergence; and 3) The insensitive zone mitigates the effect of minor discrepancies and noise. Leveraging the H-loss function, we embed it into the RVFL framework and develop a novel robust RVFL model termed H-RVFL. Notably, this work addresses a significant gap, as no bounded loss function has been incorporated into RVFL to date. The non-convex optimization of the proposed H-RVFL is effectively addressed by the Nesterov accelerated gradient (NAG) algorithm, whose computational complexity is also discussed. The proposed H-RVFL model's effectiveness is validated through extensive experiments on $40$ benchmark datasets from UCI and KEEL repositories, with and without label noise. The results highlight significant improvements in robustness and efficiency, establishing the H-RVFL model as a powerful tool for applications in noisy and outlier-prone environments.
GL-TSVM: A robust and smooth twin support vector machine with guardian loss function
Aug 29, 2024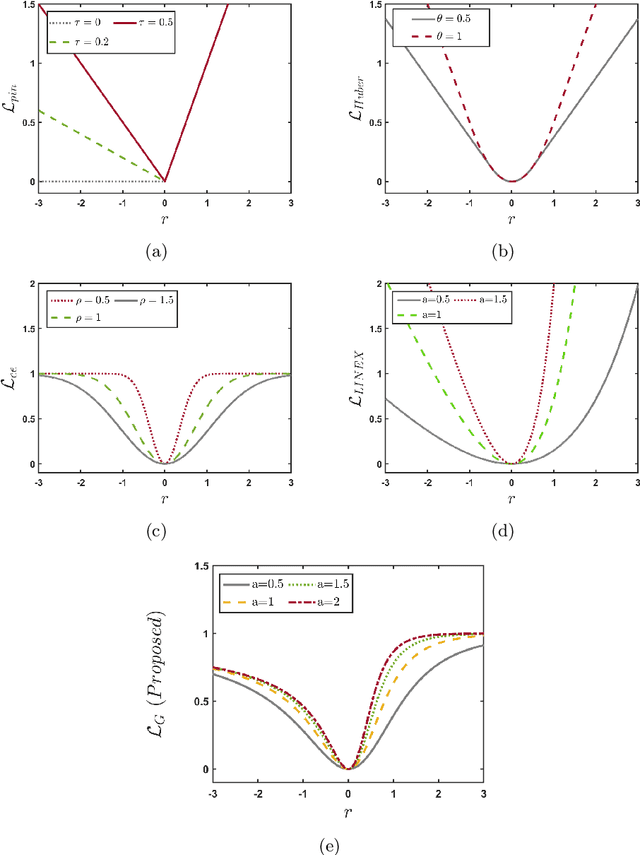
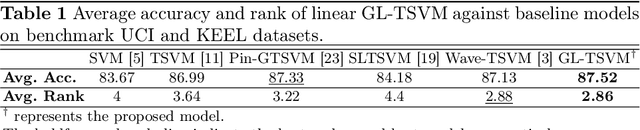
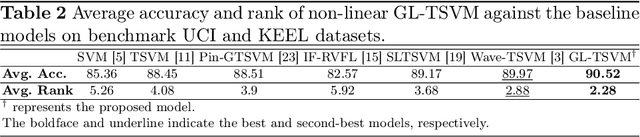

Abstract:Twin support vector machine (TSVM), a variant of support vector machine (SVM), has garnered significant attention due to its $3/4$ times lower computational complexity compared to SVM. However, due to the utilization of the hinge loss function, TSVM is sensitive to outliers or noise. To remedy it, we introduce the guardian loss (G-loss), a novel loss function distinguished by its asymmetric, bounded, and smooth characteristics. We then fuse the proposed G-loss function into the TSVM and yield a robust and smooth classifier termed GL-TSVM. Further, to adhere to the structural risk minimization (SRM) principle and reduce overfitting, we incorporate a regularization term into the objective function of GL-TSVM. To address the optimization challenges of GL-TSVM, we devise an efficient iterative algorithm. The experimental analysis on UCI and KEEL datasets substantiates the effectiveness of the proposed GL-TSVM in comparison to the baseline models. Moreover, to showcase the efficacy of the proposed GL-TSVM in the biomedical domain, we evaluated it on the breast cancer (BreaKHis) and schizophrenia datasets. The outcomes strongly demonstrate the competitiveness of the proposed GL-TSVM against the baseline models.
Enhancing Multiview Synergy: Robust Learning by Exploiting the Wave Loss Function with Consensus and Complementarity Principles
Aug 13, 2024Abstract:Multiview learning (MvL) is an advancing domain in machine learning, leveraging multiple data perspectives to enhance model performance through view-consistency and view-discrepancy. Despite numerous successful multiview-based SVM models, existing frameworks predominantly focus on the consensus principle, often overlooking the complementarity principle. Furthermore, they exhibit limited robustness against noisy, error-prone, and view-inconsistent samples, prevalent in multiview datasets. To tackle the aforementioned limitations, this paper introduces Wave-MvSVM, a novel multiview support vector machine framework leveraging the wave loss (W-loss) function, specifically designed to harness both consensus and complementarity principles. Unlike traditional approaches that often overlook the complementary information among different views, the proposed Wave-MvSVM ensures a more comprehensive and resilient learning process by integrating both principles effectively. The W-loss function, characterized by its smoothness, asymmetry, and bounded nature, is particularly effective in mitigating the adverse effects of noisy and outlier data, thereby enhancing model stability. Theoretically, the W-loss function also exhibits a crucial classification-calibrated property, further boosting its effectiveness. Wave-MvSVM employs a between-view co-regularization term to enforce view consistency and utilizes an adaptive combination weight strategy to maximize the discriminative power of each view. The optimization problem is efficiently solved using a combination of GD and the ADMM, ensuring reliable convergence to optimal solutions. Theoretical analyses, grounded in Rademacher complexity, validate the generalization capabilities of the Wave-MvSVM model. Extensive empirical evaluations across diverse datasets demonstrate the superior performance of Wave-MvSVM in comparison to existing benchmark models.
Advancing Supervised Learning with the Wave Loss Function: A Robust and Smooth Approach
Apr 28, 2024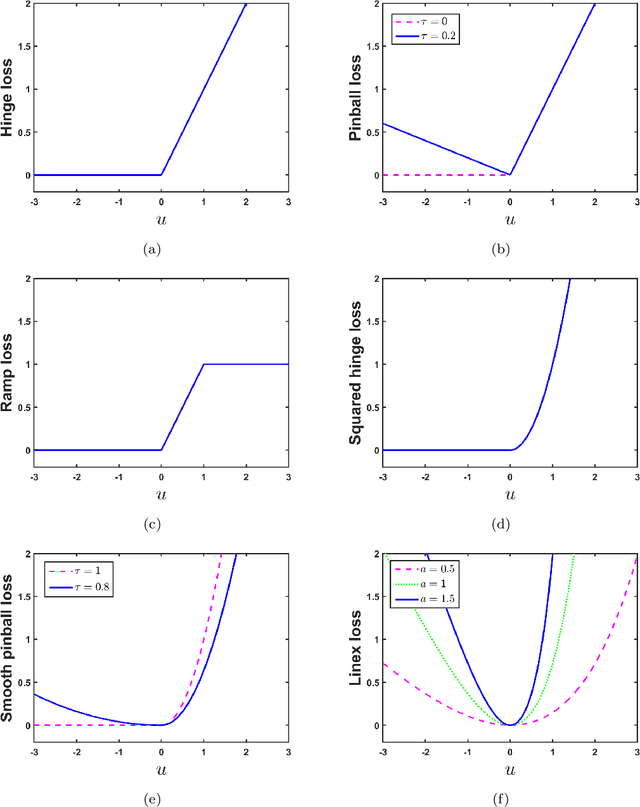

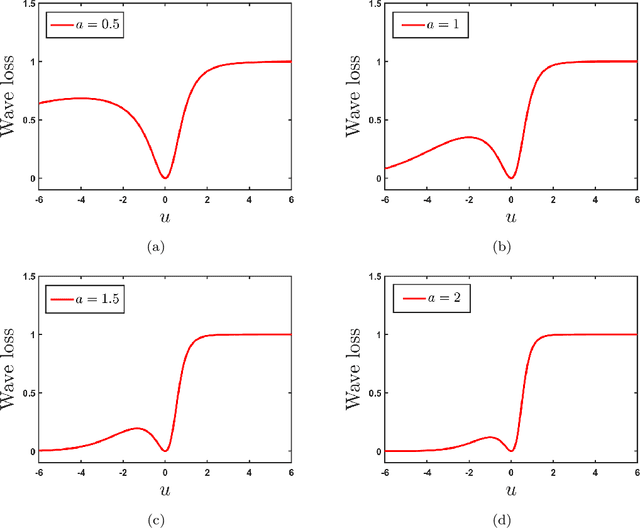

Abstract:Loss function plays a vital role in supervised learning frameworks. The selection of the appropriate loss function holds the potential to have a substantial impact on the proficiency attained by the acquired model. The training of supervised learning algorithms inherently adheres to predetermined loss functions during the optimization process. In this paper, we present a novel contribution to the realm of supervised machine learning: an asymmetric loss function named wave loss. It exhibits robustness against outliers, insensitivity to noise, boundedness, and a crucial smoothness property. Theoretically, we establish that the proposed wave loss function manifests the essential characteristic of being classification-calibrated. Leveraging this breakthrough, we incorporate the proposed wave loss function into the least squares setting of support vector machines (SVM) and twin support vector machines (TSVM), resulting in two robust and smooth models termed Wave-SVM and Wave-TSVM, respectively. To address the optimization problem inherent in Wave-SVM, we utilize the adaptive moment estimation (Adam) algorithm. It is noteworthy that this paper marks the first instance of the Adam algorithm application to solve an SVM model. Further, we devise an iterative algorithm to solve the optimization problems of Wave-TSVM. To empirically showcase the effectiveness of the proposed Wave-SVM and Wave-TSVM, we evaluate them on benchmark UCI and KEEL datasets (with and without feature noise) from diverse domains. Moreover, to exemplify the applicability of Wave-SVM in the biomedical domain, we evaluate it on the Alzheimer Disease Neuroimaging Initiative (ADNI) dataset. The experimental outcomes unequivocally reveal the prowess of Wave-SVM and Wave-TSVM in achieving superior prediction accuracy against the baseline models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge