R^2VFL: A Robust Random Vector Functional Link Network with Huber-Weighted Framework

The random vector functional link (RVFL) neural network has shown significant potential in overcoming the constraints of traditional artificial neural networks, such as excessive computation time and suboptimal solutions. However, RVFL faces challenges when dealing with noise and outliers, as it assumes all data samples contribute equally. To address this issue, we propose a novel robust framework, R2VFL, RVFL with Huber weighting function and class probability, which enhances the model's robustness and adaptability by effectively mitigating the impact of noise and outliers in the training data. The Huber weighting function reduces the influence of outliers, while the class probability mechanism assigns less weight to noisy data points, resulting in a more resilient model. We explore two distinct approaches for calculating class centers within the R2VFL framework: the simple average of all data points in each class and the median of each feature, the later providing a robust alternative by minimizing the effect of extreme values. These approaches give rise to two novel variants of the model-R2VFL-A and R2VFL-M. We extensively evaluate the proposed models on 47 UCI datasets, encompassing both binary and multiclass datasets, and conduct rigorous statistical testing, which confirms the superiority of the proposed models. Notably, the models also demonstrate exceptional performance in classifying EEG signals, highlighting their practical applicability in real-world biomedical domain.

TSVR+: Twin support vector regression with privileged information

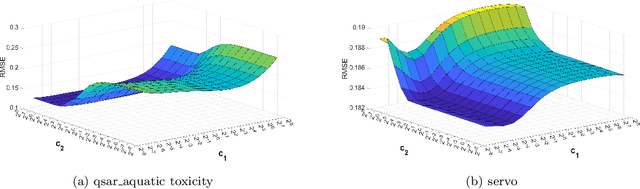
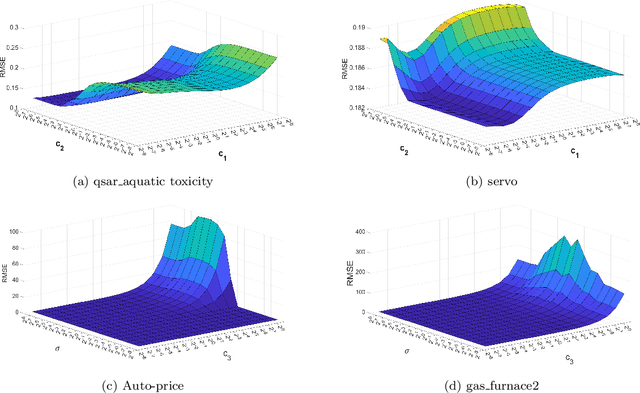
In the realm of machine learning, the data may contain additional attributes, known as privileged information (PI). The main purpose of PI is to assist in the training of the model and then utilize the acquired knowledge to make predictions for unseen samples. Support vector regression (SVR) is an effective regression model, however, it has a low learning speed due to solving a convex quadratic problem (QP) subject to a pair of constraints. In contrast, twin support vector regression (TSVR) is more efficient than SVR as it solves two QPs each subject to one set of constraints. However, TSVR and its variants are trained only on regular features and do not use privileged features for training. To fill this gap, we introduce a fusion of TSVR with learning using privileged information (LUPI) and propose a novel approach called twin support vector regression with privileged information (TSVR+). The regularization terms in the proposed TSVR+ capture the essence of statistical learning theory and implement the structural risk minimization principle. We use the successive overrelaxation (SOR) technique to solve the optimization problem of the proposed TSVR+, which enhances the training efficiency. As far as our knowledge extends, the integration of the LUPI concept into twin variants of regression models is a novel advancement. The numerical experiments conducted on UCI, stock and time series data collectively demonstrate the superiority of the proposed model.

Support matrix machine: A review

Support vector machine (SVM) is one of the most studied paradigms in the realm of machine learning for classification and regression problems. It relies on vectorized input data. However, a significant portion of the real-world data exists in matrix format, which is given as input to SVM by reshaping the matrices into vectors. The process of reshaping disrupts the spatial correlations inherent in the matrix data. Also, converting matrices into vectors results in input data with a high dimensionality, which introduces significant computational complexity. To overcome these issues in classifying matrix input data, support matrix machine (SMM) is proposed. It represents one of the emerging methodologies tailored for handling matrix input data. The SMM method preserves the structural information of the matrix data by using the spectral elastic net property which is a combination of the nuclear norm and Frobenius norm. This article provides the first in-depth analysis of the development of the SMM model, which can be used as a thorough summary by both novices and experts. We discuss numerous SMM variants, such as robust, sparse, class imbalance, and multi-class classification models. We also analyze the applications of the SMM model and conclude the article by outlining potential future research avenues and possibilities that may motivate academics to advance the SMM algorithm.