Advancing Supervised Learning with the Wave Loss Function: A Robust and Smooth Approach
Paper and Code
Apr 28, 2024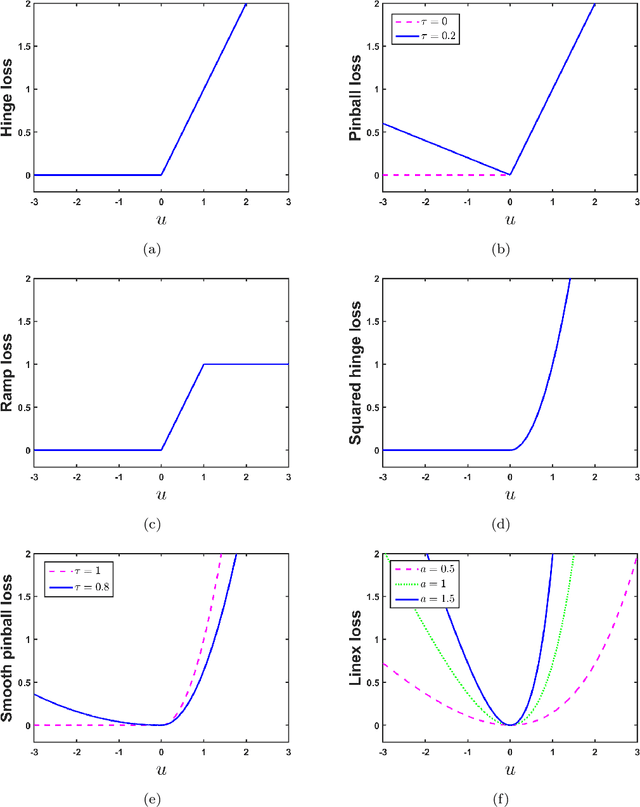

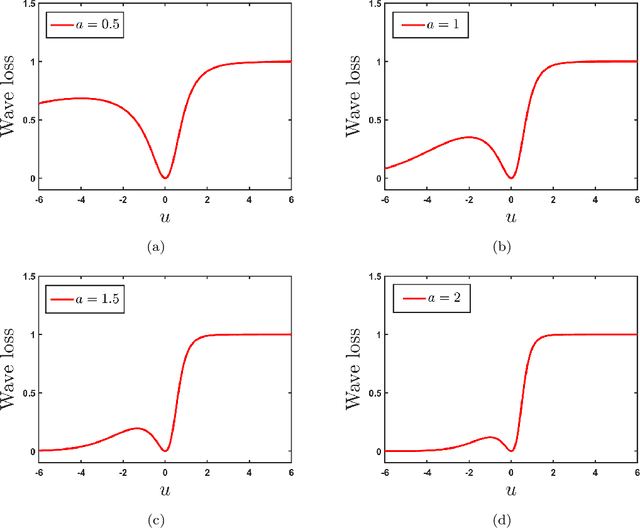

Loss function plays a vital role in supervised learning frameworks. The selection of the appropriate loss function holds the potential to have a substantial impact on the proficiency attained by the acquired model. The training of supervised learning algorithms inherently adheres to predetermined loss functions during the optimization process. In this paper, we present a novel contribution to the realm of supervised machine learning: an asymmetric loss function named wave loss. It exhibits robustness against outliers, insensitivity to noise, boundedness, and a crucial smoothness property. Theoretically, we establish that the proposed wave loss function manifests the essential characteristic of being classification-calibrated. Leveraging this breakthrough, we incorporate the proposed wave loss function into the least squares setting of support vector machines (SVM) and twin support vector machines (TSVM), resulting in two robust and smooth models termed Wave-SVM and Wave-TSVM, respectively. To address the optimization problem inherent in Wave-SVM, we utilize the adaptive moment estimation (Adam) algorithm. It is noteworthy that this paper marks the first instance of the Adam algorithm application to solve an SVM model. Further, we devise an iterative algorithm to solve the optimization problems of Wave-TSVM. To empirically showcase the effectiveness of the proposed Wave-SVM and Wave-TSVM, we evaluate them on benchmark UCI and KEEL datasets (with and without feature noise) from diverse domains. Moreover, to exemplify the applicability of Wave-SVM in the biomedical domain, we evaluate it on the Alzheimer Disease Neuroimaging Initiative (ADNI) dataset. The experimental outcomes unequivocally reveal the prowess of Wave-SVM and Wave-TSVM in achieving superior prediction accuracy against the baseline models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge