Advancing RVFL networks: Robust classification with the HawkEye loss function

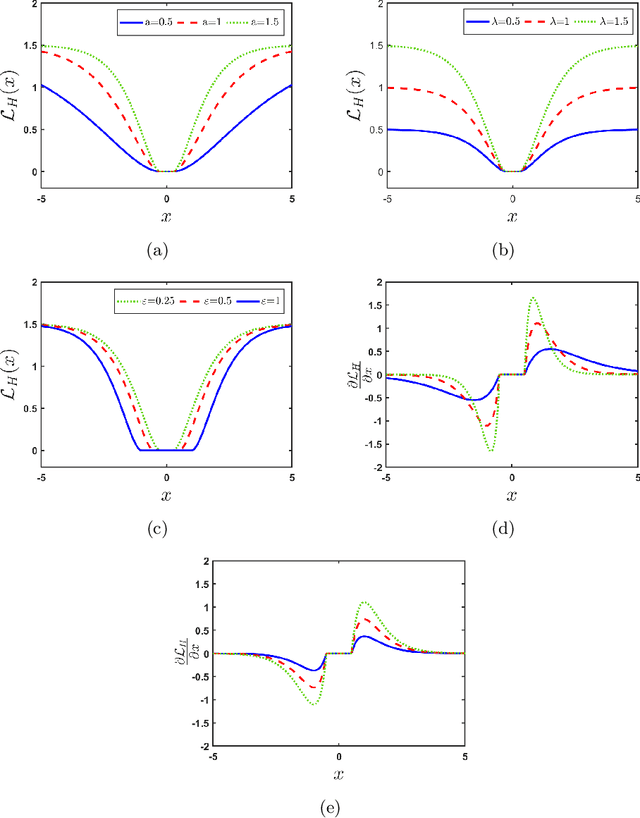
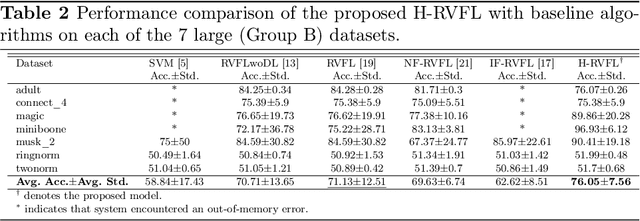
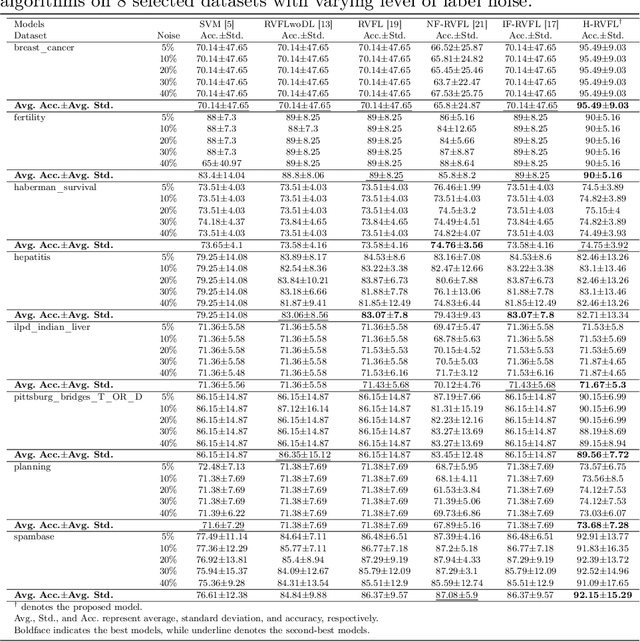
Random vector functional link (RVFL), a variant of single-layer feedforward neural network (SLFN), has garnered significant attention due to its lower computational cost and robustness to overfitting. Despite its advantages, the RVFL network's reliance on the square error loss function makes it highly sensitive to outliers and noise, leading to degraded model performance in real-world applications. To remedy it, we propose the incorporation of the HawkEye loss (H-loss) function into the RVFL framework. The H-loss function features nice mathematical properties, including smoothness and boundedness, while simultaneously incorporating an insensitive zone. Each characteristic brings its own advantages: 1) Boundedness limits the impact of extreme errors, enhancing robustness against outliers; 2) Smoothness facilitates the use of gradient-based optimization algorithms, ensuring stable and efficient convergence; and 3) The insensitive zone mitigates the effect of minor discrepancies and noise. Leveraging the H-loss function, we embed it into the RVFL framework and develop a novel robust RVFL model termed H-RVFL. Notably, this work addresses a significant gap, as no bounded loss function has been incorporated into RVFL to date. The non-convex optimization of the proposed H-RVFL is effectively addressed by the Nesterov accelerated gradient (NAG) algorithm, whose computational complexity is also discussed. The proposed H-RVFL model's effectiveness is validated through extensive experiments on $40$ benchmark datasets from UCI and KEEL repositories, with and without label noise. The results highlight significant improvements in robustness and efficiency, establishing the H-RVFL model as a powerful tool for applications in noisy and outlier-prone environments.