Decision Theory-Guided Deep Reinforcement Learning for Fast Learning

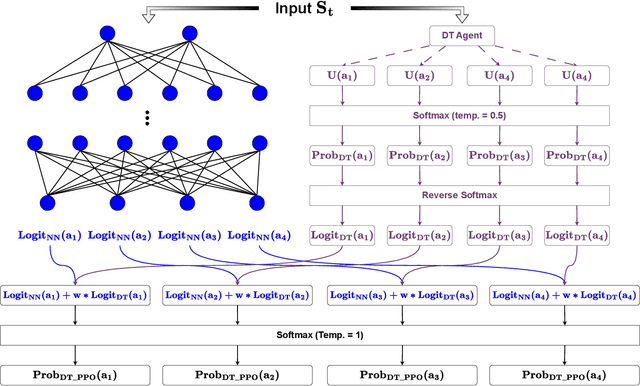
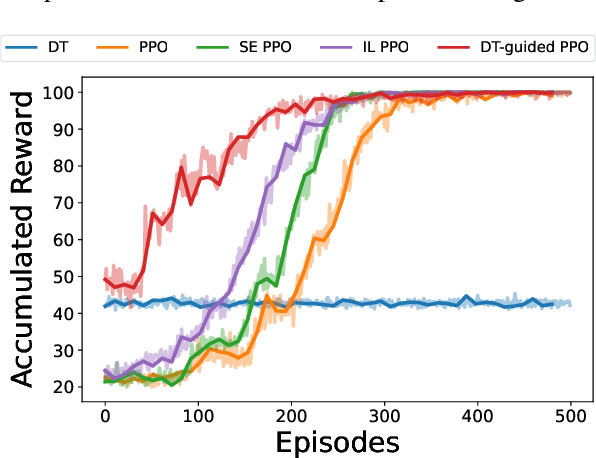
This paper introduces a novel approach, Decision Theory-guided Deep Reinforcement Learning (DT-guided DRL), to address the inherent cold start problem in DRL. By integrating decision theory principles, DT-guided DRL enhances agents' initial performance and robustness in complex environments, enabling more efficient and reliable convergence during learning. Our investigation encompasses two primary problem contexts: the cart pole and maze navigation challenges. Experimental results demonstrate that the integration of decision theory not only facilitates effective initial guidance for DRL agents but also promotes a more structured and informed exploration strategy, particularly in environments characterized by large and intricate state spaces. The results of experiment demonstrate that DT-guided DRL can provide significantly higher rewards compared to regular DRL. Specifically, during the initial phase of training, the DT-guided DRL yields up to an 184% increase in accumulated reward. Moreover, even after reaching convergence, it maintains a superior performance, ending with up to 53% more reward than standard DRL in large maze problems. DT-guided DRL represents an advancement in mitigating a fundamental challenge of DRL by leveraging functions informed by human (designer) knowledge, setting a foundation for further research in this promising interdisciplinary domain.

Restricted Tweedie Stochastic Block Models

The stochastic block model (SBM) is a widely used framework for community detection in networks, where the network structure is typically represented by an adjacency matrix. However, conventional SBMs are not directly applicable to an adjacency matrix that consists of non-negative zero-inflated continuous edge weights. To model the international trading network, where edge weights represent trading values between countries, we propose an innovative SBM based on a restricted Tweedie distribution. Additionally, we incorporate nodal information, such as the geographical distance between countries, and account for its dynamic effect on edge weights. Notably, we show that given a sufficiently large number of nodes, estimating this covariate effect becomes independent of community labels of each node when computing the maximum likelihood estimator of parameters in our model. This result enables the development of an efficient two-step algorithm that separates the estimation of covariate effects from other parameters. We demonstrate the effectiveness of our proposed method through extensive simulation studies and an application to real-world international trading data.

Dependence model assessment and selection with DecoupleNets

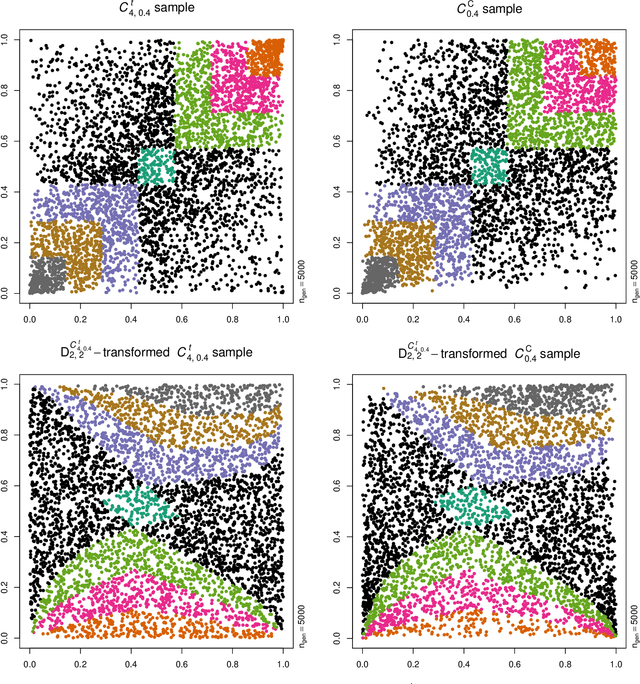
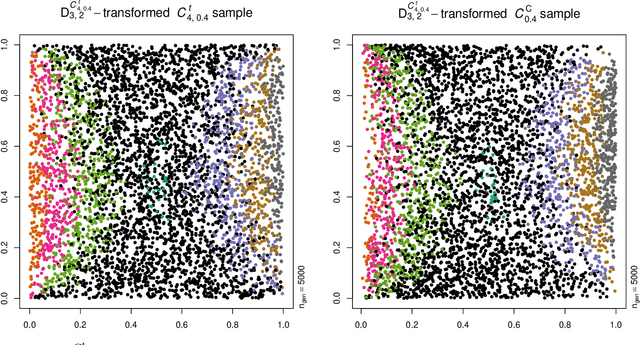
Neural networks are suggested for learning a map from $d$-dimensional samples with any underlying dependence structure to multivariate uniformity in $d'$ dimensions. This map, termed DecoupleNet, is used for dependence model assessment and selection. If the data-generating dependence model was known, and if it was among the few analytically tractable ones, one such transformation for $d'=d$ is Rosenblatt's transform. DecoupleNets only require an available sample and are applicable to $d'<d$, in particular $d'=2$. This allows for simpler model assessment and selection without loss of information, both numerically and, because $d'=2$, graphically. Through simulation studies based on data from various copulas, the feasibility and validity of this novel approach is demonstrated. Applications to real world data illustrate its usefulness for model assessment and selection.

RafterNet: Probabilistic predictions in multi-response regression

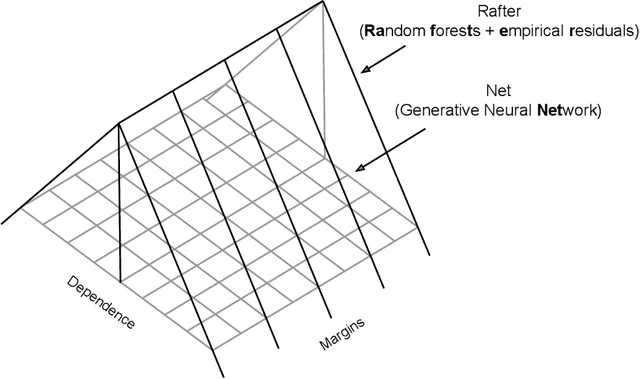
A fully nonparametric approach for making probabilistic predictions in multi-response regression problems is introduced. Random forests are used as marginal models for each response variable and, as novel contribution of the present work, the dependence between the multiple response variables is modeled by a generative neural network. This combined modeling approach of random forests, corresponding empirical marginal residual distributions and a generative neural network is referred to as RafterNet. Multiple datasets serve as examples to demonstrate the flexibility of the approach and its impact for making probabilistic forecasts.

Game-Theoretic and Machine Learning-based Approaches for Defensive Deception: A Survey

Defensive deception is a promising approach for cyberdefense. Although defensive deception is increasingly popular in the research community, there has not been a systematic investigation of its key components, the underlying principles, and its tradeoffs in various problem settings. This survey paper focuses on defensive deception research centered on game theory and machine learning, since these are prominent families of artificial intelligence approaches that are widely employed in defensive deception. This paper brings forth insights, lessons, and limitations from prior work. It closes with an outline of some research directions to tackle major gaps in current defensive deception research.

Applications of multivariate quasi-random sampling with neural networks

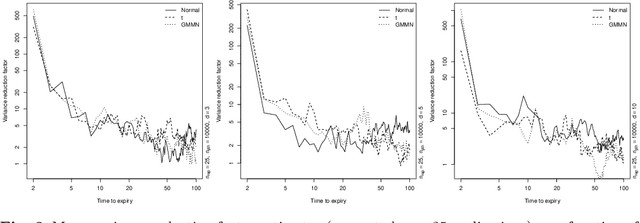
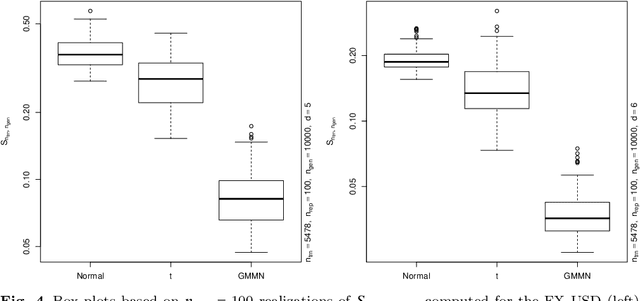
Generative moment matching networks (GMMNs) are suggested for modeling the cross-sectional dependence between stochastic processes. The stochastic processes considered are geometric Brownian motions and ARMA-GARCH models. Geometric Brownian motions lead to an application of pricing American basket call options under dependence and ARMA-GARCH models lead to an application of simulating predictive distributions. In both types of applications the benefit of using GMMNs in comparison to parametric dependence models is highlighted and the fact that GMMNs can produce dependent quasi-random samples with no additional effort is exploited to obtain variance reduction.

Multivariate time-series modeling with generative neural networks

Generative moment matching networks (GMMNs) are introduced as dependence models for the joint innovation distribution of multivariate time series (MTS). Following the popular copula-GARCH approach for modeling dependent MTS data, a framework allowing us to take an alternative GMMN-GARCH approach is presented. First, ARMA-GARCH models are utilized to capture the serial dependence within each univariate marginal time series. Second, if the number of marginal time series is large, principal component analysis (PCA) is used as a dimension-reduction step. Last, the remaining cross-sectional dependence is modeled via a GMMN, our main contribution. GMMNs are highly flexible and easy to simulate from, which is a major advantage over the copula-GARCH approach. Applications involving yield curve modeling and the analysis of foreign exchange rate returns are presented to demonstrate the utility of our approach, especially in terms of producing better empirical predictive distributions and making better probabilistic forecasts. All results are reproducible with the demo GMMN_MTS_paper of the R package gnn.

Quasi-random number generators for multivariate distributions based on generative neural networks

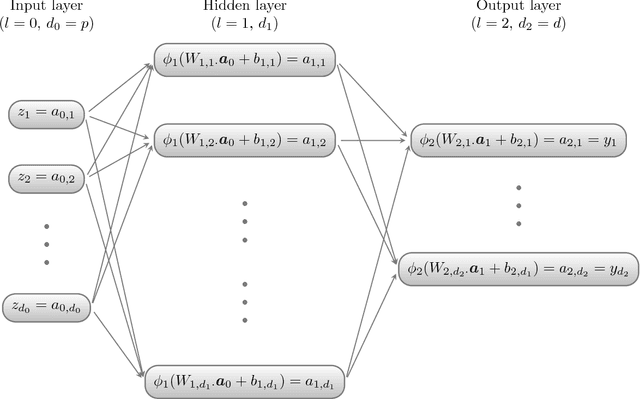
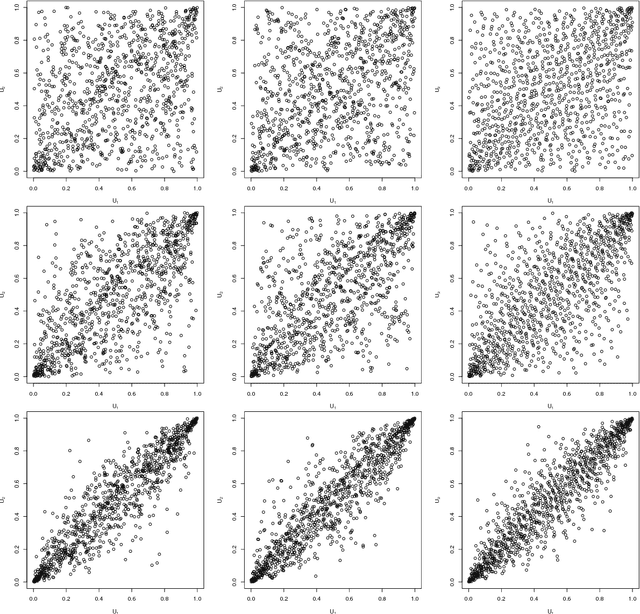
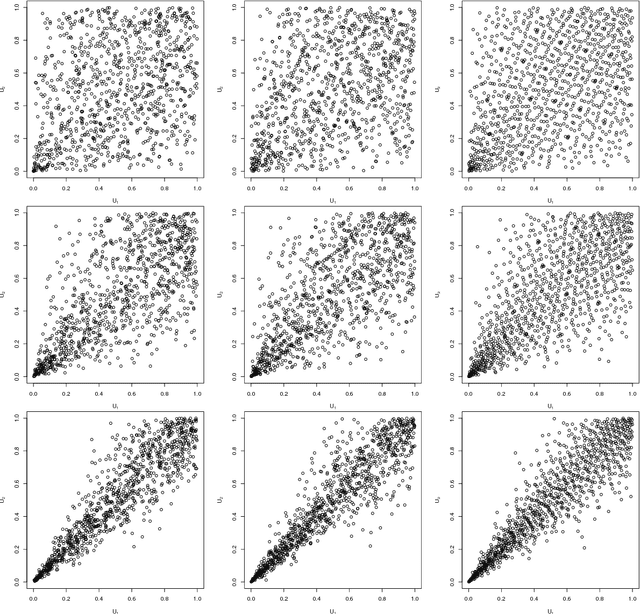
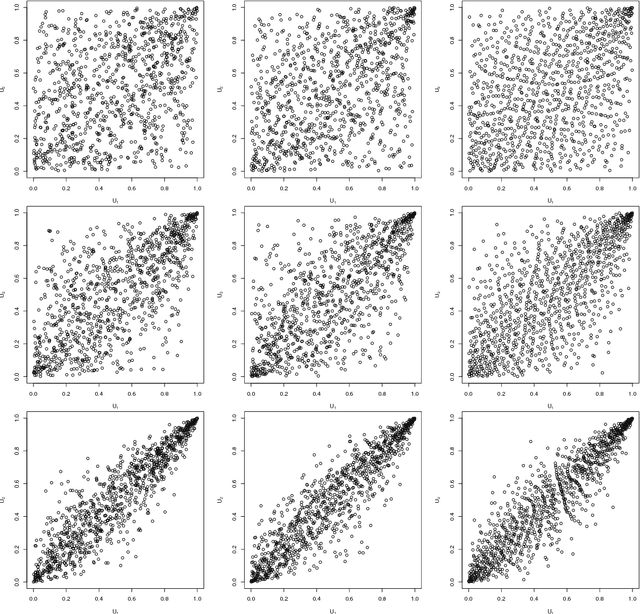
Generative moment matching networks are introduced as quasi-random number generators for multivariate distributions. So far, quasi-random number generators for non-uniform multivariate distributions require a careful design, often need to exploit specific properties of the distribution or quasi-random number sequence under consideration, and are limited to few models. Utilizing generative neural networks, in particular, generative moment matching networks, allows one to construct quasi-random number generators for a much larger variety of multivariate distributions without such restrictions. Once trained, the presented generators only require independent quasi-random numbers as input and are thus fast in generating non-uniform multivariate quasi-random number sequences from the target distribution. Various numerical examples are considered to demonstrate the approach, including applications inspired by risk management practice.

Pruning variable selection ensembles

In the context of variable selection, ensemble learning has gained increasing interest due to its great potential to improve selection accuracy and to reduce false discovery rate. A novel ordering-based selective ensemble learning strategy is designed in this paper to obtain smaller but more accurate ensembles. In particular, a greedy sorting strategy is proposed to rearrange the order by which the members are included into the integration process. Through stopping the fusion process early, a smaller subensemble with higher selection accuracy can be obtained. More importantly, the sequential inclusion criterion reveals the fundamental strength-diversity trade-off among ensemble members. By taking stability selection (abbreviated as StabSel) as an example, some experiments are conducted with both simulated and real-world data to examine the performance of the novel algorithm. Experimental results demonstrate that pruned StabSel generally achieves higher selection accuracy and lower false discovery rates than StabSel and several other benchmark methods.

Expanded Alternating Optimization of Nonconvex Functions with Applications to Matrix Factorization and Penalized Regression

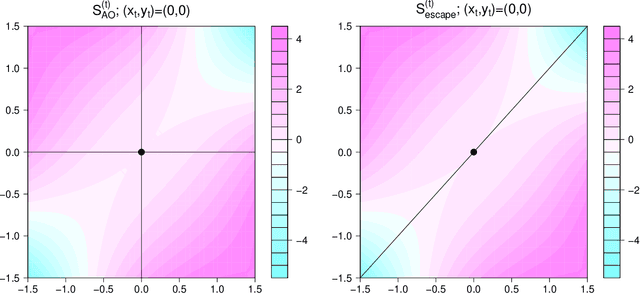
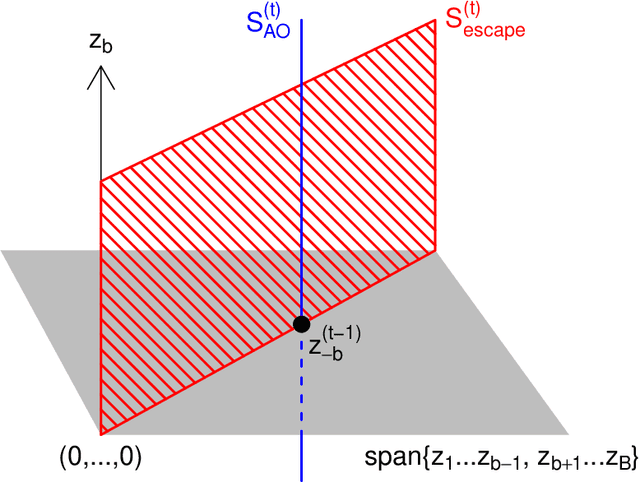
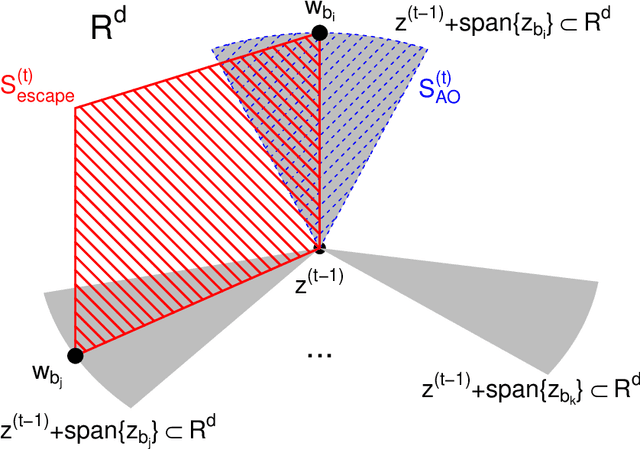
We propose a general technique for improving alternating optimization (AO) of nonconvex functions. Starting from the solution given by AO, we conduct another sequence of searches over subspaces that are both meaningful to the optimization problem at hand and different from those used by AO. To demonstrate the utility of our approach, we apply it to the matrix factorization (MF) algorithm for recommender systems and the coordinate descent algorithm for penalized regression (PR), and show meaningful improvements using both real-world (for MF) and simulated (for PR) data sets. Moreover, we demonstrate for MF that, by constructing search spaces customized to the given data set, we can significantly increase the convergence rate of our technique.