Expanded Alternating Optimization of Nonconvex Functions with Applications to Matrix Factorization and Penalized Regression
Paper and Code
Dec 12, 2014

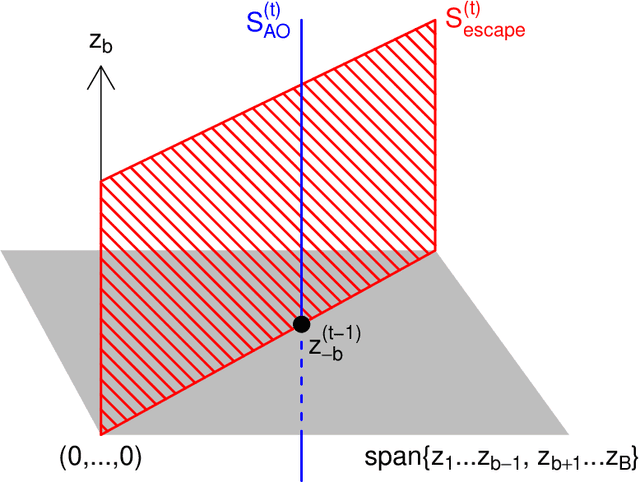
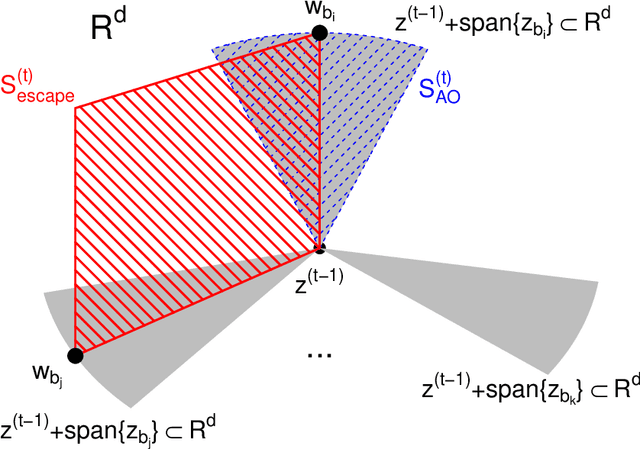
We propose a general technique for improving alternating optimization (AO) of nonconvex functions. Starting from the solution given by AO, we conduct another sequence of searches over subspaces that are both meaningful to the optimization problem at hand and different from those used by AO. To demonstrate the utility of our approach, we apply it to the matrix factorization (MF) algorithm for recommender systems and the coordinate descent algorithm for penalized regression (PR), and show meaningful improvements using both real-world (for MF) and simulated (for PR) data sets. Moreover, we demonstrate for MF that, by constructing search spaces customized to the given data set, we can significantly increase the convergence rate of our technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge