Dependence model assessment and selection with DecoupleNets
Paper and Code
Feb 07, 2022
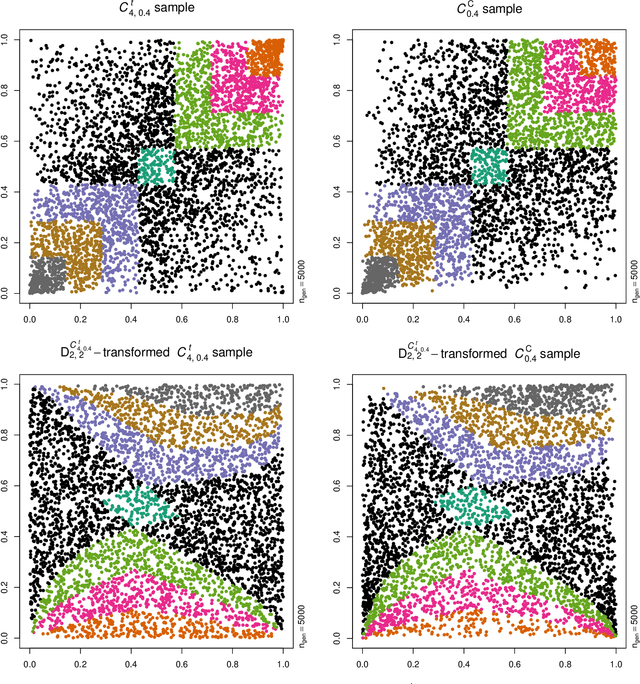
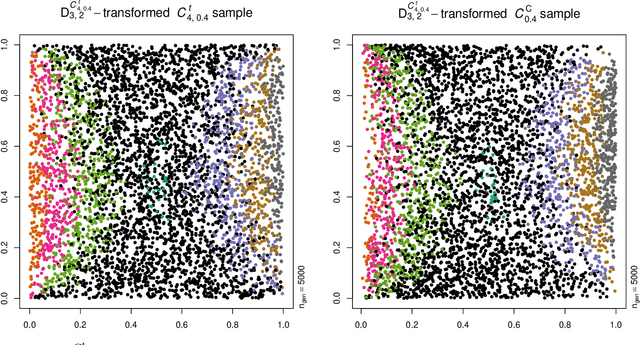

Neural networks are suggested for learning a map from $d$-dimensional samples with any underlying dependence structure to multivariate uniformity in $d'$ dimensions. This map, termed DecoupleNet, is used for dependence model assessment and selection. If the data-generating dependence model was known, and if it was among the few analytically tractable ones, one such transformation for $d'=d$ is Rosenblatt's transform. DecoupleNets only require an available sample and are applicable to $d'<d$, in particular $d'=2$. This allows for simpler model assessment and selection without loss of information, both numerically and, because $d'=2$, graphically. Through simulation studies based on data from various copulas, the feasibility and validity of this novel approach is demonstrated. Applications to real world data illustrate its usefulness for model assessment and selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge