Olaf: Bringing an Animated Character to Life in the Physical World

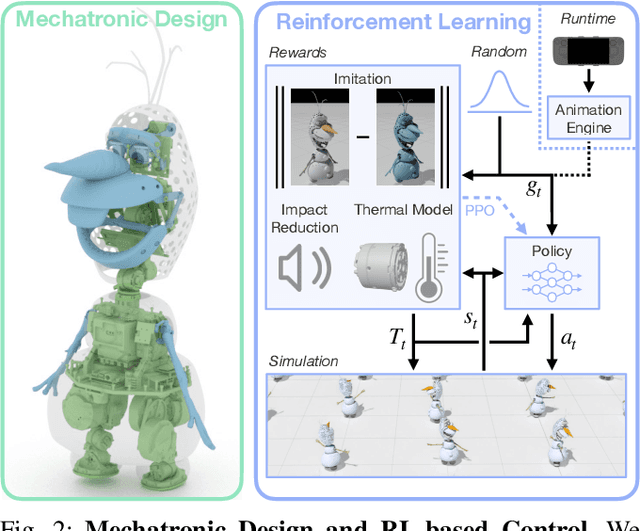
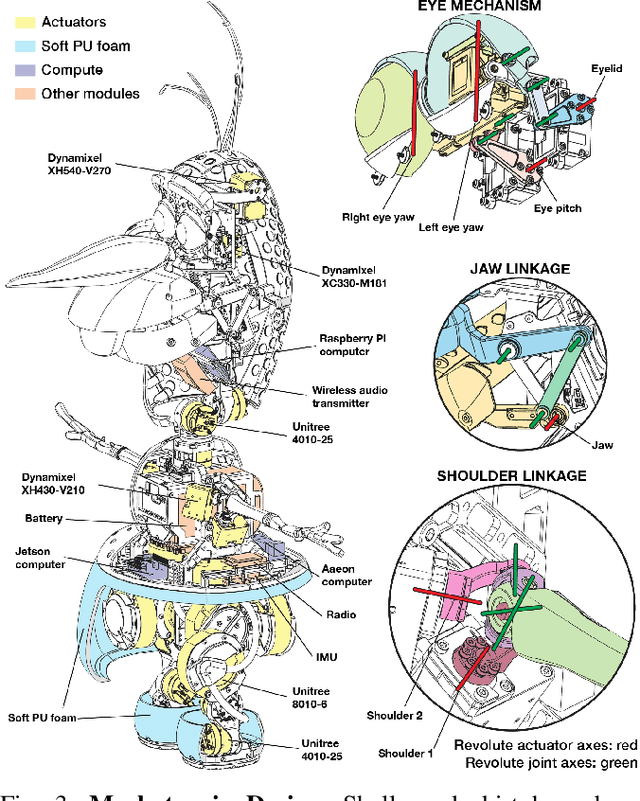
Animated characters often move in non-physical ways and have proportions that are far from a typical walking robot. This provides an ideal platform for innovation in both mechanical design and stylized motion control. In this paper, we bring Olaf to life in the physical world, relying on reinforcement learning guided by animation references for control. To create the illusion of Olaf's feet moving along his body, we hide two asymmetric legs under a soft foam skirt. To fit actuators inside the character, we use spherical and planar linkages in the arms, mouth, and eyes. Because the walk cycle results in harsh contact sounds, we introduce additional rewards that noticeably reduce impact noise. The large head, driven by small actuators in the character's slim neck, creates a risk of overheating, amplified by the costume. To keep actuators from overheating, we feed temperature values as additional inputs to policies, introducing new rewards to keep them within bounds. We validate the efficacy of our modeling in simulation and on hardware, demonstrating an unmatched level of believability for a costumed robotic character.

Robot Crash Course: Learning Soft and Stylized Falling

Despite recent advances in robust locomotion, bipedal robots operating in the real world remain at risk of falling. While most research focuses on preventing such events, we instead concentrate on the phenomenon of falling itself. Specifically, we aim to reduce physical damage to the robot while providing users with control over a robot's end pose. To this end, we propose a robot agnostic reward function that balances the achievement of a desired end pose with impact minimization and the protection of critical robot parts during reinforcement learning. To make the policy robust to a broad range of initial falling conditions and to enable the specification of an arbitrary and unseen end pose at inference time, we introduce a simulation-based sampling strategy of initial and end poses. Through simulated and real-world experiments, our work demonstrates that even bipedal robots can perform controlled, soft falls.

AMOR: Adaptive Character Control through Multi-Objective Reinforcement Learning

Reinforcement learning (RL) has significantly advanced the control of physics-based and robotic characters that track kinematic reference motion. However, methods typically rely on a weighted sum of conflicting reward functions, requiring extensive tuning to achieve a desired behavior. Due to the computational cost of RL, this iterative process is a tedious, time-intensive task. Furthermore, for robotics applications, the weights need to be chosen such that the policy performs well in the real world, despite inevitable sim-to-real gaps. To address these challenges, we propose a multi-objective reinforcement learning framework that trains a single policy conditioned on a set of weights, spanning the Pareto front of reward trade-offs. Within this framework, weights can be selected and tuned after training, significantly speeding up iteration time. We demonstrate how this improved workflow can be used to perform highly dynamic motions with a robot character. Moreover, we explore how weight-conditioned policies can be leveraged in hierarchical settings, using a high-level policy to dynamically select weights according to the current task. We show that the multi-objective policy encodes a diverse spectrum of behaviors, facilitating efficient adaptation to novel tasks.

On Solving the Dynamics of Constrained Rigid Multi-Body Systems with Kinematic Loops

This technical report provides an in-depth evaluation of both established and state-of-the-art methods for simulating constrained rigid multi-body systems with hard-contact dynamics, using formulations of Nonlinear Complementarity Problems (NCPs). We are particularly interest in examining the simulation of highly coupled mechanical systems with multitudes of closed-loop bilateral kinematic joint constraints in the presence of additional unilateral constraints such as joint limits and frictional contacts with restitutive impacts. This work thus presents an up-to-date literature survey of the relevant fields, as well as an in-depth description of the approaches used for the formulation and solving of the numerical time-integration problem in a maximal coordinate setting. More specifically, our focus lies on a version of the overall problem that decomposes it into the forward dynamics problem followed by a time-integration using the states of the bodies and the constraint reactions rendered by the former. We then proceed to elaborate on the formulations used to model frictional contact dynamics and define a set of solvers that are representative of those currently employed in the majority of the established physics engines. A key aspect of this work is the definition of a benchmarking framework that we propose as a means to both qualitatively and quantitatively evaluate the performance envelopes of the set of solvers on a diverse set of challenging simulation scenarios. We thus present an extensive set of experiments that aim at highlighting the absolute and relative performance of all solvers on particular problems of interest as well as aggravatingly over the complete set defined in the suite.

Spline-based Transformers

We introduce Spline-based Transformers, a novel class of Transformer models that eliminate the need for positional encoding. Inspired by workflows using splines in computer animation, our Spline-based Transformers embed an input sequence of elements as a smooth trajectory in latent space. Overcoming drawbacks of positional encoding such as sequence length extrapolation, Spline-based Transformers also provide a novel way for users to interact with transformer latent spaces by directly manipulating the latent control points to create new latent trajectories and sequences. We demonstrate the superior performance of our approach in comparison to conventional positional encoding on a variety of datasets, ranging from synthetic 2D to large-scale real-world datasets of images, 3D shapes, and animations.

Autonomous Human-Robot Interaction via Operator Imitation

Teleoperated robotic characters can perform expressive interactions with humans, relying on the operators' experience and social intuition. In this work, we propose to create autonomous interactive robots, by training a model to imitate operator data. Our model is trained on a dataset of human-robot interactions, where an expert operator is asked to vary the interactions and mood of the robot, while the operator commands as well as the pose of the human and robot are recorded. Our approach learns to predict continuous operator commands through a diffusion process and discrete commands through a classifier, all unified within a single transformer architecture. We evaluate the resulting model in simulation and with a user study on the real system. We show that our method enables simple autonomous human-robot interactions that are comparable to the expert-operator baseline, and that users can recognize the different robot moods as generated by our model. Finally, we demonstrate a zero-shot transfer of our model onto a different robotic platform with the same operator interface.

Design and Control of a Bipedal Robotic Character

Legged robots have achieved impressive feats in dynamic locomotion in challenging unstructured terrain. However, in entertainment applications, the design and control of these robots face additional challenges in appealing to human audiences. This work aims to unify expressive, artist-directed motions and robust dynamic mobility for legged robots. To this end, we introduce a new bipedal robot, designed with a focus on character-driven mechanical features. We present a reinforcement learning-based control architecture to robustly execute artistic motions conditioned on command signals. During runtime, these command signals are generated by an animation engine which composes and blends between multiple animation sources. Finally, an intuitive operator interface enables real-time show performances with the robot. The complete system results in a believable robotic character, and paves the way for enhanced human-robot engagement in various contexts, in entertainment robotics and beyond.

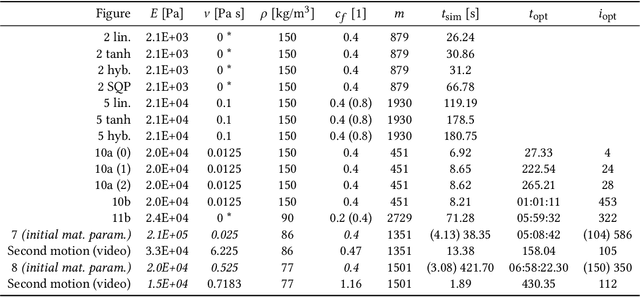
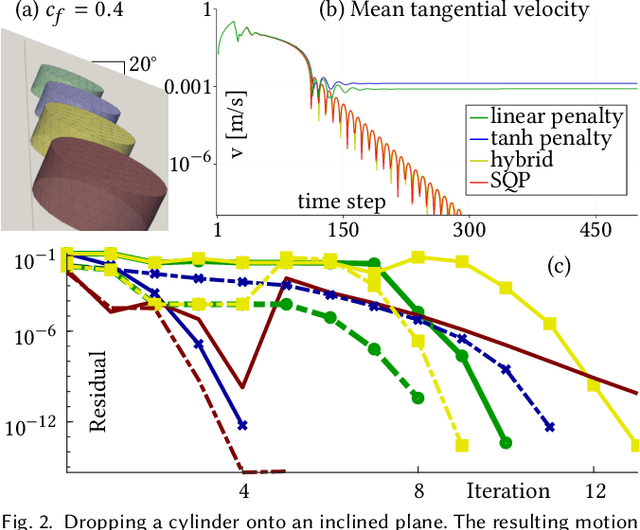
ADD: Analytically Differentiable Dynamics for Multi-Body Systems with Frictional Contact

We present a differentiable dynamics solver that is able to handle frictional contact for rigid and deformable objects within a unified framework. Through a principled mollification of normal and tangential contact forces, our method circumvents the main difficulties inherent to the non-smooth nature of frictional contact. We combine this new contact model with fully-implicit time integration to obtain a robust and efficient dynamics solver that is analytically differentiable. In conjunction with adjoint sensitivity analysis, our formulation enables gradient-based optimization with adaptive trade-offs between simulation accuracy and smoothness of objective function landscapes. We thoroughly analyse our approach on a set of simulation examples involving rigid bodies, visco-elastic materials, and coupled multi-body systems. We furthermore showcase applications of our differentiable simulator to parameter estimation for deformable objects, motion planning for robotic manipulation, trajectory optimization for compliant walking robots, as well as efficient self-supervised learning of control policies.