Changes from Classical Statistics to Modern Statistics and Data Science

A coordinate system is a foundation for every quantitative science, engineering, and medicine. Classical physics and statistics are based on the Cartesian coordinate system. The classical probability and hypothesis testing theory can only be applied to Euclidean data. However, modern data in the real world are from natural language processing, mathematical formulas, social networks, transportation and sensor networks, computer visions, automations, and biomedical measurements. The Euclidean assumption is not appropriate for non Euclidean data. This perspective addresses the urgent need to overcome those fundamental limitations and encourages extensions of classical probability theory and hypothesis testing , diffusion models and stochastic differential equations from Euclidean space to non Euclidean space. Artificial intelligence such as natural language processing, computer vision, graphical neural networks, manifold regression and inference theory, manifold learning, graph neural networks, compositional diffusion models for automatically compositional generations of concepts and demystifying machine learning systems, has been rapidly developed. Differential manifold theory is the mathematic foundations of deep learning and data science as well. We urgently need to shift the paradigm for data analysis from the classical Euclidean data analysis to both Euclidean and non Euclidean data analysis and develop more and more innovative methods for describing, estimating and inferring non Euclidean geometries of modern real datasets. A general framework for integrated analysis of both Euclidean and non Euclidean data, composite AI, decision intelligence and edge AI provide powerful innovative ideas and strategies for fundamentally advancing AI. We are expected to marry statistics with AI, develop a unified theory of modern statistics and drive next generation of AI and data science.

A New Statistical Framework for Genetic Pleiotropic Analysis of High Dimensional Phenotype Data

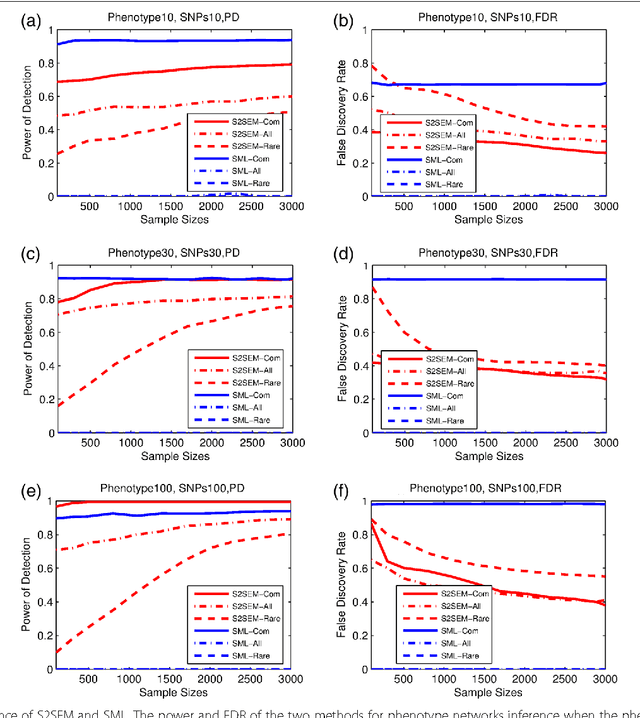
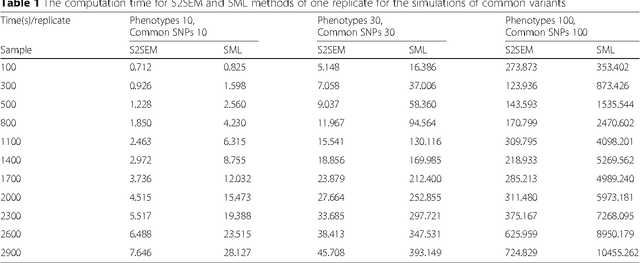
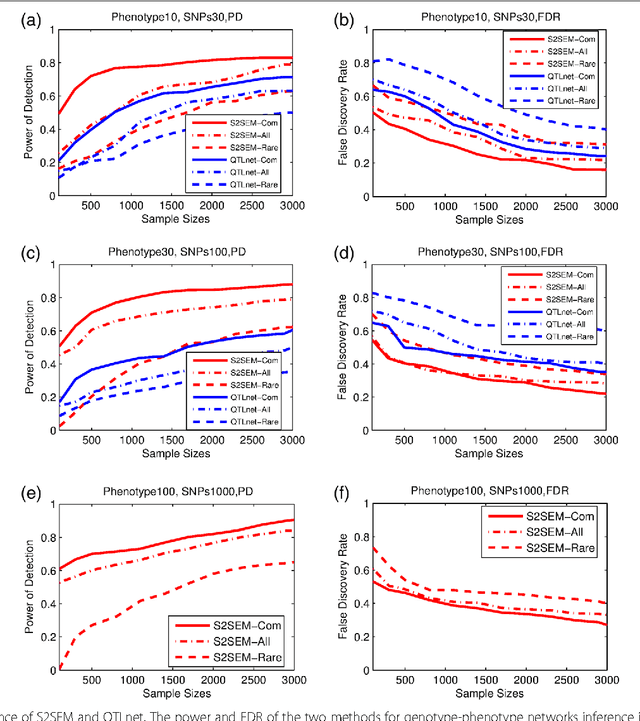
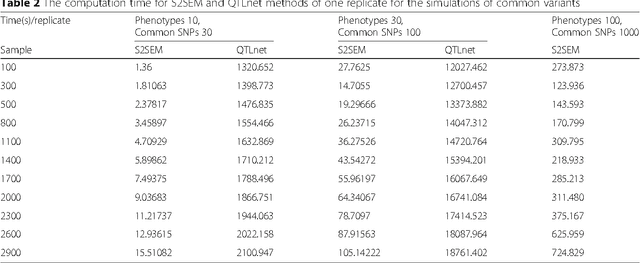
The widely used genetic pleiotropic analysis of multiple phenotypes are often designed for examining the relationship between common variants and a few phenotypes. They are not suited for both high dimensional phenotypes and high dimensional genotype (next-generation sequencing) data. To overcome these limitations, we develop sparse structural equation models (SEMs) as a general framework for a new paradigm of genetic analysis of multiple phenotypes. To incorporate both common and rare variants into the analysis, we extend the traditional multivariate SEMs to sparse functional SEMs. To deal with high dimensional phenotype and genotype data, we employ functional data analysis and the alternative direction methods of multiplier (ADMM) techniques to reduce data dimension and improve computational efficiency. Using large scale simulations we showed that the proposed methods have higher power to detect true causal genetic pleiotropic structure than other existing methods. Simulations also demonstrate that the gene-based pleiotropic analysis has higher power than the single variant-based pleiotropic analysis. The proposed method is applied to exome sequence data from the NHLBI Exome Sequencing Project (ESP) with 11 phenotypes, which identifies a network with 137 genes connected to 11 phenotypes and 341 edges. Among them, 114 genes showed pleiotropic genetic effects and 45 genes were reported to be associated with phenotypes in the analysis or other cardiovascular disease (CVD) related phenotypes in the literature.

Random Bits Regression: a Strong General Predictor for Big Data

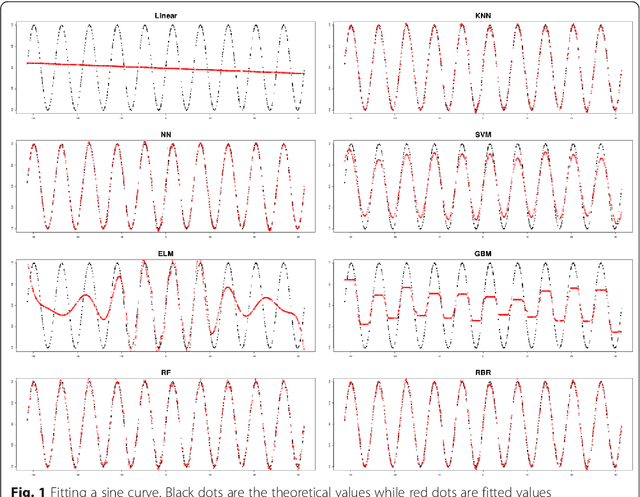
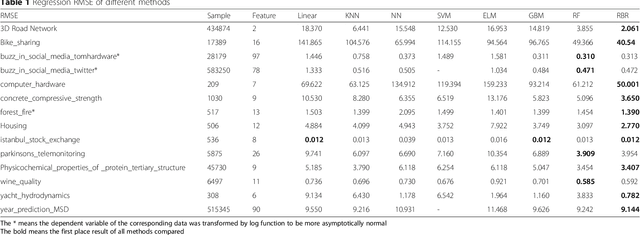
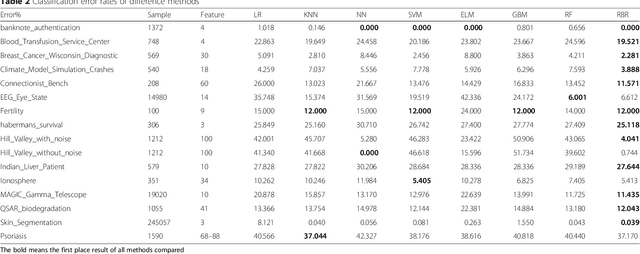
To improve accuracy and speed of regressions and classifications, we present a data-based prediction method, Random Bits Regression (RBR). This method first generates a large number of random binary intermediate/derived features based on the original input matrix, and then performs regularized linear/logistic regression on those intermediate/derived features to predict the outcome. Benchmark analyses on a simulated dataset, UCI machine learning repository datasets and a GWAS dataset showed that RBR outperforms other popular methods in accuracy and robustness. RBR (available on https://sourceforge.net/projects/rbr/) is very fast and requires reasonable memories, therefore, provides a strong, robust and fast predictor in the big data era.

A Novel Statistical Method Based on Dynamic Models for Classification

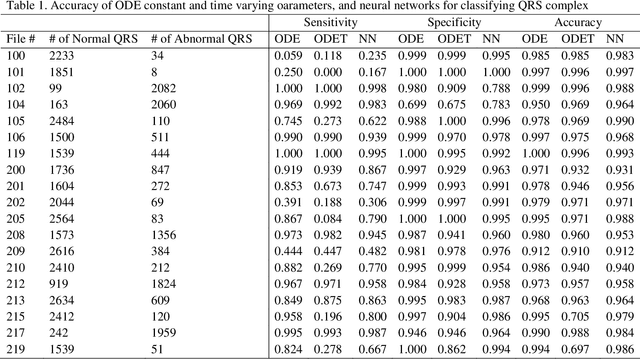
Realizations of stochastic process are often observed temporal data or functional data. There are growing interests in classification of dynamic or functional data. The basic feature of functional data is that the functional data have infinite dimensions and are highly correlated. An essential issue for classifying dynamic and functional data is how to effectively reduce their dimension and explore dynamic feature. However, few statistical methods for dynamic data classification have directly used rich dynamic features of the data. We propose to use second order ordinary differential equation (ODE) to model dynamic process and principal differential analysis to estimate constant or time-varying parameters in the ODE. We examine differential dynamic properties of the dynamic system across different conditions including stability and transient-response, which determine how the dynamic systems maintain their functions and performance under a broad range of random internal and external perturbations. We use the parameters in the ODE as features for classifiers. As a proof of principle, the proposed methods are applied to classifying normal and abnormal QRS complexes in the electrocardiogram (ECG) data analysis, which is of great clinical values in diagnosis of cardiovascular diseases. We show that the ODE-based classification methods in QRS complex classification outperform the currently widely used neural networks with Fourier expansion coefficients of the functional data as their features. We expect that the dynamic model-based classification methods may open a new avenue for functional data classification.

Fully Automated Myocardial Infarction Classification using Ordinary Differential Equations

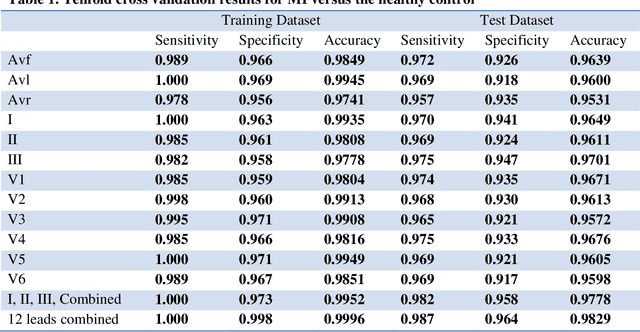
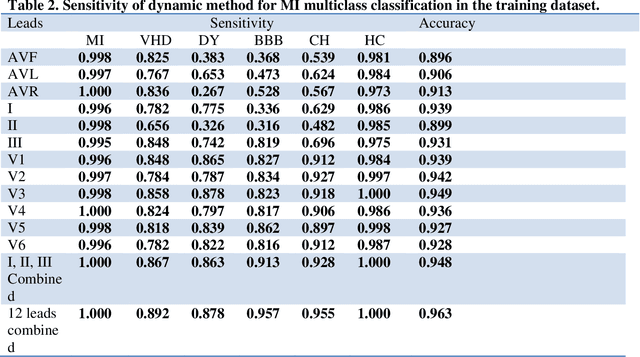
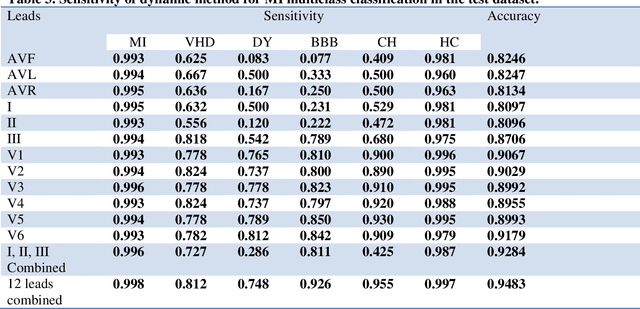
Portable, Wearable and Wireless electrocardiogram (ECG) Systems have the potential to be used as point-of-care for cardiovascular disease diagnostic systems. Such wearable and wireless ECG systems require automatic detection of cardiovascular disease. Even in the primary care, automation of ECG diagnostic systems will improve efficiency of ECG diagnosis and reduce the minimal training requirement of local healthcare workers. However, few fully automatic myocardial infarction (MI) disease detection algorithms have well been developed. This paper presents a novel automatic MI classification algorithm using second order ordinary differential equation (ODE) with time varying coefficients, which simultaneously captures morphological and dynamic feature of highly correlated ECG signals. By effectively estimating the unobserved state variables and the parameters of the second order ODE, the accuracy of the classification was significantly improved. The estimated time varying coefficients of the second order ODE were used as an input to the support vector machine (SVM) for the MI classification. The proposed method was applied to the PTB diagnostic ECG database within Physionet. The overall sensitivity, specificity, and classification accuracy of 12 lead ECGs for MI binary classifications were 98.7%, 96.4% and 98.3%, respectively. We also found that even using one lead ECG signals, we can reach accuracy as high as 97%. Multiclass MI classification is a challenging task but the developed ODE approach for 12 lead ECGs coupled with multiclass SVM reached 96.4% accuracy for classifying 5 subgroups of MI and healthy controls.

Functional Principal Component Analysis and Randomized Sparse Clustering Algorithm for Medical Image Analysis

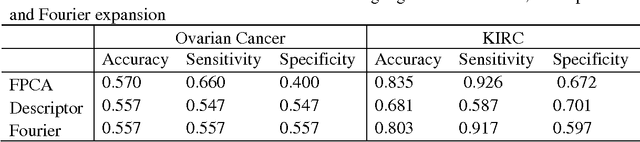
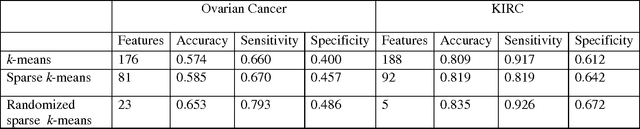
Due to advances in sensors, growing large and complex medical image data have the ability to visualize the pathological change in the cellular or even the molecular level or anatomical changes in tissues and organs. As a consequence, the medical images have the potential to enhance diagnosis of disease, prediction of clinical outcomes, characterization of disease progression, management of health care and development of treatments, but also pose great methodological and computational challenges for representation and selection of features in image cluster analysis. To address these challenges, we first extend one dimensional functional principal component analysis to the two dimensional functional principle component analyses (2DFPCA) to fully capture space variation of image signals. Image signals contain a large number of redundant and irrelevant features which provide no additional or no useful information for cluster analysis. Widely used methods for removing redundant and irrelevant features are sparse clustering algorithms using a lasso-type penalty to select the features. However, the accuracy of clustering using a lasso-type penalty depends on how to select penalty parameters and a threshold for selecting features. In practice, they are difficult to determine. Recently, randomized algorithms have received a great deal of attention in big data analysis. This paper presents a randomized algorithm for accurate feature selection in image cluster analysis. The proposed method is applied to ovarian and kidney cancer histology image data from the TCGA database. The results demonstrate that the randomized feature selection method coupled with functional principal component analysis substantially outperforms the current sparse clustering algorithms in image cluster analysis.

An Efficient Sufficient Dimension Reduction Method for Identifying Genetic Variants of Clinical Significance

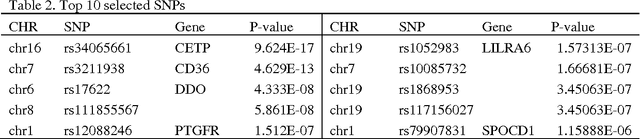
Fast and cheaper next generation sequencing technologies will generate unprecedentedly massive and highly-dimensional genomic and epigenomic variation data. In the near future, a routine part of medical record will include the sequenced genomes. A fundamental question is how to efficiently extract genomic and epigenomic variants of clinical utility which will provide information for optimal wellness and interference strategies. Traditional paradigm for identifying variants of clinical validity is to test association of the variants. However, significantly associated genetic variants may or may not be usefulness for diagnosis and prognosis of diseases. Alternative to association studies for finding genetic variants of predictive utility is to systematically search variants that contain sufficient information for phenotype prediction. To achieve this, we introduce concepts of sufficient dimension reduction and coordinate hypothesis which project the original high dimensional data to very low dimensional space while preserving all information on response phenotypes. We then formulate clinically significant genetic variant discovery problem into sparse SDR problem and develop algorithms that can select significant genetic variants from up to or even ten millions of predictors with the aid of dividing SDR for whole genome into a number of subSDR problems defined for genomic regions. The sparse SDR is in turn formulated as sparse optimal scoring problem, but with penalty which can remove row vectors from the basis matrix. To speed up computation, we develop the modified alternating direction method for multipliers to solve the sparse optimal scoring problem which can easily be implemented in parallel. To illustrate its application, the proposed method is applied to simulation data and the NHLBI's Exome Sequencing Project dataset