Multi-Objective Multi-Fidelity Bayesian Optimization with Causal Priors

Multi-fidelity Bayesian optimization (MFBO) accelerates the search for the global optimum of black-box functions by integrating inexpensive, low-fidelity approximations. The central task of an MFBO policy is to balance the cost-efficiency of low-fidelity proxies against their reduced accuracy to ensure effective progression toward the high-fidelity optimum. Existing MFBO methods primarily capture associational dependencies between inputs, fidelities, and objectives, rather than causal mechanisms, and can perform poorly when lower-fidelity proxies are poorly aligned with the target fidelity. We propose RESCUE (REducing Sampling cost with Causal Understanding and Estimation), a multi-objective MFBO method that incorporates causal calculus to systematically address this challenge. RESCUE learns a structural causal model capturing causal relationships between inputs, fidelities, and objectives, and uses it to construct a probabilistic multi-fidelity (MF) surrogate that encodes intervention effects. Exploiting the causal structure, we introduce a causal hypervolume knowledge-gradient acquisition strategy to select input-fidelity pairs that balance expected multi-objective improvement and cost. We show that RESCUE improves sample efficiency over state-of-the-art MF optimization methods on synthetic and real-world problems in robotics, machine learning (AutoML), and healthcare.

Causally-Aware Information Bottleneck for Domain Adaptation

We tackle a common domain adaptation setting in causal systems. In this setting, the target variable is observed in the source domain but is entirely missing in the target domain. We aim to impute the target variable in the target domain from the remaining observed variables under various shifts. We frame this as learning a compact, mechanism-stable representation. This representation preserves information relevant for predicting the target while discarding spurious variation. For linear Gaussian causal models, we derive a closed-form Gaussian Information Bottleneck (GIB) solution. This solution reduces to a canonical correlation analysis (CCA)-style projection and offers Directed Acyclic Graph (DAG)-aware options when desired. For nonlinear or non-Gaussian data, we introduce a Variational Information Bottleneck (VIB) encoder-predictor. This approach scales to high dimensions and can be trained on source data and deployed zero-shot to the target domain. Across synthetic and real datasets, our approach consistently attains accurate imputations, supporting practical use in high-dimensional causal models and furnishing a unified, lightweight toolkit for causal domain adaptation.

Unicorn: Reasoning about Configurable System Performance through the lens of Causality

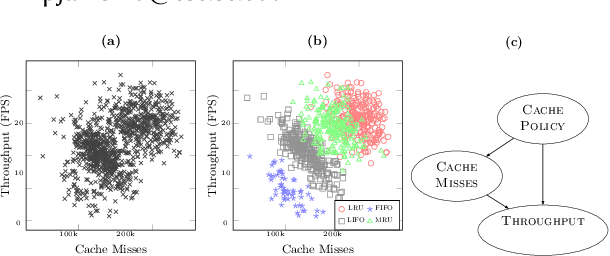
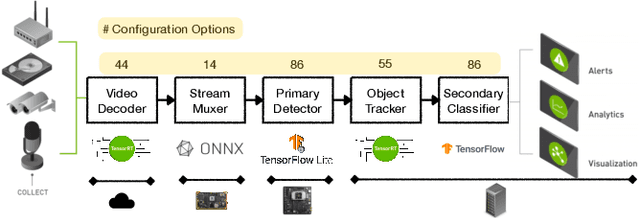
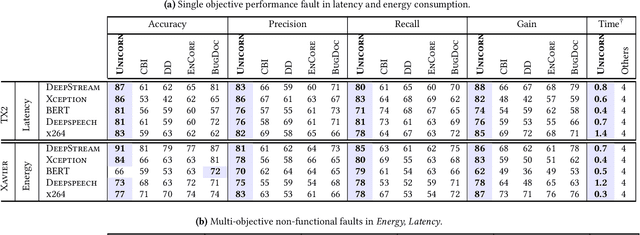
Modern computer systems are highly configurable, with the variability space sometimes larger than the number of atoms in the universe. Understanding and reasoning about the performance behavior of highly configurable systems, due to a vast variability space, is challenging. State-of-the-art methods for performance modeling and analyses rely on predictive machine learning models, therefore, they become (i) unreliable in unseen environments (e.g., different hardware, workloads), and (ii) produce incorrect explanations. To this end, we propose a new method, called Unicorn, which (a) captures intricate interactions between configuration options across the software-hardware stack and (b) describes how such interactions impact performance variations via causal inference. We evaluated Unicorn on six highly configurable systems, including three on-device machine learning systems, a video encoder, a database management system, and a data analytics pipeline. The experimental results indicate that Unicorn outperforms state-of-the-art performance optimization and debugging methods. Furthermore, unlike the existing methods, the learned causal performance models reliably predict performance for new environments.

Learning Circular Hidden Quantum Markov Models: A Tensor Network Approach

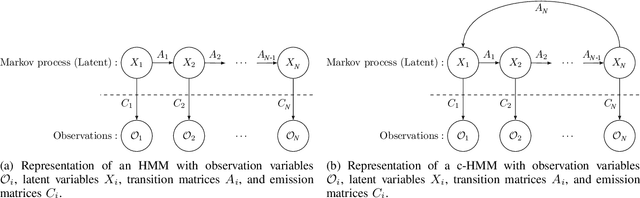
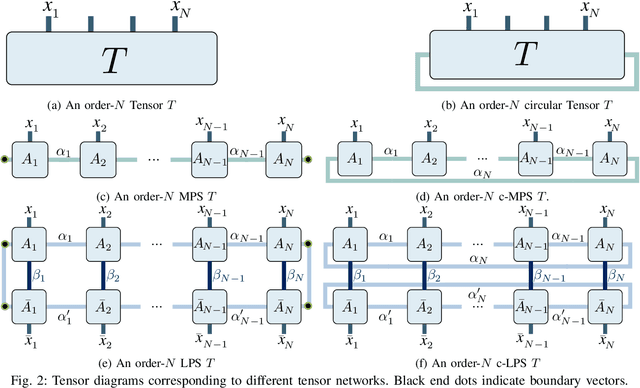
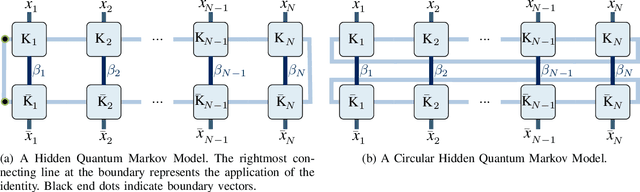
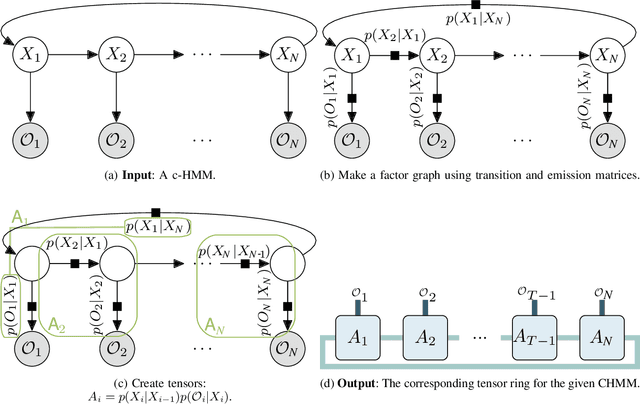
In this paper, we propose circular Hidden Quantum Markov Models (c-HQMMs), which can be applied for modeling temporal data in quantum datasets (with classical datasets as a special case). We show that c-HQMMs are equivalent to a constrained tensor network (more precisely, circular Local Purified State with positive-semidefinite decomposition) model. This equivalence enables us to provide an efficient learning model for c-HQMMs. The proposed learning approach is evaluated on six real datasets and demonstrates the advantage of c-HQMMs on multiple datasets as compared to HQMMs, circular HMMs, and HMMs.

Quantum Causal Inference in the Presence of Hidden Common Causes: an Entropic Approach

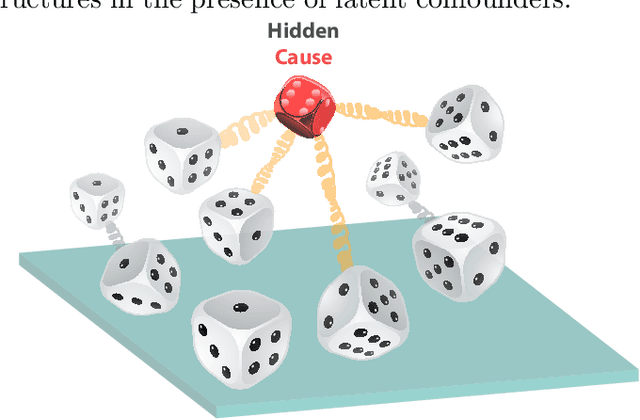
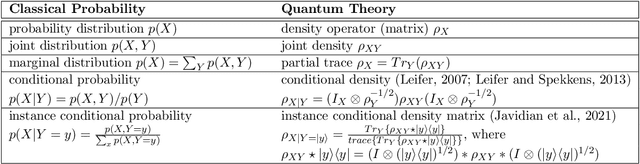
Quantum causality is an emerging field of study which has the potential to greatly advance our understanding of quantum systems. One of the most important problems in quantum causality is linked to this prominent aphorism that states correlation does not mean causation. A direct generalization of the existing causal inference techniques to the quantum domain is not possible due to superposition and entanglement. We put forth a new theoretical framework for merging quantum information science and causal inference by exploiting entropic principles. For this purpose, we leverage the concept of conditional density matrices to develop a scalable algorithmic approach for inferring causality in the presence of latent confounders (common causes) in quantum systems. We apply our proposed framework to an experimentally relevant scenario of identifying message senders on quantum noisy links, where it is validated that the input before noise as a latent confounder is the cause of the noisy outputs. We also demonstrate that the proposed approach outperforms the results of classical causal inference even when the variables are classical by exploiting quantum dependence between variables through density matrices rather than joint probability distributions. Thus, the proposed approach unifies classical and quantum causal inference in a principled way. This successful inference on a synthetic quantum dataset can lay the foundations of identifying originators of malicious activity on future multi-node quantum networks.

Scalable Causal Transfer Learning

One of the most important problems in transfer learning is the task of domain adaptation, where the goal is to apply an algorithm trained in one or more source domains to a different (but related) target domain. This paper deals with domain adaptation in the presence of covariate shift while there exist invariances across domains. A main limitation of existing causal inference methods for solving this problem is scalability. To overcome this difficulty, we propose SCTL, an algorithm that avoids an exhaustive search and identifies invariant causal features across the source and target domains based on Markov blanket discovery. SCTL does not require to have prior knowledge of the causal structure, the type of interventions, or the intervention targets. There is an intrinsic locality associated with SCTL that makes SCTL practically scalable and robust because local causal discovery increases the power of computational independence tests and makes the task of domain adaptation computationally tractable. We show the scalability and robustness of SCTL for domain adaptation using synthetic and real data sets in low-dimensional and high-dimensional settings.

Quantum Entropic Causal Inference

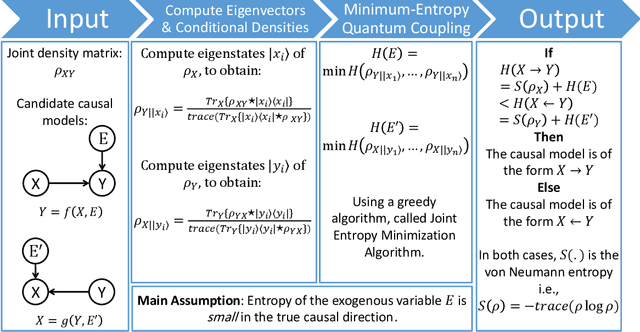
As quantum computing and networking nodes scale-up, important open questions arise on the causal influence of various sub-systems on the total system performance. These questions are related to the tomographic reconstruction of the macroscopic wavefunction and optimizing connectivity of large engineered qubit systems, the reliable broadcasting of information across quantum networks as well as speed-up of classical causal inference algorithms on quantum computers. A direct generalization of the existing causal inference techniques to the quantum domain is not possible due to superposition and entanglement. We put forth a new theoretical framework for merging quantum information science and causal inference by exploiting entropic principles. First, we build the fundamental connection between the celebrated quantum marginal problem and entropic causal inference. Second, inspired by the definition of geometric quantum discord, we fill the gap between classical conditional probabilities and quantum conditional density matrices. These fundamental theoretical advances are exploited to develop a scalable algorithmic approach for quantum entropic causal inference. We apply our proposed framework to an experimentally relevant scenario of identifying message senders on quantum noisy links. This successful inference on a synthetic quantum dataset can lay the foundations of identifying originators of malicious activity on future multi-node quantum networks. We unify classical and quantum causal inference in a principled way paving the way for future applications in quantum computing and networking.

Accelerating Recursive Partition-Based Causal Structure Learning

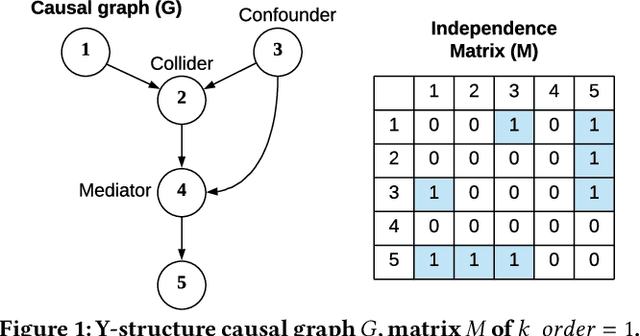
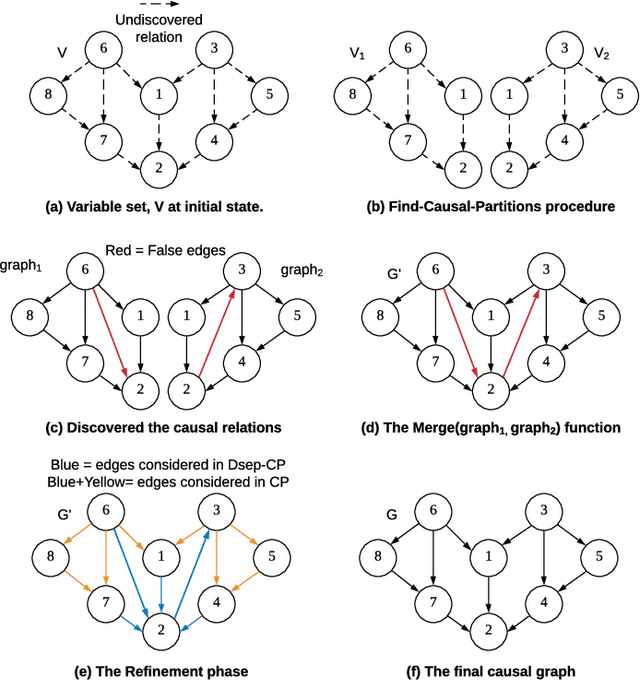
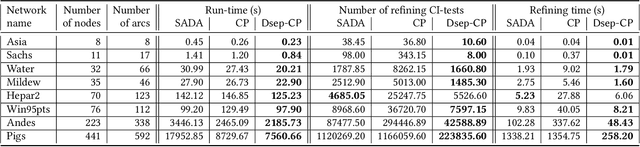
Causal structure discovery from observational data is fundamental to the causal understanding of autonomous systems such as medical decision support systems, advertising campaigns and self-driving cars. This is essential to solve well-known causal decision making and prediction problems associated with those real-world applications. Recently, recursive causal discovery algorithms have gained particular attention among the research community due to their ability to provide good results by using Conditional Independent (CI) tests in smaller sub-problems. However, each of such algorithms needs a refinement function to remove undesired causal relations of the discovered graphs. Notably, with the increase of the problem size, the computation cost (i.e., the number of CI-tests) of the refinement function makes an algorithm expensive to deploy in practice. This paper proposes a generic causal structure refinement strategy that can locate the undesired relations with a small number of CI-tests, thus speeding up the algorithm for large and complex problems. We theoretically prove the correctness of our algorithm. We then empirically evaluate its performance against the state-of-the-art algorithms in terms of solution quality and completion time in synthetic and real datasets.

Learning LWF Chain Graphs: A Markov Blanket Discovery Approach

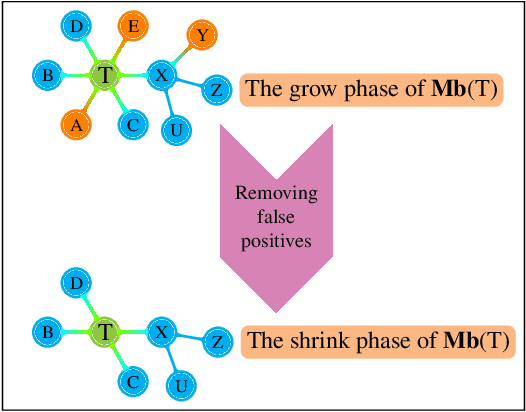
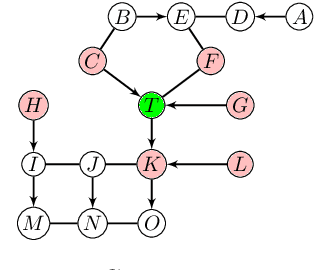
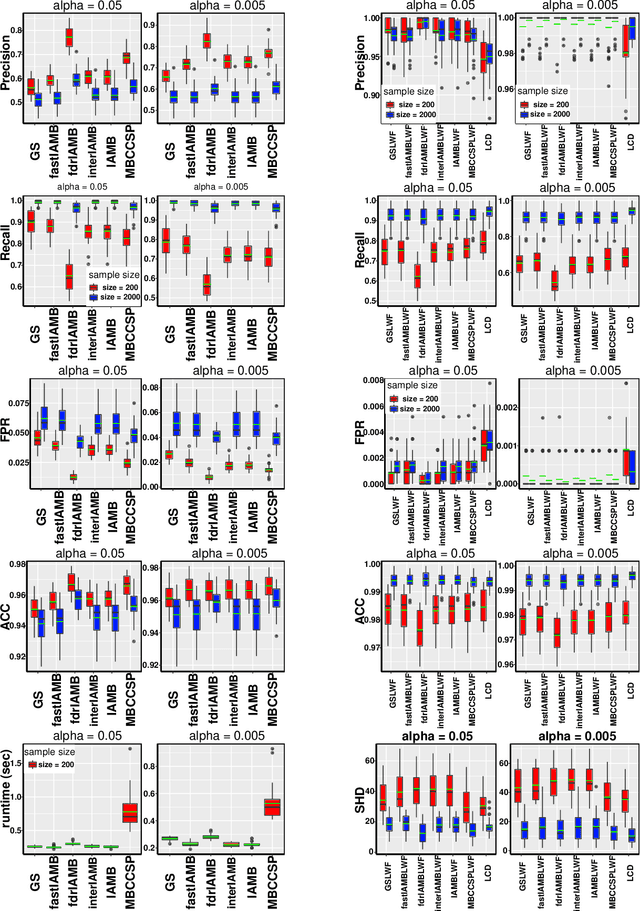
This paper provides a graphical characterization of Markov blankets in chain graphs (CGs) under the Lauritzen-Wermuth-Frydenberg (LWF) interpretation. The characterization is different from the well-known one for Bayesian networks and generalizes it. We provide a novel scalable and sound algorithm for Markov blanket discovery in LWF CGs and prove that the Grow-Shrink algorithm, the IAMB algorithm, and its variants are still correct for Markov blanket discovery in LWF CGs under the same assumptions as for Bayesian networks. We provide a sound and scalable constraint-based framework for learning the structure of LWF CGs from faithful causally sufficient data and prove its correctness when the Markov blanket discovery algorithms in this paper are used. Our proposed algorithms compare positively/competitively against the state-of-the-art LCD (Learn Chain graphs via Decomposition) algorithm, depending on the algorithm that is used for Markov blanket discovery. Our proposed algorithms make a broad range of inference/learning problems computationally tractable and more reliable because they exploit locality.

Learning LWF Chain Graphs: an Order Independent Algorithm

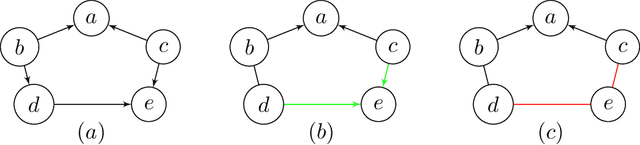
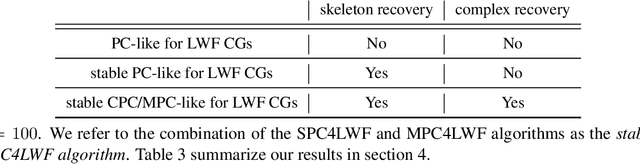
LWF chain graphs combine directed acyclic graphs and undirected graphs. We present a PC-like algorithm that finds the structure of chain graphs under the faithfulness assumption to resolve the problem of scalability of the proposed algorithm by Studeny (1997). We prove that our PC-like algorithm is order dependent, in the sense that the output can depend on the order in which the variables are given. This order dependence can be very pronounced in high-dimensional settings. We propose two modifications of the PC-like algorithm that remove part or all of this order dependence. Simulation results under a variety of settings demonstrate the competitive performance of the PC-like algorithms in comparison with the decomposition-based method, called LCD algorithm, proposed by Ma et al. (2008) in low-dimensional settings and improved performance in high-dimensional settings.