Order-Independent Structure Learning of Multivariate Regression Chain Graphs
Paper and Code
Oct 01, 2019

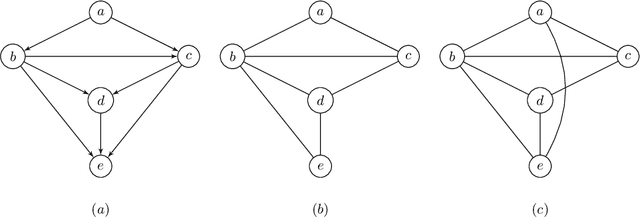
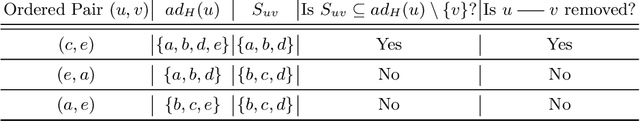
This paper deals with multivariate regression chain graphs (MVR CGs), which were introduced by Cox and Wermuth [3,4] to represent linear causal models with correlated errors. We consider the PC-like algorithm for structure learning of MVR CGs, which is a constraint-based method proposed by Sonntag and Pe\~{n}a in [18]. We show that the PC-like algorithm is order-dependent, in the sense that the output can depend on the order in which the variables are given. This order-dependence is a minor issue in low-dimensional settings. However, it can be very pronounced in high-dimensional settings, where it can lead to highly variable results. We propose two modifications of the PC-like algorithm that remove part or all of this order-dependence. Simulations under a variety of settings demonstrate the competitive performance of our algorithms in comparison with the original PC-like algorithm in low-dimensional settings and improved performance in high-dimensional settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge