Decentralized Cooperation in Heterogeneous Multi-Agent Reinforcement Learning via Graph Neural Network-Based Intrinsic Motivation

Multi-agent Reinforcement Learning (MARL) is emerging as a key framework for various sequential decision-making and control tasks. Unlike their single-agent counterparts, multi-agent systems necessitate successful cooperation among the agents. The deployment of these systems in real-world scenarios often requires decentralized training, a diverse set of agents, and learning from infrequent environmental reward signals. These challenges become more pronounced under partial observability and the lack of prior knowledge about agent heterogeneity. While notable studies use intrinsic motivation (IM) to address reward sparsity or cooperation in decentralized settings, those dealing with heterogeneity typically assume centralized training, parameter sharing, and agent indexing. To overcome these limitations, we propose the CoHet algorithm, which utilizes a novel Graph Neural Network (GNN) based intrinsic motivation to facilitate the learning of heterogeneous agent policies in decentralized settings, under the challenges of partial observability and reward sparsity. Evaluation of CoHet in the Multi-agent Particle Environment (MPE) and Vectorized Multi-Agent Simulator (VMAS) benchmarks demonstrates superior performance compared to the state-of-the-art in a range of cooperative multi-agent scenarios. Our research is supplemented by an analysis of the impact of the agent dynamics model on the intrinsic motivation module, insights into the performance of different CoHet variants, and its robustness to an increasing number of heterogeneous agents.

Blind Image Deblurring using FFT-ReLU with Deep Learning Pipeline Integration

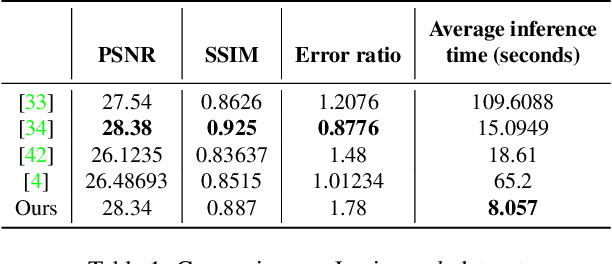
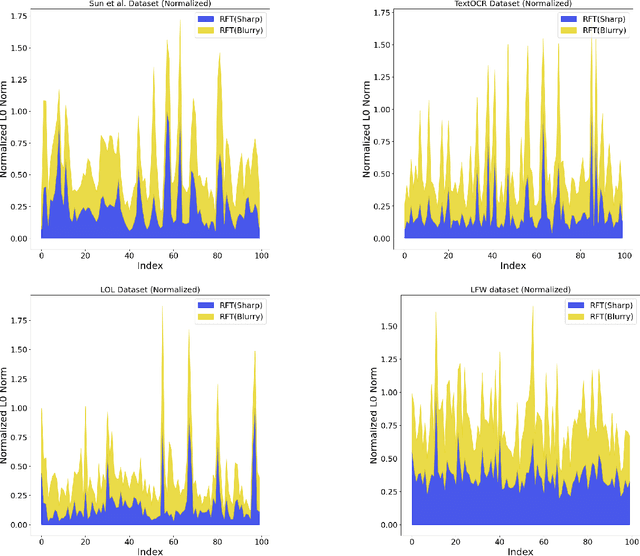
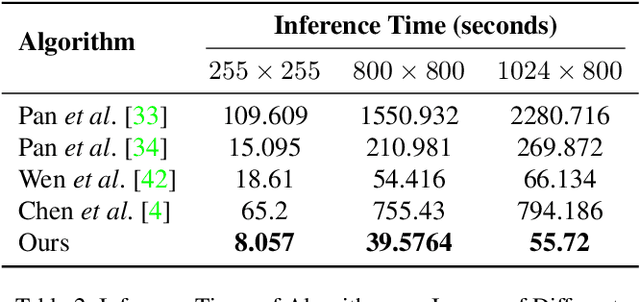
Blind image deblurring is the process of deriving a sharp image and a blur kernel from a blurred image. Blurry images are typically modeled as the convolution of a sharp image with a blur kernel, necessitating the estimation of the unknown blur kernel to perform blind image deblurring effectively. Existing approaches primarily focus on domain-specific features of images, such as salient edges, dark channels, and light streaks. These features serve as probabilistic priors to enhance the estimation of the blur kernel. For improved generality, we propose a novel prior (ReLU sparsity prior) that estimates blur kernel effectively across all distributions of images (natural, facial, text, low-light, saturated etc). Our approach demonstrates superior efficiency, with inference times up to three times faster, while maintaining high accuracy in PSNR, SSIM, and error ratio metrics. We also observe noticeable improvement in the performance of the state-of-the-art architectures (in terms of aforementioned metrics) in deep learning based approaches when our method is used as a post-processing unit.

A Graph Neural Network-Based QUBO-Formulated Hamiltonian-Inspired Loss Function for Combinatorial Optimization using Reinforcement Learning

Quadratic Unconstrained Binary Optimization (QUBO) is a generic technique to model various NP-hard Combinatorial Optimization problems (CO) in the form of binary variables. Ising Hamiltonian is used to model the energy function of a system. QUBO to Ising Hamiltonian is regarded as a technique to solve various canonical optimization problems through quantum optimization algorithms. Recently, PI-GNN, a generic framework, has been proposed to address CO problems over graphs based on Graph Neural Network (GNN) architecture. They introduced a generic QUBO-formulated Hamiltonian-inspired loss function that was directly optimized using GNN. PI-GNN is highly scalable but there lies a noticeable decrease in the number of satisfied constraints when compared to problem-specific algorithms and becomes more pronounced with increased graph densities. Here, We identify a behavioral pattern related to it and devise strategies to improve its performance. Another group of literature uses Reinforcement learning (RL) to solve the aforementioned NP-hard problems using problem-specific reward functions. In this work, we also focus on creating a bridge between the RL-based solutions and the QUBO-formulated Hamiltonian. We formulate and empirically evaluate the compatibility of the QUBO-formulated Hamiltonian as the generic reward function in the RL-based paradigm in the form of rewards. Furthermore, we also introduce a novel Monty Carlo Tree Search-based strategy with GNN where we apply a guided search through manual perturbation of node labels during training. We empirically evaluated our methods and observed up to 44% improvement in the number of constraint violations compared to the PI-GNN.

DePAint: A Decentralized Safe Multi-Agent Reinforcement Learning Algorithm considering Peak and Average Constraints

The field of safe multi-agent reinforcement learning, despite its potential applications in various domains such as drone delivery and vehicle automation, remains relatively unexplored. Training agents to learn optimal policies that maximize rewards while considering specific constraints can be challenging, particularly in scenarios where having a central controller to coordinate the agents during the training process is not feasible. In this paper, we address the problem of multi-agent policy optimization in a decentralized setting, where agents communicate with their neighbors to maximize the sum of their cumulative rewards while also satisfying each agent's safety constraints. We consider both peak and average constraints. In this scenario, there is no central controller coordinating the agents and both the rewards and constraints are only known to each agent locally/privately. We formulate the problem as a decentralized constrained multi-agent Markov Decision Problem and propose a momentum-based decentralized policy gradient method, DePAint, to solve it. To the best of our knowledge, this is the first privacy-preserving fully decentralized multi-agent reinforcement learning algorithm that considers both peak and average constraints. We also provide theoretical analysis and empirical evaluation of our algorithm in various scenarios and compare its performance to centralized algorithms that consider similar constraints.

Understanding the Usage of QUBO-based Hamiltonian Function in Combinatorial Optimization over Graphs: A Discussion Using Max Cut (MC) Problem

Quadratic Unconstrained Binary Optimization (QUBO) is a generic technique to model various NP-hard combinatorial optimization problems in the form of binary variables. The Hamiltonian function is often used to formulate QUBO problems where it is used as the objective function in the context of optimization. In this study, we investigate how reinforcement learning-based (RL) paradigms with the presence of the Hamiltonian function can address combinatorial optimization problems over graphs in QUBO formulations. We use Graph Neural Network (GNN) as the message-passing architecture to convey the information among the nodes. We have centered our discussion on QUBO formulated Max-Cut problem but the intuitions can be extended to any QUBO supported canonical NP-Hard combinatorial optimization problems. We mainly investigate three formulations, Monty-Carlo Tree Search with GNN-based RL (MCTS-GNN), DQN with GNN-based RL, and a generic GNN with attention-based RL (GRL). Our findings state that in the RL-based paradigm, the Hamiltonian function-based optimization in QUBO formulation brings model convergence and can be used as a generic reward function. We also analyze and present the performance of our RL-based setups through experimenting over graphs of different densities and compare them with a simple GNN-based setup in the light of constraint violation, learning stability and computation cost. As per one of our findings, all the architectures provide a very comparable performance in sparse graphs as per the number of constraint violation whreas MCTS-GNN gives the best performance. In the similar criteria, the performance significantly starts to drop both for GRL and simple GNN-based setups whereas MCTS-GNN and DQN shines. We also present the corresponding mathematical formulations and in-depth discussion of the observed characteristics during experimentations.

Improving Causal Effect Estimation of Weighted RegressionBased Estimator using Neural Networks

Estimating causal effects from observational data informs us about which factors are important in an autonomous system, and enables us to take better decisions. This is important because it has applications in selecting a treatment in medical systems or making better strategies in industries or making better policies for our government or even the society. Unavailability of complete data, coupled with high cardinality of data, makes this estimation task computationally intractable. Recently, a regression-based weighted estimator has been introduced that is capable of producing solution using bounded samples of a given problem. However, as the data dimension increases, the solution produced by the regression-based method degrades. Against this background, we introduce a neural network based estimator that improves the solution quality in case of non-linear and finitude of samples. Finally, our empirical evaluation illustrates a significant improvement of solution quality, up to around $55\%$, compared to the state-of-the-art estimators.

Learning Cooperation and Online Planning Through Simulation and Graph Convolutional Network

Multi-agent Markov Decision Process (MMDP) has been an effective way of modelling sequential decision making algorithms for multi-agent cooperative environments. A number of algorithms based on centralized and decentralized planning have been developed in this domain. However, dynamically changing environment, coupled with exponential size of the state and joint action space, make it difficult for these algorithms to provide both efficiency and scalability. Recently, Centralized planning algorithm FV-MCTS-MP and decentralized planning algorithm \textit{Alternate maximization with Behavioural Cloning} (ABC) have achieved notable performance in solving MMDPs. However, they are not capable of adapting to dynamically changing environments and accounting for the lack of communication among agents, respectively. Against this background, we introduce a simulation based online planning algorithm, that we call SiCLOP, for multi-agent cooperative environments. Specifically, SiCLOP tailors Monte Carlo Tree Search (MCTS) and uses Coordination Graph (CG) and Graph Neural Network (GCN) to learn cooperation and provides real time solution of a MMDP problem. It also improves scalability through an effective pruning of action space. Additionally, unlike FV-MCTS-MP and ABC, SiCLOP supports transfer learning, which enables learned agents to operate in different environments. We also provide theoretical discussion about the convergence property of our algorithm within the context of multi-agent settings. Finally, our extensive empirical results show that SiCLOP significantly outperforms the state-of-the-art online planning algorithms.

Accelerating Recursive Partition-Based Causal Structure Learning

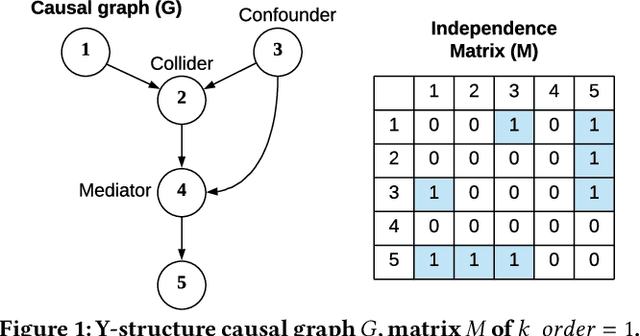
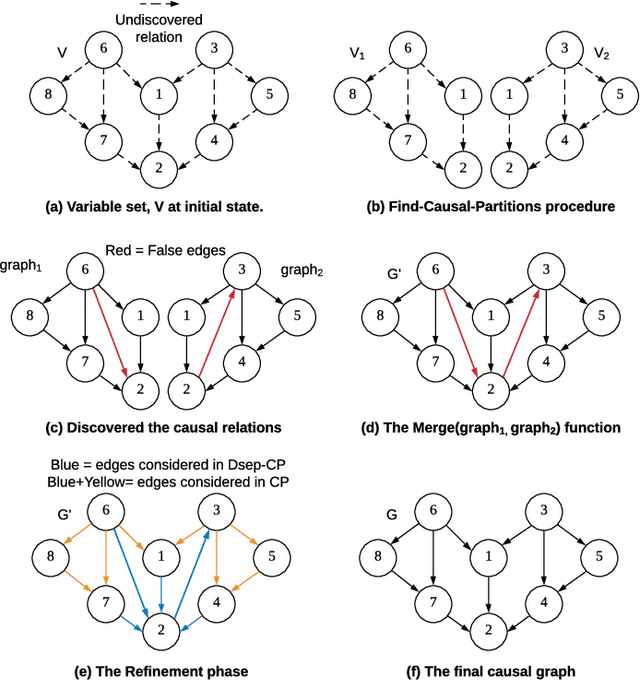
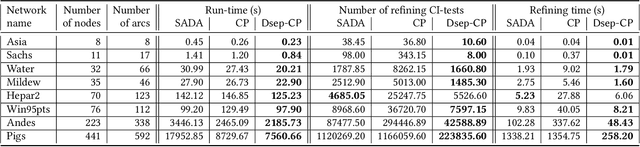
Causal structure discovery from observational data is fundamental to the causal understanding of autonomous systems such as medical decision support systems, advertising campaigns and self-driving cars. This is essential to solve well-known causal decision making and prediction problems associated with those real-world applications. Recently, recursive causal discovery algorithms have gained particular attention among the research community due to their ability to provide good results by using Conditional Independent (CI) tests in smaller sub-problems. However, each of such algorithms needs a refinement function to remove undesired causal relations of the discovered graphs. Notably, with the increase of the problem size, the computation cost (i.e., the number of CI-tests) of the refinement function makes an algorithm expensive to deploy in practice. This paper proposes a generic causal structure refinement strategy that can locate the undesired relations with a small number of CI-tests, thus speeding up the algorithm for large and complex problems. We theoretically prove the correctness of our algorithm. We then empirically evaluate its performance against the state-of-the-art algorithms in terms of solution quality and completion time in synthetic and real datasets.

Improving Solution Quality of Bounded Max-Sum Algorithm to Solve DCOPs involving Hard and Soft Constraints

Bounded Max-Sum (BMS) is a message-passing algorithm that provides approximation solution to a specific form of de-centralized coordination problems, namely Distributed Constrained Optimization Problems (DCOPs). In particular, BMS algorithm is able to solve problems of this type having large search space at the expense of low computational cost. Notably, the traditional DCOP formulation does not consider those constraints that must be satisfied(also known as hard constraints), rather it concentrates only on soft constraints. Hence, although the presence of both types of constraints are observed in a number of real-world applications, the BMS algorithm does not actively capitalize on the hard constraints. To address this issue, we tailor BMS in such a way that can deal with DCOPs having both type constraints. In so doing, our approach improves the solution quality of the algorithm. The empirical results exhibit a marked improvement in the quality of the solutions of large DCOPs.

A Particle Swarm Inspired Approach for Continuous Distributed Constraint Optimization Problems

Distributed Constraint Optimization Problems (DCOPs) are a widely studied framework for coordinating interactions in cooperative multi-agent systems. In classical DCOPs, variables owned by agents are assumed to be discrete. However, in many applications, such as target tracking or sleep scheduling in sensor networks, continuous-valued variables are more suitable than discrete ones. To better model such applications, researchers have proposed Continuous DCOPs (C-DCOPs), an extension of DCOPs, that can explicitly model problems with continuous variables. The state-of-the-art approaches for solving C-DCOPs experience either onerous memory or computation overhead and unsuitable for non-differentiable optimization problems. To address this issue, we propose a new C-DCOP algorithm, namely Particle Swarm Optimization Based C-DCOP (PCD), which is inspired by Particle Swarm Optimization (PSO), a well-known centralized population-based approach for solving continuous optimization problems. In recent years, population-based algorithms have gained significant attention in classical DCOPs due to their ability in producing high-quality solutions. Nonetheless, to the best of our knowledge, this class of algorithms has not been utilized to solve C-DCOPs and there has been no work evaluating the potential of PSO in solving classical DCOPs or C-DCOPs. In light of this observation, we adapted PSO, a centralized algorithm, to solve C-DCOPs in a decentralized manner. The resulting PCD algorithm not only produces good-quality solutions but also finds solutions without any requirement for derivative calculations. Moreover, we design a crossover operator that can be used by PCD to further improve the quality of solutions found. Finally, we theoretically prove that PCD is an anytime algorithm and empirically evaluate PCD against the state-of-the-art C-DCOP algorithms in a wide variety of benchmarks.