Learning LWF Chain Graphs: A Markov Blanket Discovery Approach
Paper and Code
May 29, 2020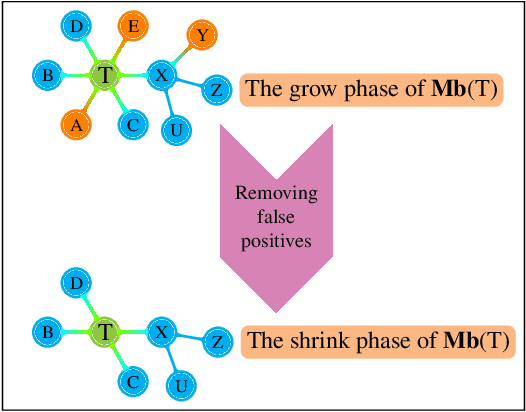
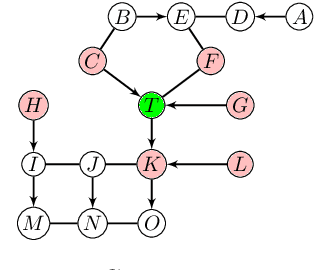
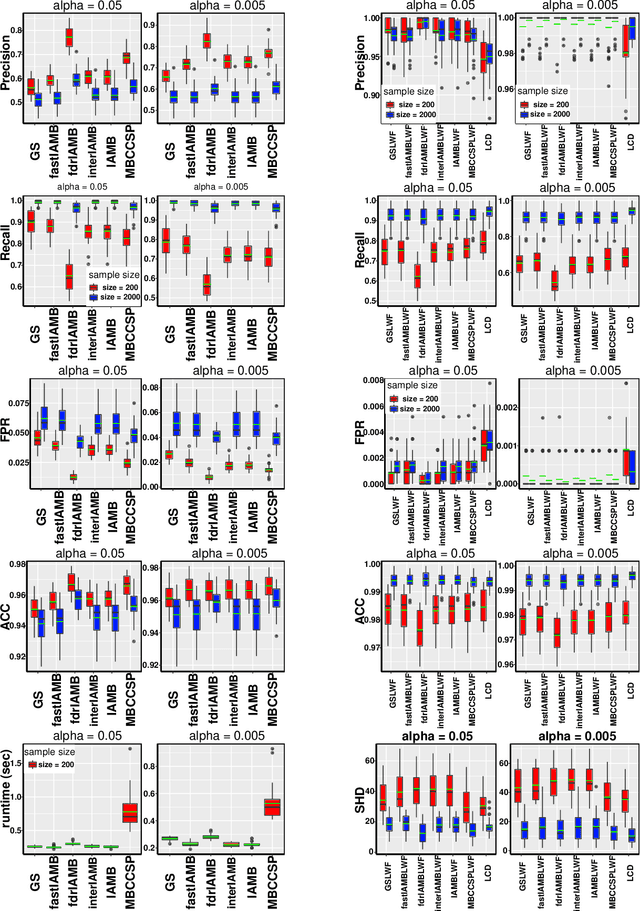
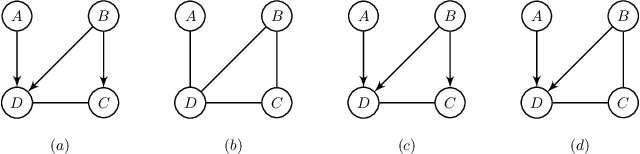
This paper provides a graphical characterization of Markov blankets in chain graphs (CGs) under the Lauritzen-Wermuth-Frydenberg (LWF) interpretation. The characterization is different from the well-known one for Bayesian networks and generalizes it. We provide a novel scalable and sound algorithm for Markov blanket discovery in LWF CGs and prove that the Grow-Shrink algorithm, the IAMB algorithm, and its variants are still correct for Markov blanket discovery in LWF CGs under the same assumptions as for Bayesian networks. We provide a sound and scalable constraint-based framework for learning the structure of LWF CGs from faithful causally sufficient data and prove its correctness when the Markov blanket discovery algorithms in this paper are used. Our proposed algorithms compare positively/competitively against the state-of-the-art LCD (Learn Chain graphs via Decomposition) algorithm, depending on the algorithm that is used for Markov blanket discovery. Our proposed algorithms make a broad range of inference/learning problems computationally tractable and more reliable because they exploit locality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge