Lossy compression of matrices by black-box optimisation of mixed-integer non-linear programming

In edge computing, suppressing data size is a challenge for machine learning models that perform complex tasks such as autonomous driving, in which computational resources (speed, memory size and power) are limited. Efficient lossy compression of matrix data has been introduced by decomposing it into the product of an integer and real matrices. However, its optimisation is difficult as it requires simultaneous optimisation of an integer and real variables. In this paper, we improve this optimisation by utilising recently developed black-box optimisation (BBO) algorithms with an Ising solver for integer variables. In addition, the algorithm can be used to solve mixed-integer programming problems that are linear and non-linear in terms of real and integer variables, respectively. The differences between the choice of Ising solvers (simulated annealing (SA), quantum annealing (QA) and simulated quenching (SQ)) and the strategies of the BBO algorithms (BOCS, FMQA and their variations) are discussed for further development of the BBO techniques.

Canonical and Compact Point Cloud Representation for Shape Classification

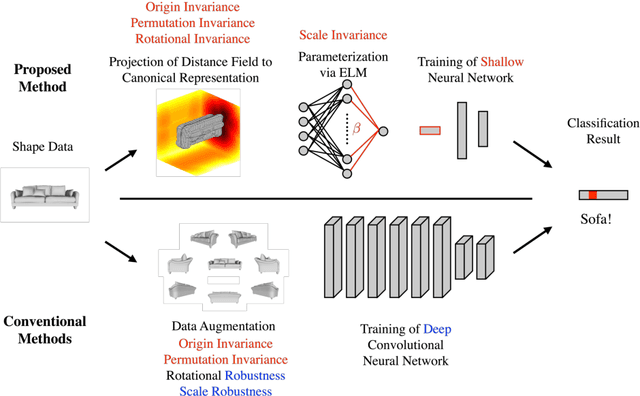
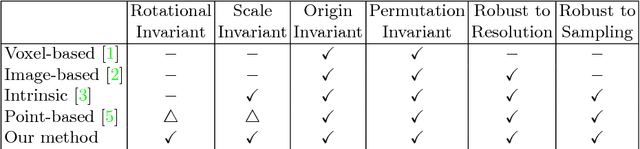
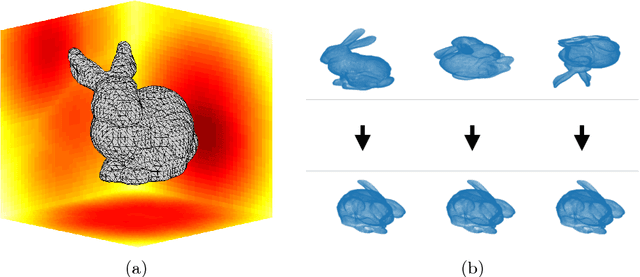
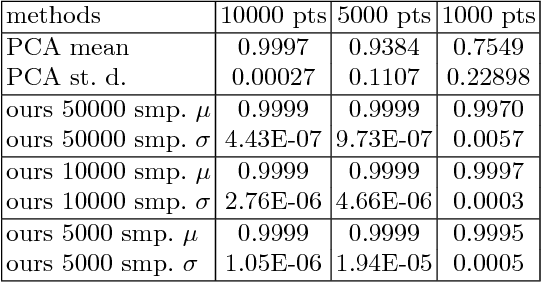
We present a novel compact point cloud representation that is inherently invariant to scale, coordinate change and point permutation. The key idea is to parametrize a distance field around an individual shape into a unique, canonical, and compact vector in an unsupervised manner. We firstly project a distance field to a $4$D canonical space using singular value decomposition. We then train a neural network for each instance to non-linearly embed its distance field into network parameters. We employ a bias-free Extreme Learning Machine (ELM) with ReLU activation units, which has scale-factor commutative property between layers. We demonstrate the descriptiveness of the instance-wise, shape-embedded network parameters by using them to classify shapes in $3$D datasets. Our learning-based representation requires minimal augmentation and simple neural networks, where previous approaches demand numerous representations to handle coordinate change and point permutation.

Binary-decomposed DCNN for accelerating computation and compressing model without retraining

Recent trends show recognition accuracy increasing even more profoundly. Inference process of Deep Convolutional Neural Networks (DCNN) has a large number of parameters, requires a large amount of computation, and can be very slow. The large number of parameters also require large amounts of memory. This is resulting in increasingly long computation times and large model sizes. To implement mobile and other low performance devices incorporating DCNN, model sizes must be compressed and computation must be accelerated. To that end, this paper proposes Binary-decomposed DCNN, which resolves these issues without the need for retraining. Our method replaces real-valued inner-product computations with binary inner-product computations in existing network models to accelerate computation of inference and decrease model size without the need for retraining. Binary computations can be done at high speed using logical operators such as XOR and AND, together with bit counting. In tests using AlexNet with the ImageNet classification task, speed increased by a factor of 1.79, models were compressed by approximately 80%, and increase in error rate was limited to 1.20%. With VGG-16, speed increased by a factor of 2.07, model sizes decreased by 81%, and error increased by only 2.16%.

Fast Supervised Discrete Hashing and its Analysis

In this paper, we propose a learning-based supervised discrete hashing method. Binary hashing is widely used for large-scale image retrieval as well as video and document searches because the compact representation of binary code is essential for data storage and reasonable for query searches using bit-operations. The recently proposed Supervised Discrete Hashing (SDH) efficiently solves mixed-integer programming problems by alternating optimization and the Discrete Cyclic Coordinate descent (DCC) method. We show that the SDH model can be simplified without performance degradation based on some preliminary experiments; we call the approximate model for this the "Fast SDH" (FSDH) model. We analyze the FSDH model and provide a mathematically exact solution for it. In contrast to SDH, our model does not require an alternating optimization algorithm and does not depend on initial values. FSDH is also easier to implement than Iterative Quantization (ITQ). Experimental results involving a large-scale database showed that FSDH outperforms conventional SDH in terms of precision, recall, and computation time.

Pairwise Rotation Hashing for High-dimensional Features

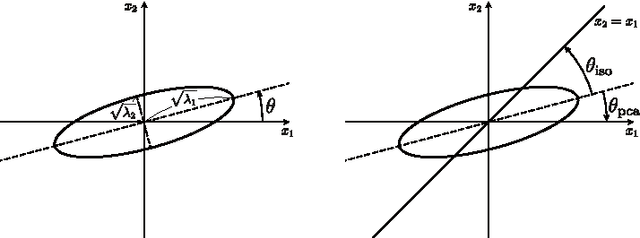
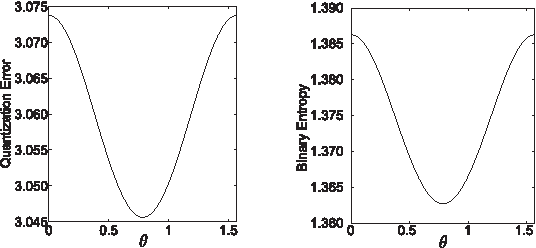
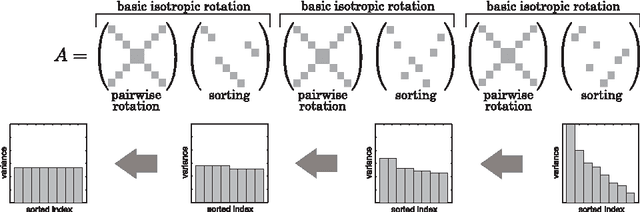
Binary Hashing is widely used for effective approximate nearest neighbors search. Even though various binary hashing methods have been proposed, very few methods are feasible for extremely high-dimensional features often used in visual tasks today. We propose a novel highly sparse linear hashing method based on pairwise rotations. The encoding cost of the proposed algorithm is $\mathrm{O}(n \log n)$ for n-dimensional features, whereas that of the existing state-of-the-art method is typically $\mathrm{O}(n^2)$. The proposed method is also remarkably faster in the learning phase. Along with the efficiency, the retrieval accuracy is comparable to or slightly outperforming the state-of-the-art. Pairwise rotations used in our method are formulated from an analytical study of the trade-off relationship between quantization error and entropy of binary codes. Although these hashing criteria are widely used in previous researches, its analytical behavior is rarely studied. All building blocks of our algorithm are based on the analytical solution, and it thus provides a fairly simple and efficient procedure.