Pairwise Rotation Hashing for High-dimensional Features
Paper and Code
Jan 29, 2015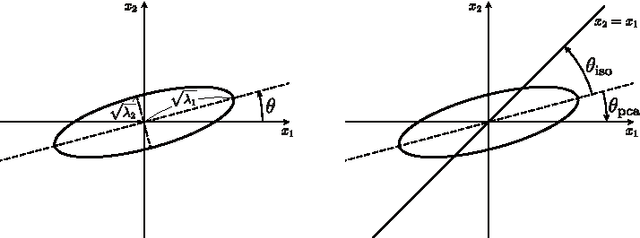

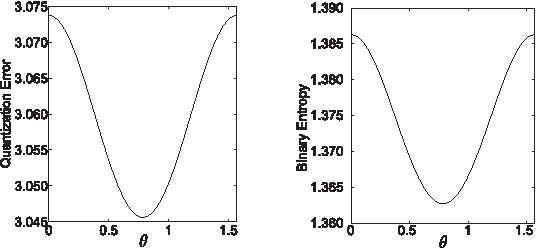
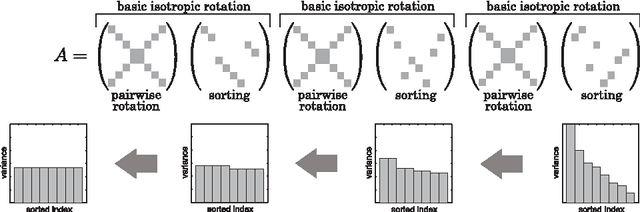
Binary Hashing is widely used for effective approximate nearest neighbors search. Even though various binary hashing methods have been proposed, very few methods are feasible for extremely high-dimensional features often used in visual tasks today. We propose a novel highly sparse linear hashing method based on pairwise rotations. The encoding cost of the proposed algorithm is $\mathrm{O}(n \log n)$ for n-dimensional features, whereas that of the existing state-of-the-art method is typically $\mathrm{O}(n^2)$. The proposed method is also remarkably faster in the learning phase. Along with the efficiency, the retrieval accuracy is comparable to or slightly outperforming the state-of-the-art. Pairwise rotations used in our method are formulated from an analytical study of the trade-off relationship between quantization error and entropy of binary codes. Although these hashing criteria are widely used in previous researches, its analytical behavior is rarely studied. All building blocks of our algorithm are based on the analytical solution, and it thus provides a fairly simple and efficient procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge