On the Rashomon ratio of infinite hypothesis sets

Given a classification problem and a family of classifiers, the Rashomon ratio measures the proportion of classifiers that yield less than a given loss. Previous work has explored the advantage of a large Rashomon ratio in the case of a finite family of classifiers. Here we consider the more general case of an infinite family. We show that a large Rashomon ratio guarantees that choosing the classifier with the best empirical accuracy among a random subset of the family, which is likely to improve generalizability, will not increase the empirical loss too much. We quantify the Rashomon ratio in two examples involving infinite classifier families in order to illustrate situations in which it is large. In the first example, we estimate the Rashomon ratio of the classification of normally distributed classes using an affine classifier. In the second, we obtain a lower bound for the Rashomon ratio of a classification problem with a modified Gram matrix when the classifier family consists of two-layer ReLU neural networks. In general, we show that the Rashomon ratio can be estimated using a training dataset along with random samples from the classifier family and we provide guarantees that such an estimation is close to the true value of the Rashomon ratio.

Path Tracking using Echoes in an Unknown Environment: the Issue of Symmetries and How to Break Them

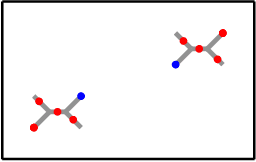
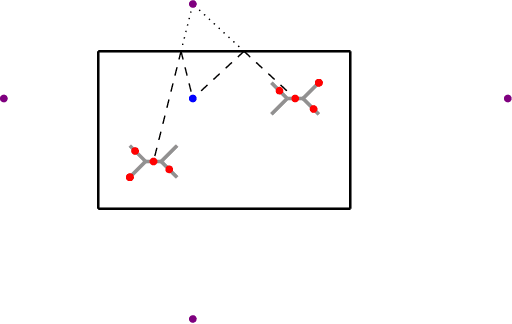
This paper deals with the problem of reconstructing the path of a vehicle in an unknown environment consisting of planar structures using sound. Many systems in the literature do this by using a loudspeaker and microphones mounted on a vehicle. Symmetries in the environment lead to solution ambiguities for such systems. We propose to resolve this issue by placing the loudspeaker at a fixed location in the environment rather than on the vehicle. The question of whether this will remove ambiguities regardless of the environment geometry leads to a question about breaking symmetries that can be phrased in purely mathematical terms. We solve this question in the affirmative if the geometry is in dimension three or bigger, and give counterexamples in dimension two. Excluding the rare situations where the counterexamples arise, we also give an affirmative answer in dimension two. Our results lead to a simple path reconstruction algorithm for a vehicle carrying four microphones navigating within an environment in which a loudspeaker at a fixed position emits short bursts of sounds. This algorithm could be combined with other methods from the literature to construct a path tracking system for vehicles navigating within a potentially symmetric environment.

Global Positioning: the Uniqueness Question and a New Solution Method

We provide a new algebraic solution procedure for the global positioning problem in $n$ dimensions using $m$ satellites. We also give a geometric characterization of the situations in which the problem does not have a unique solution. This characterization shows that such cases can happen in any dimension and with any number of satellites, leading to counterexamples to some open conjectures. We fill a gap in the literature by giving a proof for the long-held belief that when $m \ge n+2$, the solution is unique for almost all user positions. Even better, when $m \ge 2n+2$, almost all satellite configurations will guarantee a unique solution for all user positions. Some of our results are obtained using tools from algebraic geometry.

Multilateration and Signal Matching with Unknown Emission Times

Assume that a source emits a signal in $3$-dimensional space at an unknown time, which is received by at least~$5$ sensors. In almost all cases the emission time and source position can be worked out uniquely from the knowledge of the times when the sensors receive the signal. The task to do so is the multilateration problem. But when there are several emission events originating from several sources, the received signals must first be matched in order to find the emission times and source positions. In this paper, we propose to use algebraic relations between reception times to achieve this matching. A special case occurs when the signals are actually echoes from a single emission event. In this case, solving the signal matching problem allows one to reconstruct the positions of the reflecting walls. We show that, no matter where the walls are situated, our matching algorithm works correctly for almost all positions of the sensors. In the first section of this paper we consider the multilateration problem, which is equivalent to the GPS-problem, and give a simple algebraic solution that applies in all dimensions.

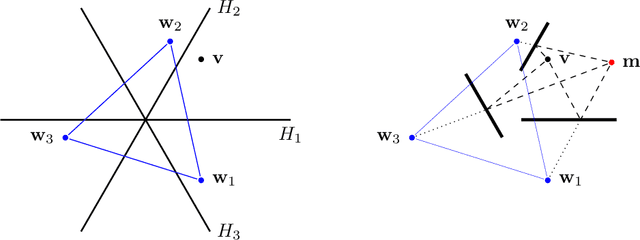
Can a Ground-Based Vehicle Hear the Shape of a Room?

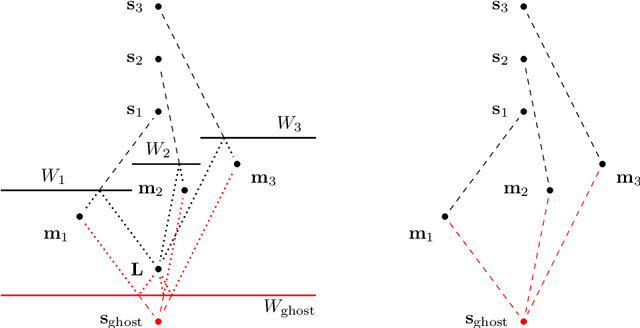
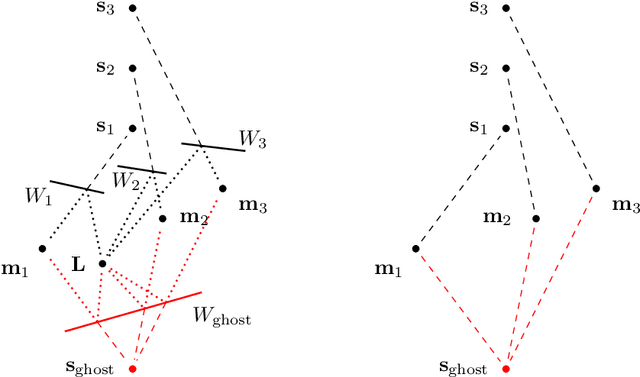
Assume that a ground-based vehicle moves in a room with walls or other planar surfaces. Can the vehicle reconstruct the positions of the walls from the echoes of a single sound event? We assume that the vehicle carries some microphones and that a loudspeaker is either also mounted on the vehicle or placed at a fixed location in the room. We prove that the reconstruction is almost always possible if (1) no echoes are received from floors, ceilings or sloping walls and the vehicle carries at least three non-collinear microphones, or if (2) walls of any inclination may occur, the loudspeaker is fixed in the room and there are four non-coplanar microphones. The difficulty lies in the echo-matching problem: how to determine which echoes come from the same wall. We solve this by using a Cayley-Menger determinant. Our proofs use methods from computational commutative algebra.

Asymptotic optimality and minimal complexity of classification by random projection

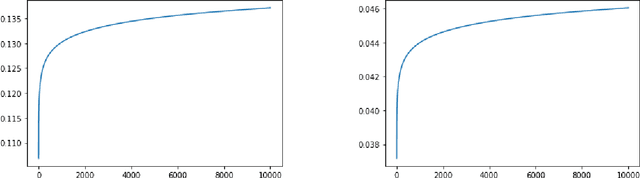
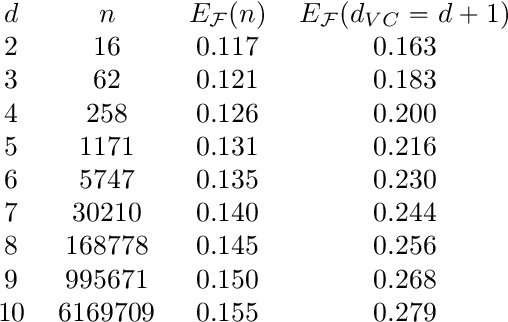
The generalization error of a classifier is related to the complexity of the set of functions among which the classifier is chosen. Roughly speaking, the more complex the family, the greater the potential disparity between the training error and the population error of the classifier. This principle is embodied in layman's terms by Occam's razor principle, which suggests favoring low-complexity hypotheses over complex ones. We study a family of low-complexity classifiers consisting of thresholding the one-dimensional feature obtained by projecting the data on a random line after embedding it into a higher dimensional space parametrized by monomials of order up to k. More specifically, the extended data is projected n-times and the best classifier among those n (based on its performance on training data) is chosen. We obtain a bound on the generalization error of these low-complexity classifiers. The bound is less than that of any classifier with a non-trivial VC dimension, and thus less than that of a linear classifier. We also show that, given full knowledge of the class conditional densities, the error of the classifiers would converge to the optimal (Bayes) error as k and n go to infinity; if only a training dataset is given, we show that the classifiers will perfectly classify all the training points as k and n go to infinity.

Clustering small datasets in high-dimension by random projection

Datasets in high-dimension do not typically form clusters in their original space; the issue is worse when the number of points in the dataset is small. We propose a low-computation method to find statistically significant clustering structures in a small dataset. The method proceeds by projecting the data on a random line and seeking binary clusterings in the resulting one-dimensional data. Non-linear separations are obtained by extending the feature space using monomials of higher degrees in the original features. The statistical validity of the clustering structures obtained is tested in the projected one-dimensional space, thus bypassing the challenge of statistical validation in high-dimension. Projecting on a random line is an extreme dimension reduction technique that has previously been used successfully as part of a hierarchical clustering method for high-dimensional data. Our experiments show that with this simplified framework, statistically significant clustering structures can be found with as few as 100-200 points, depending on the dataset. The different structures uncovered are found to persist as more points are added to the dataset.

A highly likely clusterable data model with no clusters

We propose a model for a dataset in ${\mathbb R}^D$ that does not contain any clusters but yet is such that a projection of the points on a random one-dimensional subspace is likely to yield a clustering of the points. This model is compatible with some recent empirical observations.

Three Efficient, Low-Complexity Algorithms for Automatic Color Trapping

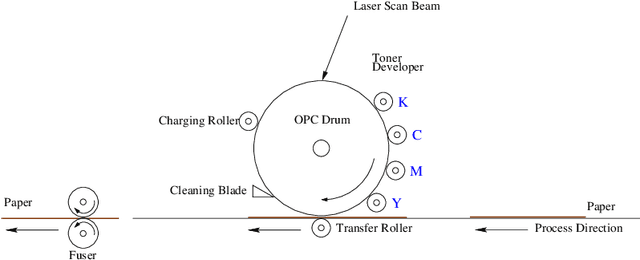
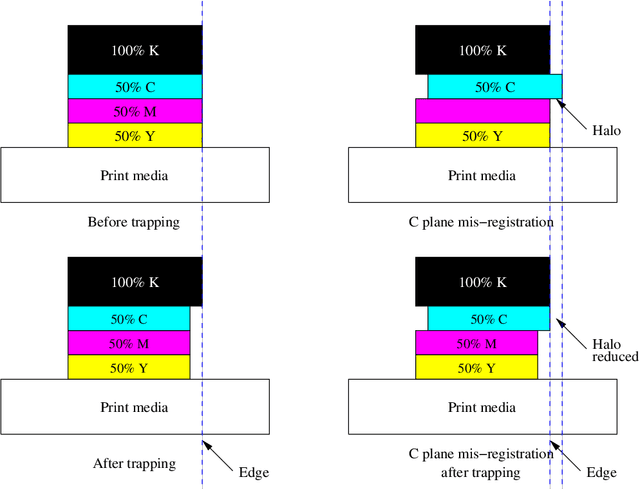
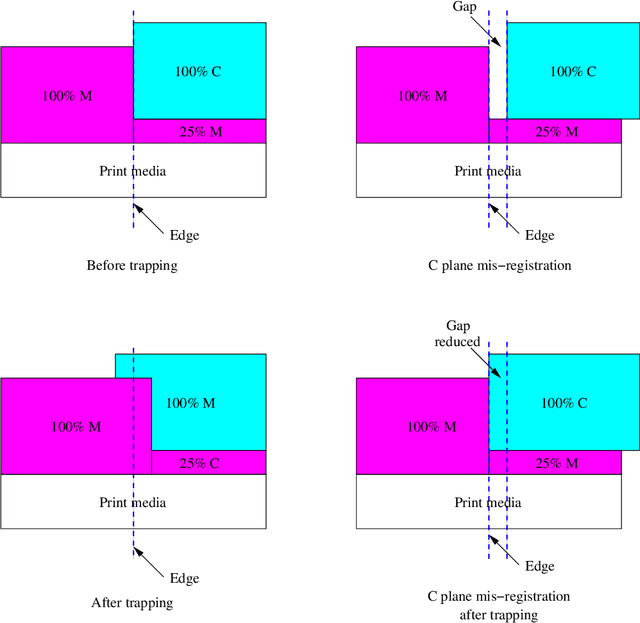
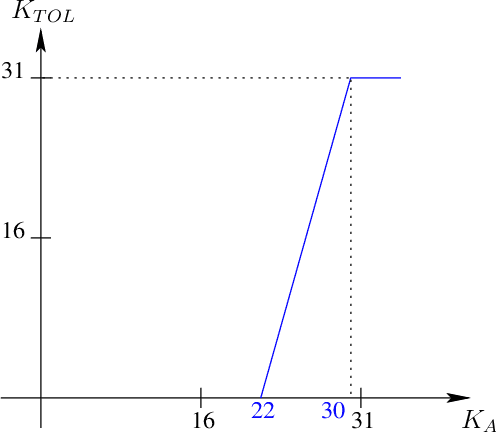
Color separations (most often cyan, magenta, yellow, and black) are commonly used in printing to reproduce multi-color images. For mechanical reasons, these color separations are generally not perfectly aligned with respect to each other when they are rendered by their respective imaging stations. This phenomenon, called color plane misregistration, causes gap and halo artifacts in the printed image. Color trapping is an image processing technique that aims to reduce these artifacts by modifying the susceptible edge boundaries to create small, unnoticeable overlaps between the color planes. We propose three low-complexity algorithms for automatic color trapping which hide the effects of small color plane mis-registrations. Our algorithms are designed for software or embedded firmware implementation. The trapping method they follow is based on a hardware-friendly technique proposed by J. Trask (JTHBCT03) which is too computationally expensive for software or firmware implementation. The first two algorithms are based on the use of look-up tables (LUTs). The first LUT-based algorithm corrects all registration errors of one pixel in extent and reduces several cases of misregistration errors of two pixels in extent using only 727 Kbytes of storage space. This algorithm is particularly attractive for implementation in the embedded firmware of low-cost formatter-based printers. The second LUT-based algorithm corrects all types of misregistration errors of up to two pixels in extent using 3.7 Mbytes of storage space. The third algorithm is a hybrid one that combines LUTs and feature extraction to minimize the storage requirements (724 Kbytes) while still correcting all misregistration errors of up to two pixels in extent. This algorithm is suitable for both embedded firmware implementation on low-cost formatter-based printers and software implementation on host-based printers.

A Hand-Held Multimedia Translation and Interpretation System with Application to Diet Management

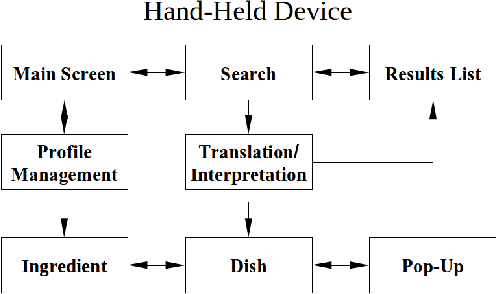
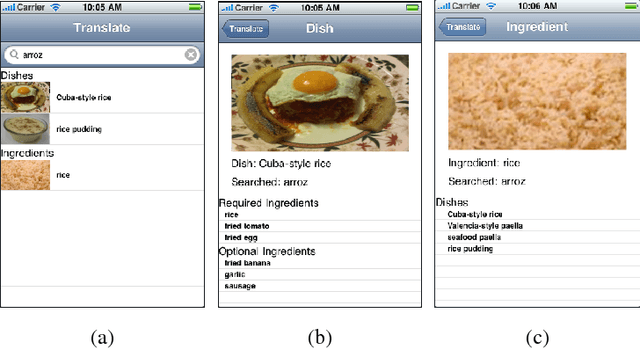
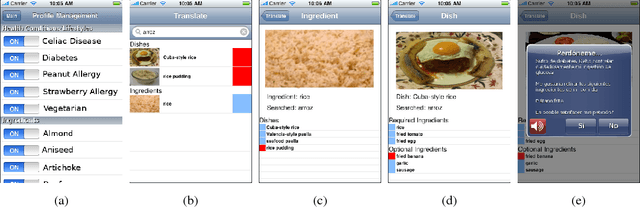
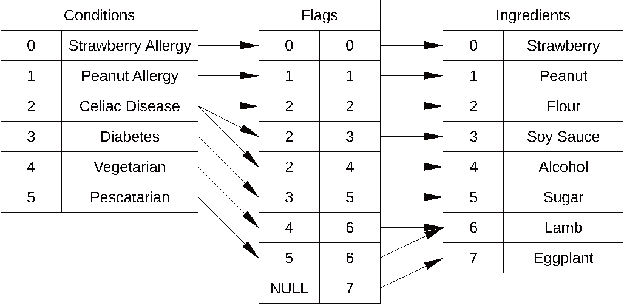
We propose a network independent, hand-held system to translate and disambiguate foreign restaurant menu items in real-time. The system is based on the use of a portable multimedia device, such as a smartphones or a PDA. An accurate and fast translation is obtained using a Machine Translation engine and a context-specific corpora to which we apply two pre-processing steps, called translation standardization and $n$-gram consolidation. The phrase-table generated is orders of magnitude lighter than the ones commonly used in market applications, thus making translations computationally less expensive, and decreasing the battery usage. Translation ambiguities are mitigated using multimedia information including images of dishes and ingredients, along with ingredient lists. We implemented a prototype of our system on an iPod Touch Second Generation for English speakers traveling in Spain. Our tests indicate that our translation method yields higher accuracy than translation engines such as Google Translate, and does so almost instantaneously. The memory requirements of the application, including the database of images, are also well within the limits of the device. By combining it with a database of nutritional information, our proposed system can be used to help individuals who follow a medical diet maintain this diet while traveling.