Path Tracking using Echoes in an Unknown Environment: the Issue of Symmetries and How to Break Them

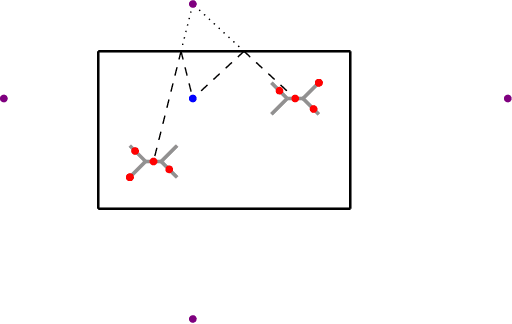
This paper deals with the problem of reconstructing the path of a vehicle in an unknown environment consisting of planar structures using sound. Many systems in the literature do this by using a loudspeaker and microphones mounted on a vehicle. Symmetries in the environment lead to solution ambiguities for such systems. We propose to resolve this issue by placing the loudspeaker at a fixed location in the environment rather than on the vehicle. The question of whether this will remove ambiguities regardless of the environment geometry leads to a question about breaking symmetries that can be phrased in purely mathematical terms. We solve this question in the affirmative if the geometry is in dimension three or bigger, and give counterexamples in dimension two. Excluding the rare situations where the counterexamples arise, we also give an affirmative answer in dimension two. Our results lead to a simple path reconstruction algorithm for a vehicle carrying four microphones navigating within an environment in which a loudspeaker at a fixed position emits short bursts of sounds. This algorithm could be combined with other methods from the literature to construct a path tracking system for vehicles navigating within a potentially symmetric environment.

Global Positioning: the Uniqueness Question and a New Solution Method

We provide a new algebraic solution procedure for the global positioning problem in $n$ dimensions using $m$ satellites. We also give a geometric characterization of the situations in which the problem does not have a unique solution. This characterization shows that such cases can happen in any dimension and with any number of satellites, leading to counterexamples to some open conjectures. We fill a gap in the literature by giving a proof for the long-held belief that when $m \ge n+2$, the solution is unique for almost all user positions. Even better, when $m \ge 2n+2$, almost all satellite configurations will guarantee a unique solution for all user positions. Some of our results are obtained using tools from algebraic geometry.

Multilateration and Signal Matching with Unknown Emission Times

Assume that a source emits a signal in $3$-dimensional space at an unknown time, which is received by at least~$5$ sensors. In almost all cases the emission time and source position can be worked out uniquely from the knowledge of the times when the sensors receive the signal. The task to do so is the multilateration problem. But when there are several emission events originating from several sources, the received signals must first be matched in order to find the emission times and source positions. In this paper, we propose to use algebraic relations between reception times to achieve this matching. A special case occurs when the signals are actually echoes from a single emission event. In this case, solving the signal matching problem allows one to reconstruct the positions of the reflecting walls. We show that, no matter where the walls are situated, our matching algorithm works correctly for almost all positions of the sensors. In the first section of this paper we consider the multilateration problem, which is equivalent to the GPS-problem, and give a simple algebraic solution that applies in all dimensions.

Can a Ground-Based Vehicle Hear the Shape of a Room?

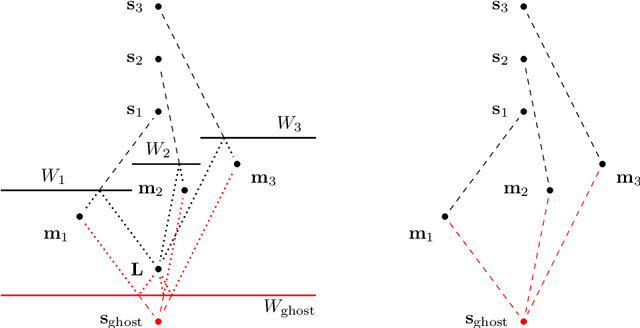
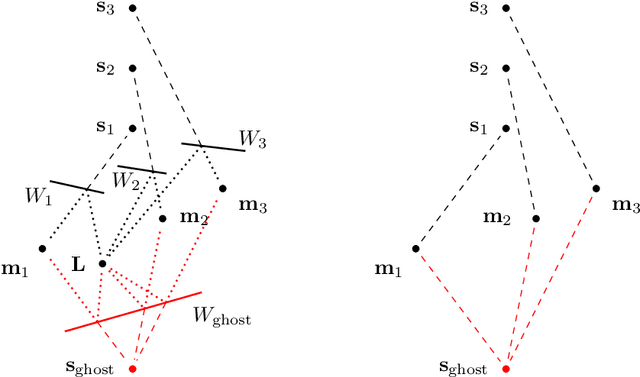
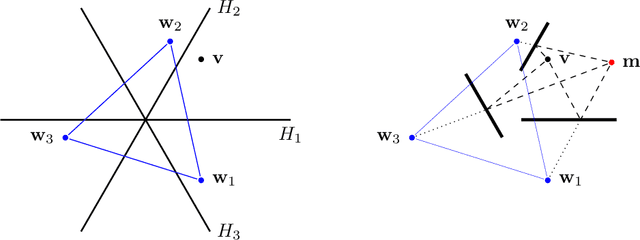
Assume that a ground-based vehicle moves in a room with walls or other planar surfaces. Can the vehicle reconstruct the positions of the walls from the echoes of a single sound event? We assume that the vehicle carries some microphones and that a loudspeaker is either also mounted on the vehicle or placed at a fixed location in the room. We prove that the reconstruction is almost always possible if (1) no echoes are received from floors, ceilings or sloping walls and the vehicle carries at least three non-collinear microphones, or if (2) walls of any inclination may occur, the loudspeaker is fixed in the room and there are four non-coplanar microphones. The difficulty lies in the echo-matching problem: how to determine which echoes come from the same wall. We solve this by using a Cayley-Menger determinant. Our proofs use methods from computational commutative algebra.

Lossless Representation of Graphs using Distributions

We consider complete graphs with edge weights and/or node weights taking values in some set. In the first part of this paper, we show that a large number of graphs are completely determined, up to isomorphism, by the distribution of their sub-triangles. In the second part, we propose graph representations in terms of one-dimensional distributions (e.g., distribution of the node weights, sum of adjacent weights, etc.). For the case when the weights of the graph are real-valued vectors, we show that all graphs, except for a set of measure zero, are uniquely determined, up to isomorphism, from these distributions. The motivating application for this paper is the problem of browsing through large sets of graphs.

Which Point Configurations are Determined by the Distribution of their Pairwise Distances?

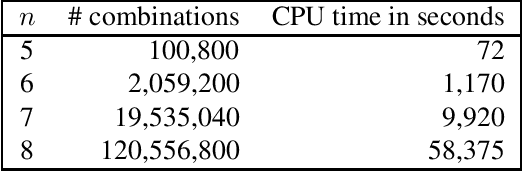
In a previous paper we showed that, for any $n \ge m+2$, most sets of $n$ points in $\RR^m$ are determined (up to rotations, reflections, translations and relabeling of the points) by the distribution of their pairwise distances. But there are some exceptional point configurations which are not reconstructible from the distribution of distances in the above sense. In this paper, we present a reconstructibility test with running time $O(n^{11})$. The cases of orientation preserving rigid motions (rotations and translations) and scalings are also discussed.

On reconstructing n-point configurations from the distribution of distances or areas

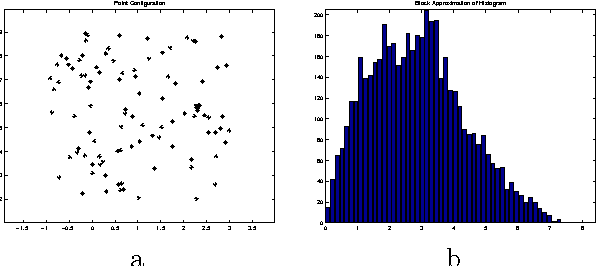
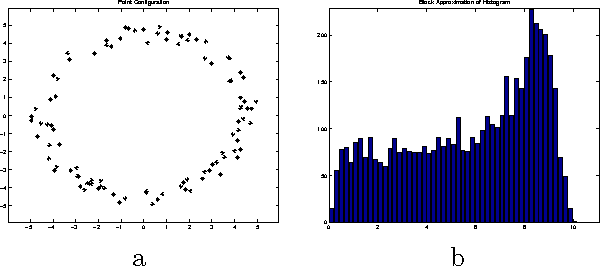
One way to characterize configurations of points up to congruence is by considering the distribution of all mutual distances between points. This paper deals with the question if point configurations are uniquely determined by this distribution. After giving some counterexamples, we prove that this is the case for the vast majority of configurations. In the second part of the paper, the distribution of areas of sub-triangles is used for characterizing point configurations. Again it turns out that most configurations are reconstructible from the distribution of areas, though there are counterexamples.