Which Point Configurations are Determined by the Distribution of their Pairwise Distances?
Paper and Code
Nov 02, 2003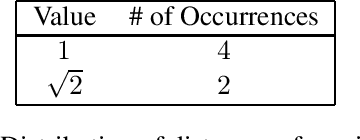
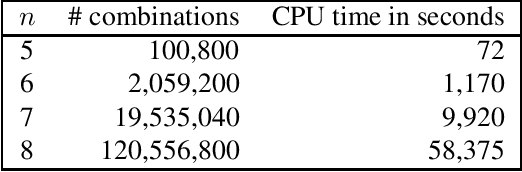
In a previous paper we showed that, for any $n \ge m+2$, most sets of $n$ points in $\RR^m$ are determined (up to rotations, reflections, translations and relabeling of the points) by the distribution of their pairwise distances. But there are some exceptional point configurations which are not reconstructible from the distribution of distances in the above sense. In this paper, we present a reconstructibility test with running time $O(n^{11})$. The cases of orientation preserving rigid motions (rotations and translations) and scalings are also discussed.
* 10 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge