Clustering small datasets in high-dimension by random projection

Datasets in high-dimension do not typically form clusters in their original space; the issue is worse when the number of points in the dataset is small. We propose a low-computation method to find statistically significant clustering structures in a small dataset. The method proceeds by projecting the data on a random line and seeking binary clusterings in the resulting one-dimensional data. Non-linear separations are obtained by extending the feature space using monomials of higher degrees in the original features. The statistical validity of the clustering structures obtained is tested in the projected one-dimensional space, thus bypassing the challenge of statistical validation in high-dimension. Projecting on a random line is an extreme dimension reduction technique that has previously been used successfully as part of a hierarchical clustering method for high-dimensional data. Our experiments show that with this simplified framework, statistically significant clustering structures can be found with as few as 100-200 points, depending on the dataset. The different structures uncovered are found to persist as more points are added to the dataset.

Pattern Dependence Detection using n-TARP Clustering

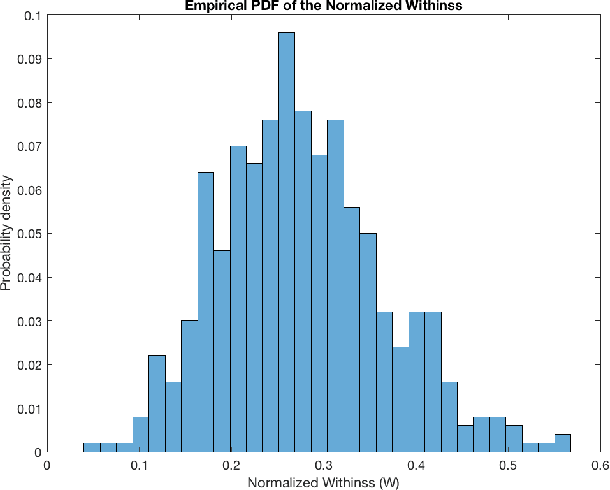
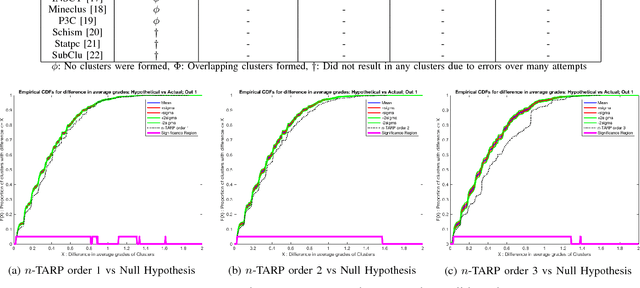
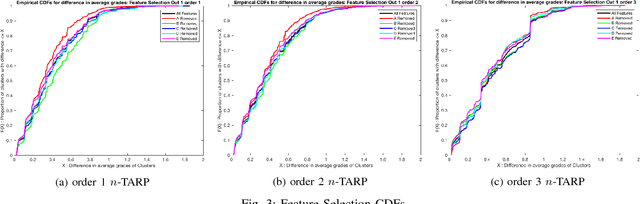
Consider an experiment involving a potentially small number of subjects. Some random variables are observed on each subject: a high-dimensional one called the "observed" random variable, and a one-dimensional one called the "outcome" random variable. We are interested in the dependencies between the observed random variable and the outcome random variable. We propose a method to quantify and validate the dependencies of the outcome random variable on the various patterns contained in the observed random variable. Different degrees of relationship are explored (linear, quadratic, cubic, ...). This work is motivated by the need to analyze educational data, which often involves high-dimensional data representing a small number of students. Thus our implementation is designed for a small number of subjects; however, it can be easily modified to handle a very large dataset. As an illustration, the proposed method is used to study the influence of certain skills on the course grade of students in a signal processing class. A valid dependency of the grade on the different skill patterns is observed in the data.

Benchmarks for Image Classification and Other High-dimensional Pattern Recognition Problems

A good classification method should yield more accurate results than simple heuristics. But there are classification problems, especially high-dimensional ones like the ones based on image/video data, for which simple heuristics can work quite accurately; the structure of the data in such problems is easy to uncover without any sophisticated or computationally expensive method. On the other hand, some problems have a structure that can only be found with sophisticated pattern recognition methods. We are interested in quantifying the difficulty of a given high-dimensional pattern recognition problem. We consider the case where the patterns come from two pre-determined classes and where the objects are represented by points in a high-dimensional vector space. However, the framework we propose is extendable to an arbitrarily large number of classes. We propose classification benchmarks based on simple random projection heuristics. Our benchmarks are 2D curves parameterized by the classification error and computational cost of these simple heuristics. Each curve divides the plane into a "positive- gain" and a "negative-gain" region. The latter contains methods that are ill-suited for the given classification problem. The former is divided into two by the curve asymptote; methods that lie in the small region under the curve but right of the asymptote merely provide a computational gain but no structural advantage over the random heuristics. We prove that the curve asymptotes are optimal (i.e. at Bayes error) in some cases, and thus no sophisticated method can provide a structural advantage over the random heuristics. Such classification problems, an example of which we present in our numerical experiments, provide poor ground for testing new pattern classification methods.