Parameterized TDOA: Instantaneous TDOA Estimation and Localization for Mobile Targets in a Time-Division Broadcast Positioning System

Localization of mobile targets is a fundamental problem across various domains. One-way ranging-based downlink localization has gained significant attention due to its ability to support an unlimited number of targets and enable autonomous navigation by performing localization at the target side. Time-difference-of-arrival (TDOA)-based methods are particularly advantageous as they obviate the need for target-anchor synchronization, unlike time-of-arrival (TOA)-based approaches. However, existing TDOA estimation methods inherently rely on the quasi-static assumption (QSA), which assumes that targets remain stationary during the measurement period, thereby limiting their applicability in dynamic environments. In this paper, we propose a novel instantaneous TDOA estimation method for dynamic environments, termed Parameterized TDOA (P-TDOA). We first characterize the nonlinear, time-varying TDOA measurements using polynomial models and construct a system of linear equations for the model parameters through dedicated transformations, employing a novel successive time difference strategy (STDS). Subsequently, we solve the parameters with a weighted least squares (WLS) solution, thereby obtaining instantaneous TDOA estimates. Furthermore, we develop a mobile target localization approach that leverages instantaneous TDOA estimates from multiple anchor pairs at the same instant. Theoretical analysis shows that our proposed method can approach the Cramer-Rao lower bound (CRLB) of instantaneous TDOA estimation and localization in concurrent TOA scenarios, despite actual TOA measurements being obtained sequentially. Extensive numerical simulations validate our theoretical analysis and demonstrate the effectiveness of the proposed method, highlighting its superiority over state-of-the-art approaches across various scenarios.

Efficient Rigid Body Localization based on Euclidean Distance Matrix Completion for AGV Positioning under Harsh Environment

In real-world applications for automatic guided vehicle (AGV) navigation, the positioning system based on the time-of-flight (TOF) measurements between anchors and tags is confronted with the problem of insufficient measurements caused by blockages to radio signals or lasers, etc. Mounting multiple tags at different positions of the AGV to collect more TOFs is a feasible solution to tackle this difficulty. Vehicle localization by exploiting the measurements between multiple tags and anchors is a rigid body localization (RBL) problem, which estimates both the position and attitude of the vehicle. However, the state-of-the-art solutions to the RBL problem do not deal with missing measurements, and thus will result in degraded localization availability and accuracy in harsh environments. In this paper, different from these existing solutions for RBL, we model this problem as a sensor network localization problem with missing TOFs. To solve this problem, we propose a new efficient RBL solution based on Euclidean distance matrix (EDM) completion, abbreviated as ERBL-EDMC. Firstly, we develop a method to determine the upper and lower bounds of the missing measurements to complete the EDM reliably, using the known relative positions between tags and the statistics of the TOF measurements. Then, based on the completed EDM, the global tag positions are obtained from a coarse estimation followed by a refinement step assisted with inter-tag distances. Finally, the optimal vehicle position and attitude are obtained iteratively based on the estimated tag positions from the previous step. Theoretical analysis and simulation results show that the proposed ERBL-EDMC method effectively solves the RBL problem with incomplete measurements. It obtains the optimal positioning results while maintaining low computational complexity compared with the existing RBL methods based on semi-definite relaxation.

A priori knowledge-free fast positioning approach for BeiDou receivers

A Global Navigation Satellite System (GNSS) receiver usually needs a sufficient number of full pseudorange measurements to obtain a position solution. However, it is time-consuming to acquire full pseudorange information from only the satellite broadcast signals due to the navigation data features of GNSS. In order to realize fast positioning during a cold or warm start in a GNSS receiver, the existing approaches require an initial estimation of position and time or require a number of computational steps to recover the full pseudorange information from fractional pseudoranges and then compute the position solution. The BeiDou Navigation Satellite System (BDS) has a unique constellation distribution and a fast navigation data rate for geostationary earth orbit (GEO) satellites. Taking advantage of these features, we propose a fast positioning technique for BDS receivers. It simultaneously processes the full and fractional pseudorange measurements from the BDS GEOs and non-GEOs, respectively, which is faster than processing all full measurements. This method resolves the position solution and recovers the full pseudoranges for non-GEOs simultaneously within 1 s theoretically and does not need an estimate of the initial position. Simulation and real data experiments confirm that the proposed technique completes fast positioning without a priori position and time estimation, and the positioning accuracy is identical with the conventional single-point positioning approach using full pseudorange measurements from all available satellites.

Robust Vehicle Positioning based on Multi-Epoch and Multi-Antenna TOAs in Harsh Environments

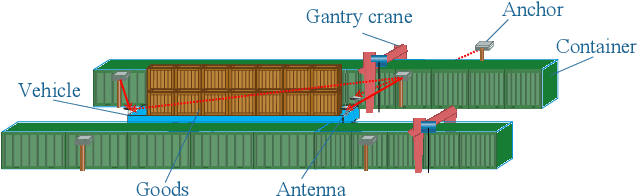
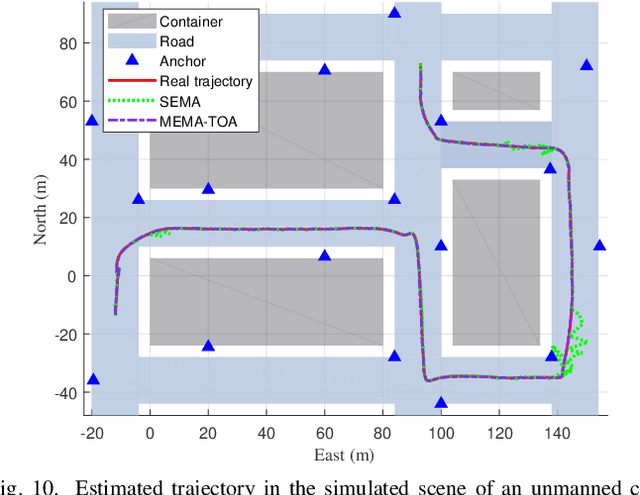
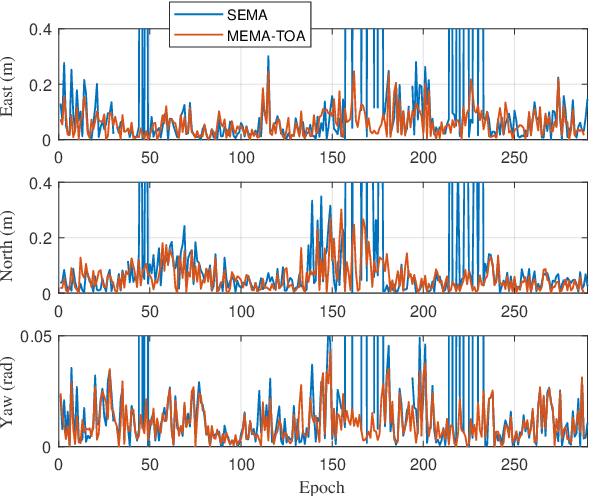
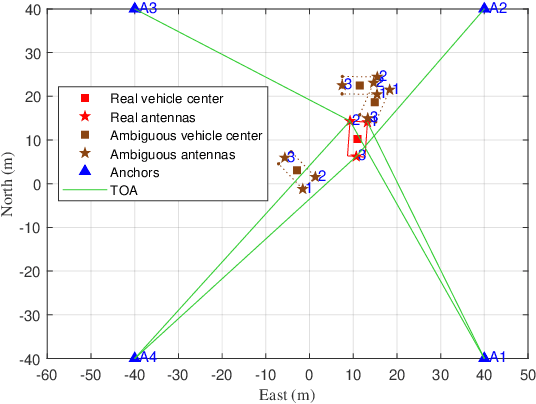
For radio-based time-of-arrival (TOA) positioning systems applied in harsh environments, obstacles in the surroundings and on the vehicle itself will block the signals from the anchors, reduce the number of available TOA measurements and thus degrade the localization performance. Conventional multi-antenna positioning technique requires a good initialization to avoid local minima, and suffers from location ambiguity due to insufficient number of TOA measurements and/or poor geometry of anchors at a single epoch. A new initialization method based on semidefinite programming (SDP), namely MEMA-SDP, is first designed to address the initialization problem of the MEMA-TOA method. Then, an iterative refinement step is developed to obtain the optimal positioning result based on the MEMA-SDP initialization. We derive the Cramer-Rao lower bound (CRLB) to analyze the accuracy of the new MEMA-TOA method theoretically, and show its superior positioning performance over the conventional single-epoch and multi-antenna (SEMA) localization method. Simulation results in harsh environments demonstrate that i) the new MEMA-SDP provides an initial estimation that is close to the real location, and empirically guarantees the global optimality of the final refined positioning solution, and ii) compared with the conventional SEMA method, the new MEMA-TOA method has higher positioning accuracy without location ambiguity, consistent with the theoretical analysis.

Sequential Doppler Shift based Optimal Localization and Synchronization with TOA

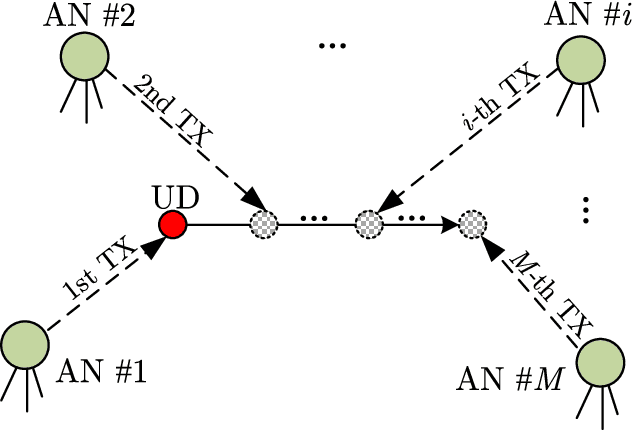
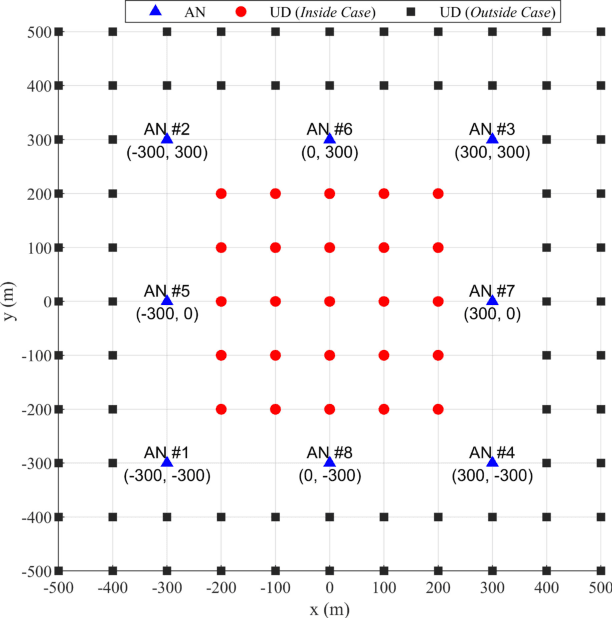
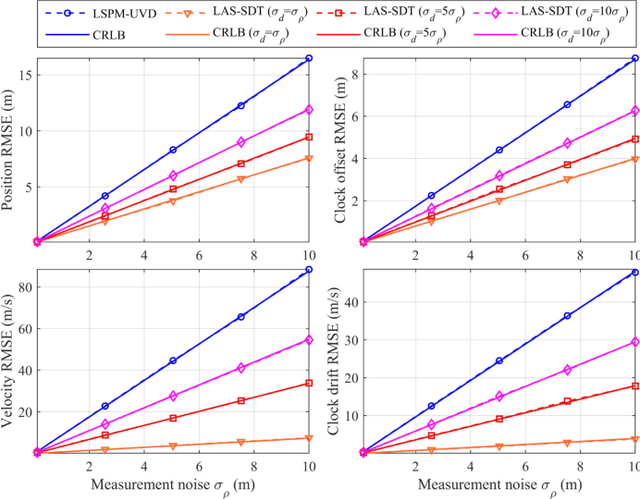
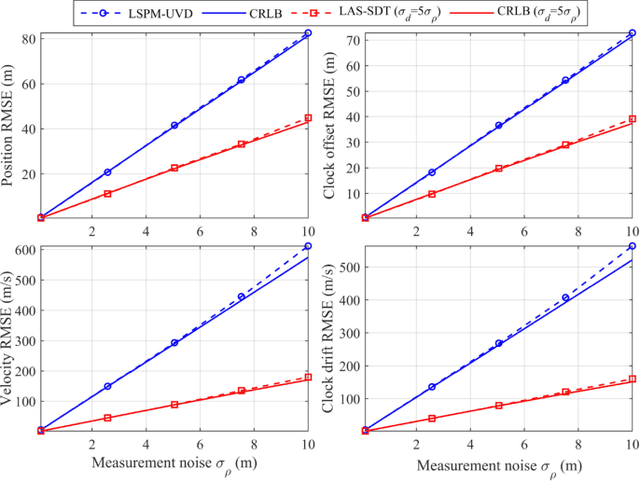
Doppler shift is an important measurement for localization and synchronization (LAS), and is available in various practical systems. Existing studies on LAS techniques in a time division broadcast LAS system (TDBS) only use sequential time-of-arrival (TOA) measurements from the broadcast signals. In this paper, we develop a new optimal LAS method in the TDBS, namely LAS-SDT, by taking advantage of the sequential Doppler shift and TOA measurements. It achieves higher accuracy compared with the conventional TOA-only method for user devices (UDs) with motion and clock drift. Another two variant methods, LAS-SDT-v for the case with UD velocity aiding, and LAS-SDT-k for the case with UD clock drift aiding, are developed. We derive the Cramer-Rao lower bound (CRLB) for these different cases. We show analytically that the accuracies of the estimated UD position, clock offset, velocity and clock drift are all significantly higher than those of the conventional LAS method using TOAs only. Numerical results corroborate the theoretical analysis and show the optimal estimation performance of the LAS-SDT.

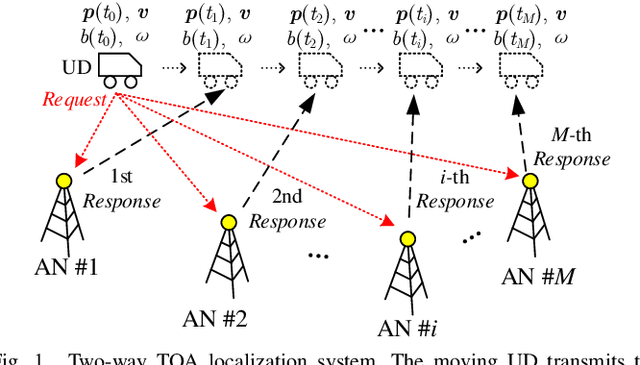
Closed-form Two-way TOA Localization and Synchronization for User Devices with Motion and Clock Drift

A two-way time-of-arrival (TOA system is composed of anchor nodes (ANs and user devices (UDs . Two-way TOA measurements between AN-UD pairs are obtained via round-trip communications to achieve localization and synchronization (LAS for a UD. Existing LAS method for a moving UD with clock drift adopts an iterative algorithm, which requires accurate initialization and has high computational complexity. In this paper, we propose a new closed-form two-way TOA LAS approach, namely CFTWLAS, which does not require initialization, has low complexity and empirically achieves optimal LAS accuracy. We first linearize the LAS problem by squaring and differencing the two-way TOA equations. We employ two auxiliary variables to simplify the problem to finding the analytical solution of quadratic equations. Due to the measurement noise, we can only obtain a raw LAS estimation from the solution of the auxiliary variables. Then, a weighted least squares step is applied to further refine the raw estimation. We analyze the theoretical error of the new CFTWLAS and show that it empirically reaches the Cramer-Rao lower bound (CRLB with sufficient ANs under the condition with proper geometry and small noise. Numerical results in a 3D scenario verify the theoretical analysis that the estimation accuracy of the new CFTWLAS method reaches CRLB in the presented experiments when the number of the ANs is large, the geometry is appropriate, and the noise is small. Unlike the iterative method whose complexity increases with the iteration count, the new CFTWLAS has constant low complexity.

Sequential TOA-Based Moving Target Localization in Multi-Agent Networks

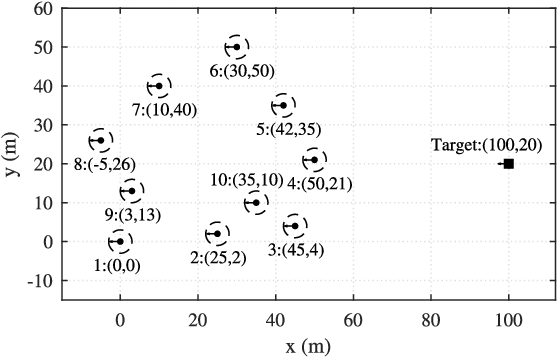
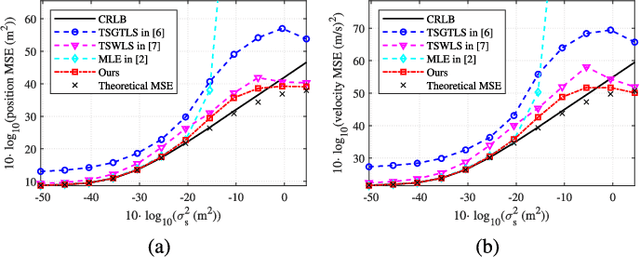
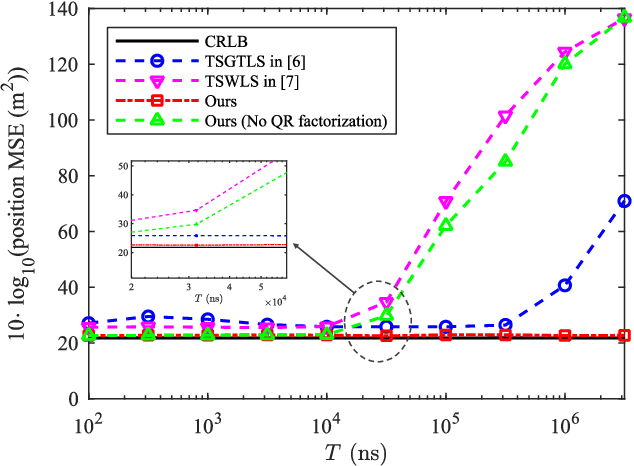
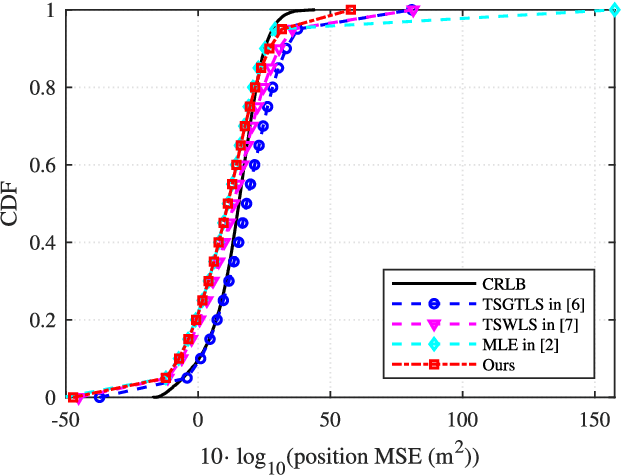
Localizing moving targets in unknown harsh environments has always been a severe challenge. This letter investigates a novel localization system based on multi-agent networks, where multiple agents serve as mobile anchors broadcasting their time-space information to the targets. We study how the moving target can localize itself using the sequential time of arrival (TOA) of the one-way broadcast signals. An extended two-step weighted least squares (TSWLS) method is proposed to jointly estimate the position and velocity of the target in the presence of agent information uncertainties. We also address the large target clock offset (LTCO) problem for numerical stability. Analytical results reveal that our method reaches the Cramer-Rao lower bound (CRLB) under small noises. Numerical results show that the proposed method performs better than the existing algorithms.

A New TOA Localization and Synchronization System with Virtually Synchronized Periodic Asymmetric Ranging Network

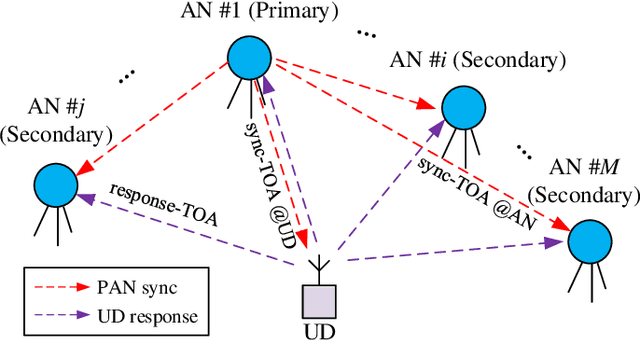
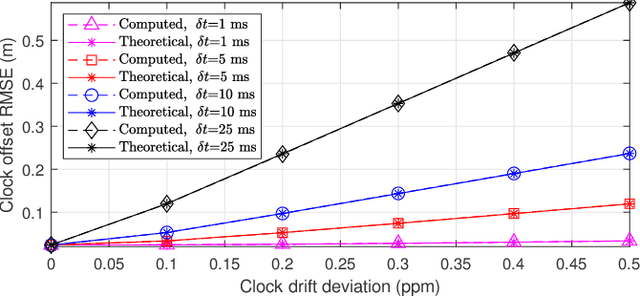
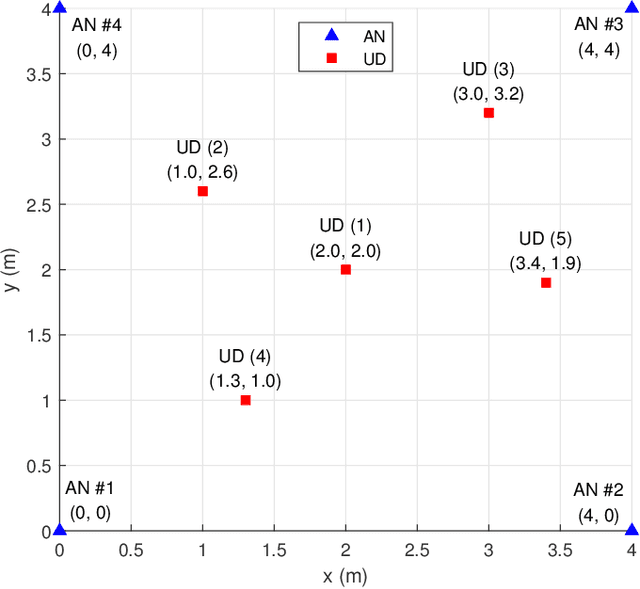
In this article, we design a new time-of-arrival (TOA) system for simultaneous user device (UD) localization and synchronization with a periodic asymmetric ranging network, namely PARN. The PARN includes one primary anchor node (PAN) transmitting and receiving signals, and many secondary ANs (SAN) only receiving signals. All the UDs can transmit and receive signals. The PAN periodically transmits sync signal and the UD transmits response signal after reception of the sync signal. Using TOA measurements from the periodic sync signal at SANs, we develop a Kalman filtering method to virtually synchronize ANs with high accuracy estimation of clock parameters. Employing the virtual synchronization, and TOA measurements from the response signal and sync signal, we then develop a maximum likelihood (ML) approach, namely ML-LAS, to simultaneously localize and synchronize a moving UD. We analyze the UD localization and synchronization error, and derive the Cramer-Rao lower bound (CRLB). Different from existing asymmetric ranging network-based TOA systems, the new PARN i) uses the periodic sync signals at the SAN to exploit the temporal correlated clock information for high accuracy virtual synchronization, and ii) compensates the UD movement and clock drift using various TOA measurements to achieve consistent and simultaneous localization and synchronization performance. Numerical results verify the theoretical analysis that the new system has high accuracy in AN clock offset estimation and simultaneous localization and synchronization for a moving UD. We implement a prototype hardware system and demonstrate the feasibility and superiority of the PARN in real-world applications by experiments.

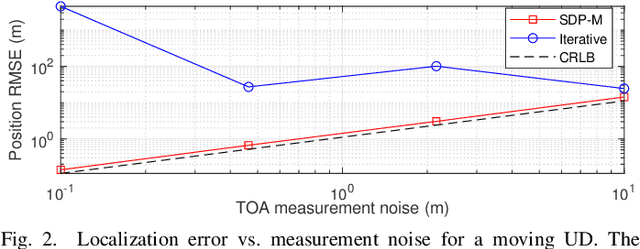
Semidefinite Programming Two-way TOA Localization for User Devices with Motion and Clock Drift

In two-way time-of-arrival (TOA) systems, a user device (UD) obtains its position by round-trip communications to a number of anchor nodes (ANs) at known locations. The objective function of the maximum likelihood (ML) method for two-way TOA localization is nonconvex. Thus, the widely-adopted Gauss-Newton iterative method to solve the ML estimator usually suffers from the local minima problem. In this paper, we convert the original estimator into a convex problem by relaxation, and develop a new semidefinite programming (SDP) based localization method for moving UDs, namely SDP-M. Numerical result demonstrates that compared with the iterative method, which often fall into local minima, the SDP-M always converge to the global optimal solution and significantly reduces the localization error by more than 40%. It also has stable localization accuracy regardless of the UD movement, and outperforms the conventional method for stationary UDs, which has larger error with growing UD velocity.

Optimal Localization with Sequential Pseudorange Measurements for Moving Users in a Time Division Broadcast Positioning System

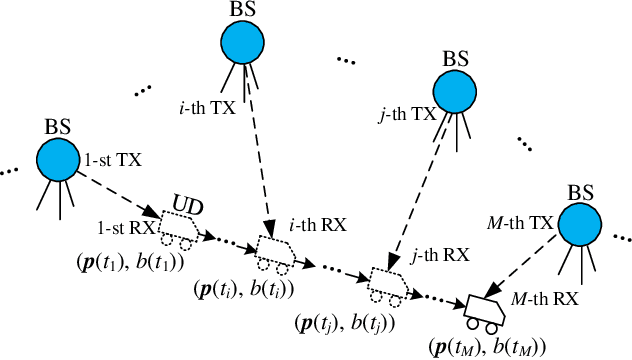
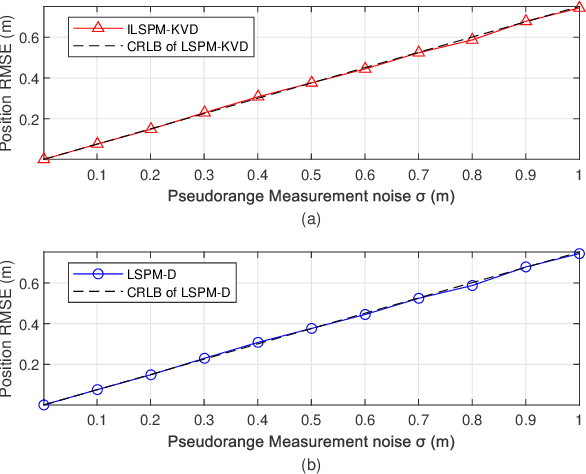
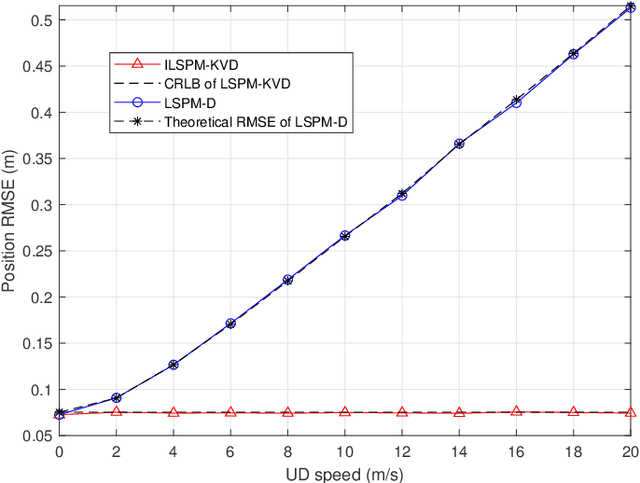
In a time division broadcast positioning system (TDBPS), a user device (UD) determines its position by obtaining sequential time-of-arrival (TOA) or pseudorange measurements from signals broadcast by multiple synchronized base stations (BSs). The existing localization method using sequential pseudorange measurements and a linear clock drift model for the TDPBS, namely LSPM-D, does not compensate the position displacement caused by the UD movement and will result in position error. In this paper, depending on the knowledge of the UD velocity, we develop a set of optimal localization methods for different cases. First, for known UD velocity, we develop the optimal localization method, namely LSPM-KVD, to compensate the movement-caused position error. We show that the LSPM-D is a special case of the LSPM-KVD when the UD is stationary with zero velocity. Second, for the case with unknown UD velocity, we develop a maximum likelihood (ML) method to jointly estimate the UD position and velocity, namely LSPM-UVD. Third, in the case that we have prior distribution information of the UD velocity, we present a maximum a posteriori (MAP) estimator for localization, namely LSPM-PVD. We derive the Cramer-Rao lower bound (CRLB) for all three estimators and analyze their localization error performance. We show that the position error of the LSPM-KVD increases as the assumed known velocity deviates from the true value. As expected, the LSPM-KVD has the smallest position error while the LSPM-PVD and the LSPM-UVD are more robust when the prior knowledge of the UD velocity is limited. Numerical results verify the theoretical analysis on the optimality and the positioning accuracy of the proposed methods.